1.随机链表的逻辑结构复制
原题链接:
. - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode-cn.com/problems/copy-list-with-random-pointer/description/ 据说做这道题,能把思路想明白,并且能把思路转化为代码,那说明单链表掌握水平就有八成的功力了。
https://leetcode-cn.com/problems/copy-list-with-random-pointer/description/ 据说做这道题,能把思路想明白,并且能把思路转化为代码,那说明单链表掌握水平就有八成的功力了。
这道题如果只是复制一份链表,那还是简单的,麻烦的地方在于,让新链表结点成员“random”与原来的链表逻辑地址相符。此处会有三个坑:
坑1:如果原封不动的把random抄过来,会变成下面这副模样,新节点的random指着原来的链表。
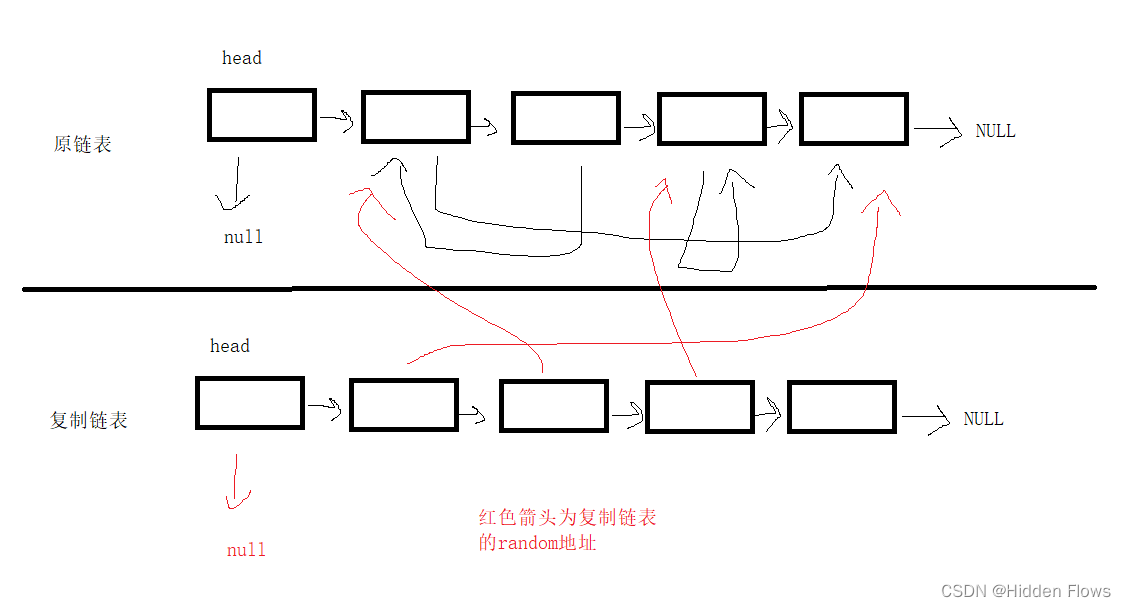
坑2:如果根据结点的val值来确定random指向的是谁,会出现下面的情况,遇到相同val值出错:

坑3:如果先记下每个节点的random指向的是第几个节点,之后再根据记下的位置给复制的结点的random赋值,这样做虽然可以,但是时间复杂度过高:N(n^2),得遍历每一个结点并通过遍历找到每个结点指向的结点是第几个。
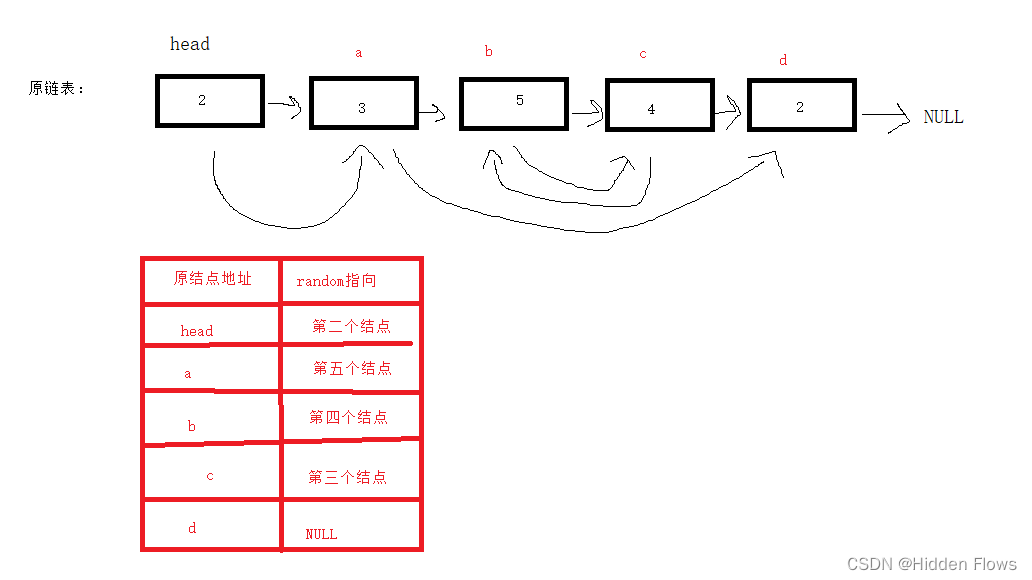
问题的关键在于,我们需要一个东西来帮我们记住指向的结点是第几个,依靠暴力统计是不合理的,唯一剩下的能表达位置关系的只有原链表本身,那我们我们该怎么利用呢?
让新链表长在旧链表上:
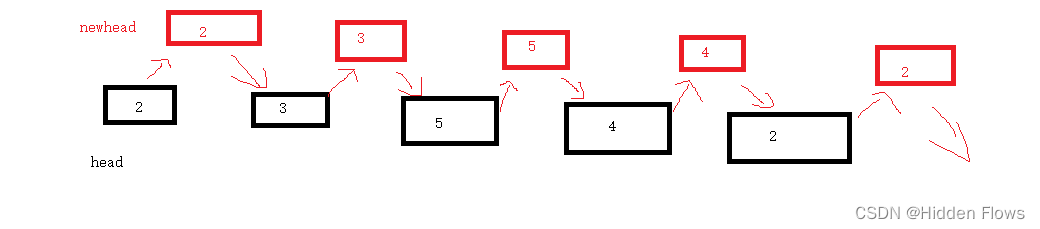
如图所示,在原链表每个结点后面插入复制的新结点,这样做的好处是,我们可以方便的确定新结点的random:原理如下

思路解决了,总的代码如下:
// 创建新节点
struct Node* createNode(int val) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
if (newNode == NULL) {
printf("Memory allocation failed\n");
exit(0);
}
newNode->val = val;
newNode->next = NULL;
newNode->random = NULL;
return newNode;
}
// 拷贝链表函数
struct Node* copyRandomList(struct Node* head) {
if (head == NULL) return NULL;
// 第一步:在每个原节点旁边创建新节点,新节点的next指向下一个原节点
struct Node* current = head;
while (current != NULL) {
struct Node* newNode = createNode(current->val);
newNode->next = current->next;
current->next = newNode;
current = newNode->next;
}
// 第二步:根据原节点的random指针设置新节点的random指针
current = head;
while (current != NULL) {
if (current->random != NULL) {
current->next->random = current->random->next;
}
current = current->next->next;
}
// 第三步:拆分链表
struct Node* newHead = head->next;
struct Node* newCurrent = newHead;
current = head;
while (current != NULL) {
current->next = newCurrent->next;
if (current->next != NULL) {
newCurrent->next = current->next->next;
}
current = current->next;
newCurrent = newCurrent->next;
}
return newHead;
}这里解释一下为什么不在创建结点的阶段就把random确定好:原因1是没有创建后面的结点是不能知道应该指向哪里的,原因2是哪怕只是为了取巧通过考试测试用例,也会有错误:

假设原来的第三个结点指向了第五个结点,如果边创建新结点边给random赋值,按照之前的思路,他指向的random的情况会是这样的:
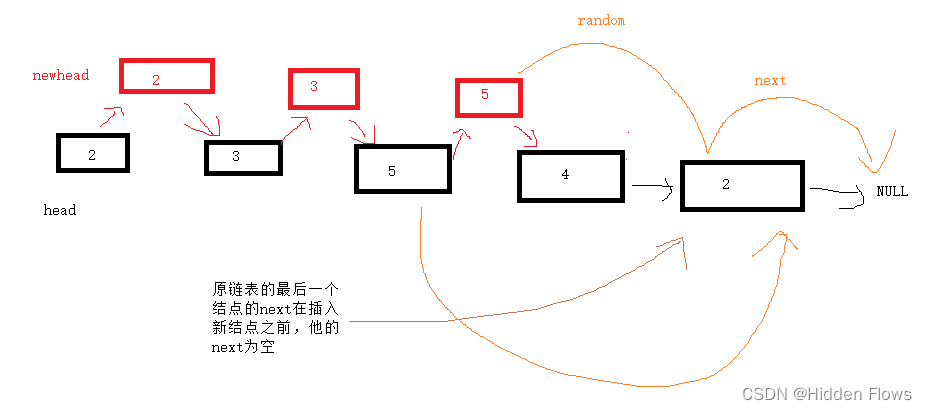
他指向了不该指向的NULL;
2.带环链表找入口
原题链接:
. - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode-cn.com/problems/linked-list-cycle-ii/description/首先我们需要判断链表是否带环:
https://leetcode-cn.com/problems/linked-list-cycle-ii/description/首先我们需要判断链表是否带环:
建立一个快指针(一次走俩个结点)和一个慢指针(一次走一个结点),俩者从起点出发,如果中途相遇,则说明带环,若快指针next到了NULL,说明不带环。
由于快慢指针的相对速度是1(没走一次距离变化为1),所以不会出现错过的情况。
道理比较简单,实现方式如下:
bool hasCycle(struct ListNode *head) {
struct ListNode* fast = head,*slow = head;
while(fast&&fast->next)
{
fast = fast->next->next;
slow = slow->next;
if(slow == fast)
return true;
}
return false;
}注意fast一次走俩步,所以要判断fast和fast的下一个是不是NULL来确定是否到结尾。
此时我们可以顺手加一个变量n来记录慢指针行动的次数:之后会用他找相遇点,修改后的代码如下:
int hasCycle(struct ListNode *head) {
struct ListNode* fast = head,*slow = head;
int n = 0;//n是slow走的步数
while(fast&&fast->next)
{
fast = fast->next->next;
slow = slow->next;
n++;
if(slow == fast)
return n;
}
return -1;//跳出循环,说明不带环,-1表示不带环
}我们不用担心slow与fast相遇时,slow在环里转了很多圈,推理图如下:

我们通过前面的hasCycl函数可以得到去相遇点的步数,只需要让一个慢指针从head开始走n步就可以获取相遇点的地址了:
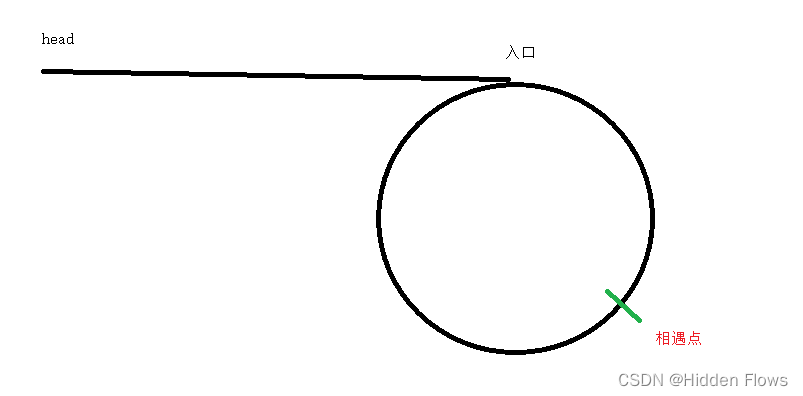
此时,如果定义俩个慢指针分别指向head和相遇点,让他们一次走一个结点,最后他们会在入口相遇,这个入口的地址就是这个题目需要的答案,这里解释一下为什么这么巧:

这道题思路解决后,代码实现是很简单的。