核函数
- ==**问题一:为什么说是有限维就一定存在高维空间可分呢?**==
- 原始空间与特征空间
- 为什么映射到高维空间可以实现可分
- 核函数的作用
- ==**问题二:最终怎么得到函数**==
- 从对偶问题到决策函数的步骤:
- 结论
- ==**问题三:为什么说特征空间的好坏对于SVM性能重要?和核函数有什么关系?**==
- 特征空间
- 核函数
- 特征空间的重要性
- 核函数与特征空间的关系
- 总结
- ==**问题四:半正定性理解**==
- 实际例子:
- ==**问题五:为什么函数组合也能最终成立?**==
- 1. 核函数的线性组合
- 2. 核函数的直积
- 3. 核函数与函数的乘积
- 总结
- 核函数讨论
- 常用核函数
- 使用核函数经验
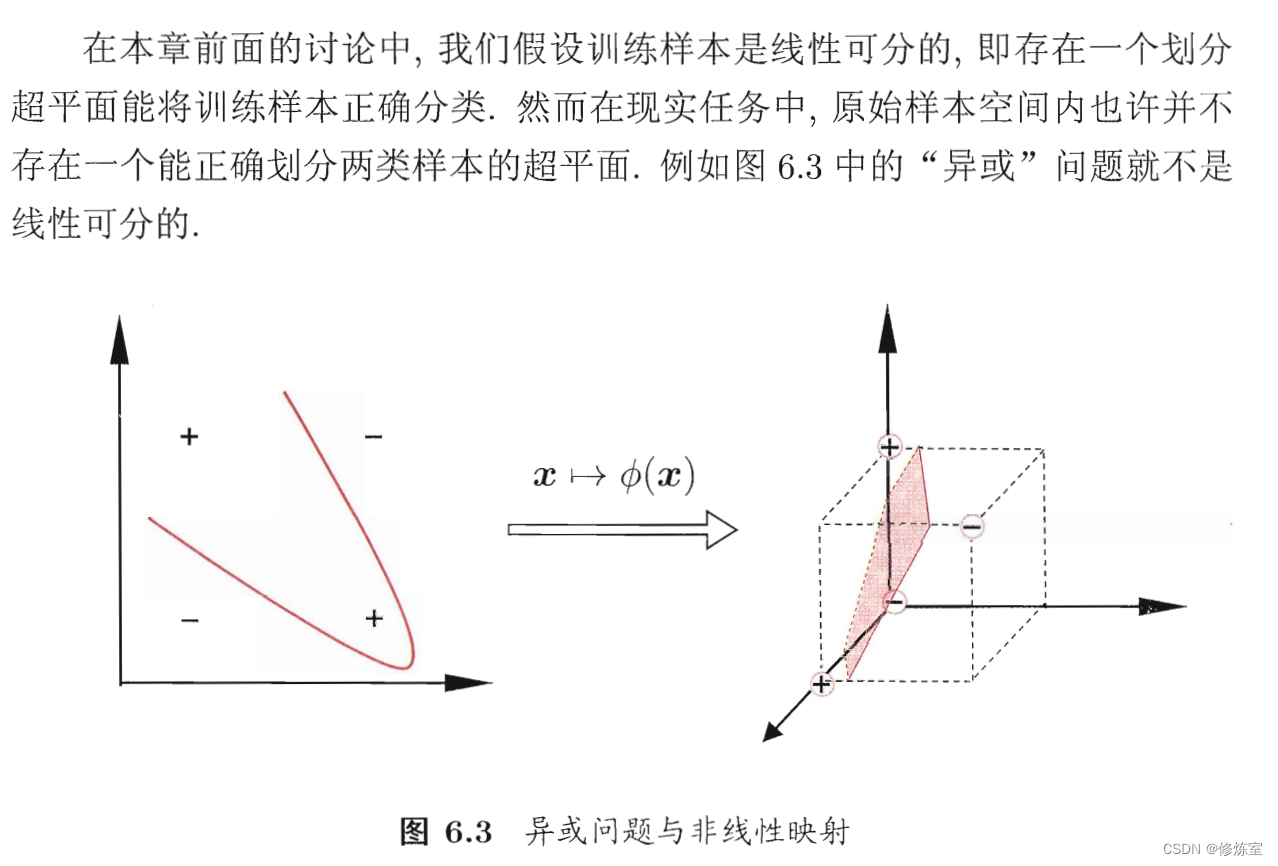
问题一:为什么说是有限维就一定存在高维空间可分呢?
这个问题触及了核函数和支持向量机(SVM)中的一个基本概念,即通过映射到高维空间来实现数据的线性可分。这个概念基于Cover定理,它暗示了一个非线性可分的数据集在高维空间中更可能是线性可分的。
原始空间与特征空间
首先,我们来区分两个概念:
- 原始空间:这是我们的数据所在的空间,通常由数据的
特征维度决定。 - 特征空间:这是通过某种映射(可能是非线性的)将原始数据转换后的空间,通常维度高于原始空间。
为什么映射到高维空间可以实现可分
-
Cover的定理:这个定理指出,对于非线性可分的数据,通过非线性映射到高维空间,可以使得数据在这个高维空间内变得线性可分。定理认为,如果原始空间是有限维的,且数据是
随机生成的,那么原始数据投影到足够高维的空间后,存在线性超平面能将数据正确分类的可能性会增加。 -
维度灾难:在低维空间中,数据点往往会
彼此挤压,但在高维空间中,每个点都可以“呼吸”,因为空间大得多,每个数据点间的相对距离可能增加,这有助于找到一个合适的线性分界来区分不同类别。 -
几何直觉:在二维空间中,我们可以用一条线来分隔点;在三维空间中,我们可以用一个平面来分隔点。随着维度的增加,我们可以使用更高维的“超平面”来分隔点集。在足够高的维度中,几乎总是可以找到一个超平面将数据集分隔成两部分。
-
特征组合:通过映射到高维空间,我们实际上在创建原始特征的各种非线性组合。例如,如果原始特征是 x 1 x_1 x1 和 x 2 x_2 x2,在高维空间中,我们可能有 x 1 2 x_1^2 x12、 x 1 x 2 x_1x_2 x1x2、 x 2 2 x_2^2 x22 等特征。这些新特征有时会揭示数据中隐藏的结构,这些结构在原始空间中不是线性可分的。
核函数的作用
核函数允许我们在 不显式计算 高维映射的情况下,通过在原始空间内进行内积运算来间接工作在这个高维特征空间内。这就是所谓的“核技巧”,它避免了直接在高维空间中的昂贵计算。

问题二:最终怎么得到函数

当我们使用核函数
k
(
⋅
,
⋅
)
k(\cdot, \cdot)
k(⋅,⋅) 在SVM中,我们实际上是在使用一个非线性映射
ϕ
\phi
ϕ 将原始特征空间映射到一个高维空间,在这个高维空间中,数据更有可能是线性可分的。在这个高维空间中,我们的目标函数和决策函数将基于这个映射来表达。让我们一步步分解这个过程,了解如何从对偶问题的目标函数得到最终的决策函数
f
(
x
)
f(x)
f(x)。
从对偶问题到决策函数的步骤:
-
对偶问题的目标函数:
在对偶问题中,我们最大化关于拉格朗日乘子 ( \alpha ) 的函数:
max α ( ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j k ( x i , x j ) ) \max_{\alpha} \left( \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j k(x_i, x_j) \right) αmax(i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjk(xi,xj))其中,约束条件是 ∑ i = 1 m α i y i = 0 \sum_{i=1}^{m} \alpha_i y_i = 0 ∑i=1mαiyi=0 且 α i ≥ 0 \alpha_i \geq 0 αi≥0。这个目标函数本质上是SVM原始问题的拉格朗日形式,其中的内积 x i T x j x_i^T x_j xiTxj 被核函数 k ( x i , x j ) k(x_i, x_j) k(xi,xj) 替代。
-
决策函数的构建:
一旦我们找到了最优的 α \alpha α 值,我们可以构建SVM的决策函数。在没有核函数的情况下,我们有 f ( x ) = w T x + b f(x) = w^T x + b f(x)=wTx+b。当使用核函数时, w w w 可以表示为:
w = ∑ i = 1 m α i y i ϕ ( x i ) w = \sum_{i=1}^{m} \alpha_i y_i \phi(x_i) w=i=1∑mαiyiϕ(xi)
w w w 现在是映射到高维空间的向量。我们无需直接计算 w w w,因为在核函数的帮助下,我们可以仅通过原始特征空间中的数据点来计算 w T ϕ ( x ) w^T \phi(x) wTϕ(x)。
-
核函数的应用:
核函数 k ( x i , x ) k(x_i, x) k(xi,x) 实际上是 ϕ ( x i ) \phi(x_i) ϕ(xi) 和 ϕ ( x ) \phi(x) ϕ(x) 的
内积ϕ ( x i ) T ϕ ( x ) \phi(x_i)^T \phi(x) ϕ(xi)Tϕ(x)。因此,决策函数 f ( x ) f(x) f(x) 可以重写为:
f ( x ) = ∑ i = 1 m α i y i k ( x , x i ) + b f(x) = \sum_{i=1}^{m} \alpha_i y_i k(x, x_i) + b f(x)=i=1∑mαiyik(x,xi)+b这里, k ( x , x i ) k(x, x_i) k(x,xi) 就是我们的核函数,它提供了一种有效的方式来计算在高维空间中 ϕ ( x ) \phi(x) ϕ(x) 与所有 ϕ ( x i ) \phi(x_i) ϕ(xi) 的内积,无需直接在高维空间中操作。
-
计算 ( b ):
为了找到偏置项 ( b ),我们可以使用任意一个支持向量 ( x_s )(即对应的 α s > 0 \alpha_s > 0 αs>0):
y s ( ∑ i = 1 m α i y i k ( x s , x i ) + b ) = 1 y_s \left( \sum_{i=1}^{m} \alpha_i y_i k(x_s, x_i) + b \right) = 1 ys(i=1∑mαiyik(xs,xi)+b)=1从上面的式子中解出 ( b )。通常我们会使用所有支持向量得到的 ( b ) 值的
平均值以获得更稳健的估计。 -
最终的决策函数:
最终的SVM决策函数在使用了核函数的情况下形式如下:
f ( x ) = ∑ i = 1 m α i y i k ( x , x i ) + b f(x) = \sum_{i=1}^{m} \alpha_i y_i k(x, x_i) + b f(x)=i=1∑mαiyik(x,xi)+b这个函数可以用来估计新样本 ( x ) 的类别标签。如果 f ( x ) > 0 f(x) > 0 f(x)>0,则 ( x ) 被分类为正类;如果 f ( x ) < 0 f(x) < 0 f(x)<0,则被分类为负类。
结论
核函数
k
(
x
i
,
x
j
)
k(x_i, x_j)
k(xi,xj) 的引入允许我们在原始特征空间中间接使用高维空间的内积。这个过程提供了一种有效的计算方式,即使在高维空间中也能够处理,这是通过将数据点映射到高维特征空间并计算它们之间的内积来实现。这个映射是隐式的,通过核函数
k
(
x
i
,
x
j
)
k(x_i, x_j)
k(xi,xj) 实现,无需显式地定义或计算映射
ϕ
\phi
ϕ。通过这种方式,我们能够构建决策函数来处理线性不可分的数据集。
问题三:为什么说特征空间的好坏对于SVM性能重要?和核函数有什么关系?

特征空间的质量对于SVM的性能至关重要,因为SVM是一个依赖于数据表示的机器学习模型。核函数在这里扮演了一个关键角色,因为它定义了在特征空间中如何度量样本之间的相似性。
特征空间
- 定义:特征空间是我们在其中构建模型的空间,由数据的
特征向量组成。 - 影响:数据在特征空间中的表示影响了模型的 学习能力 。如果特征能够很好地表示数据中的模式和关系,模型更容易学习。
核函数
- 映射:核函数隐式地将数据映射到一个更高维的特征空间中,帮助SVM在这个空间中找到线性分界面来分隔数据。
- 相似性度量:核函数实际上是在计算特征空间中两个向量的内积,这是一个 相似性的度量 。
- 选择:选择合适的核函数至关重要,因为它决定了数据如何在高维空间中被分布和区分。
特征空间的重要性
- 线性可分:在原始空间中不可分的数据,可以通过适当的映射在高维特征空间中变得线性可分。
- 模式识别:一个好的特征空间能更好地揭示数据中的模式,让SVM能够构建一个有效的分类器。
核函数与特征空间的关系
- 构造特征空间:核函数的选择直接定义了
特征空间的构造。例如,多项式核可以捕捉特征的各种组合,而高斯径向基函数(RBF)核可以度量点之间的“距离”,形成一个以 每个数据点为中心 的分布。 - 性能影响:一个不恰当的核函数可能导致特征空间中的样本点不适于线性分界,从而影响模型的准确度。
- 过拟合与泛化:合适的核函数可以帮助模型实现泛化,而不恰当的选择可能导致过拟合。
总结
在实践中,选择合适的核函数对于构建有效的SVM模型至关重要。它不仅影响模型对数据的理解和分界线的构建,也影响模型的泛化能力。通过使用核函数,SVM可以在复杂的数据集上找到简洁的决策规则,即便在原始特征空间中数据是高度非线性的。
问题四:半正定性理解
半正定性是高维空间中的一个重要概念,我们可以用一个简化的类比来帮助理解。
想象你有一座山,山顶是最高点。如果这座山的形状是凸的(像一个碗),那么无论你在山腰的哪个位置开始,都可以直接走最陡峭的路线到达山顶。在这座“凸山”上,无论你选择哪条路径,你总能达到山顶。这就像是一个半正定函数:不管你从哪个方向查看它,它总是“向上”的。
数学上,当我们谈论一个函数或矩阵的半正定性时,我们指的是一种类似的属性。一个半正定矩阵,当你用它来“量度”两个向量的相似性时,得到的结果总是非负的。这就保证了在我们通过这个矩阵来观察数据时,不会有意外的“洞”或者“下降”,只有平滑的“上升”或“平坦”。在核函数的背景下,这意味着无论我们选择什么样本点来计算它们的相似性,我们总会得到一个 合理的(非负的)值 。
实际例子:
假设我们有一个数据集包含两个点: x 1 x_1 x1 和 x 2 x_2 x2 。我们定义了一个简单的线性核函数 k ( x , z ) = x ⋅ z k(x, z) = x \cdot z k(x,z)=x⋅z ,即两个数的乘积。我们可以创建一个核矩阵 K K K 来表示这个数据集中所有点对的相似性:
K = [ x 1 ⋅ x 1 x 1 ⋅ x 2 x 2 ⋅ x 1 x 2 ⋅ x 2 ] K = \begin{bmatrix} x_1 \cdot x_1 & x_1 \cdot x_2 \\ x_2 \cdot x_1 & x_2 \cdot x_2 \end{bmatrix} K=[x1⋅x1x2⋅x1x1⋅x2x2⋅x2]
因为我们用点自身乘以自身,对角线上的值(
x
1
⋅
x
1
x_1 \cdot x_1
x1⋅x1 和
x
2
⋅
x
2
x_2 \cdot x_2
x2⋅x2)都是正的。如果
x
1
x_1
x1 和
x
2
x_2
x2 是正数,那么其他项也是正的,因此这个核矩阵是半正定的。这意味着,不管我们用这个矩阵来“测量”哪两个点的相似性,结果都不会是负的。
如果我们试图用这个核函数和矩阵来训练一个SVM,我们可以确定在优化过程中,不会出现任何数学上的意外。我们能够找到一个全局最优解,它将允许我们预测一个新点是否与数据集中的其他点相似。
通过确保我们的核矩阵是半正定的,我们就可以安心地使用它在高维空间中表示我们的数据,而不用担心在优化时会遇到数学上的问题。
问题五:为什么函数组合也能最终成立?

核函数的组合定理表明,我们可以通过已知的核函数来构建新的核函数。在SVM中,核函数用于隐式地映射数据到高维空间,从而允许在原始特征空间中找到非线性决策界面。如果
k
1
k_1
k1 和
k
2
k_2
k2 是两个有效的核函数(即分别对应于两个高维特征空间的内积),那么根据这些组合定理,我们可以创造出新的有效核函数,这些新的核函数仍然保持核函数所必须的数学属性。
1. 核函数的线性组合
如果 k 1 k_1 k1 和 k 2 k_2 k2 是核函数,那么对于任意的正系数 γ 1 \gamma_1 γ1 和 γ 2 \gamma_2 γ2,它们的线性组合 γ 1 k 1 + γ 2 k 2 \gamma_1 k_1 + \gamma_2 k_2 γ1k1+γ2k2 也是一个核函数。
- 原因:因为每个
k
i
k_i
ki 分别映射到一个RKHS,其
线性组合仍然映射到一个RKHS。在这个RKHS中,点积保留了所有原始点积的性质,并且线性组合也是半正定的,这是核函数必须满足的条件。
2. 核函数的直积
如果 k 1 k_1 k1 和 k 2 k_2 k2 是核函数,它们的直积 k 1 ⊗ k 2 k_1 \otimes k_2 k1⊗k2,定义为 k 1 ( x , z ) k 2 ( x , z ) k_1(x, z) k_2(x, z) k1(x,z)k2(x,z),也是一个核函数。
- 原因:直积实际上是在对应的RKHS中进行 点积操作 的
结果,它仍然满足半正定性。这意味着,如果我们在各自的空间中对两对向量取内积,然后将结果相乘,得到的仍然是所有向量的一个有效内积。
3. 核函数与函数的乘积
如果
k
1
k_1
k1 是核函数,
g
(
x
)
g(x)
g(x) 是一个函数,并且
g
(
x
)
g(x)
g(x) 在所考虑的定义域上是非负的,则
g
(
x
)
k
1
(
x
,
z
)
g
(
z
)
g(x) k_1(x, z) g(z)
g(x)k1(x,z)g(z) 也是一个核函数。
- 原因:这里
g
(
x
)
g(x)
g(x) 作为一个权重函数,它乘以
k
1
k_1
k1 不会破坏
k
1
k_1
k1 的半正定性质,因为
g
(
x
)
g(x)
g(x) 是非负的。所以
g
(
x
)
g(x)
g(x) 的作用可以被看作是在
k
1
k_1
k1 所对应的RKHS空间中对特征向量进行
缩放。
总结
核函数组合的正确性基于核函数必须满足的数学属性:它们必须对应于RKHS中的内积,并且核矩阵必须是半正定的。这些组合方法允许我们在保持这些属性的同时创造出新的核函数,给我们在特征空间的构造上提供了巨大的灵活性。这些组合核函数可以被用于解决各种非线性问题,同时确保我们的SVM或其他基于核的算法能够正确运作。
核函数讨论
常用核函数
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^T \mathbf{x}_j κ(xi,xj)=xiTxj | |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i^T \mathbf{x}_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d \geq 1 d≥1为多项式的次数, d = 1 d = 1 d=1时退化为线性核。 |
| 高斯核(RBF核) | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ 2 2 σ 2 ) \kappa(x_i, x_j) = \exp\left( -\frac{|x_i - x_j|^2}{2\sigma^2} \right) κ(xi,xj)=exp(−2σ2∣xi−xj∣2) | σ > 0 \sigma > 0 σ>0 为高斯核的带宽(width). |
| 指数径向基核(拉普拉斯核) | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ σ ) \kappa(x_i, x_j) = \exp\left( -\frac{|x_i - x_j|}{\sigma} \right) κ(xi,xj)=exp(−σ∣xi−xj∣) | σ > 0 \sigma > 0 σ>0 |
| Sigmoid核 | κ ( x i , x j ) = tanh ( β x i T x j + θ ) \kappa(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\beta \mathbf{x}_i^T \mathbf{x}_j + \theta) κ(xi,xj)=tanh(βxiTxj+θ) | tanh为双曲正切函数, β > 0 , θ < 0 \beta > 0, \theta < 0 β>0,θ<0 |
使用核函数经验
- 文本数据——线性核
- 情况不明——高斯核