MacOS对文件夹加密的方法

news2024/11/19 15:30:29

背景

MacOS没有那种类似于windows那种对文件夹加解密的软件，MacOS自带有一种加解密，但是其实使用体验上跟windows那种很不一样。

win上的加解密都很快，就好像仅仅对文件夹进行加解密（我估计是安全性较低的，因为加密过程瞬间完成）

MacOS所谓的对文件夹的加解密，类似于压缩软件，比如winRAR那种，打成一个压缩包并且设置了密码，MacOS上对某个文件夹加密后就成为一个*.dmg的文件，加密过程设置密码，解密过程输入密码，输入密码后就以挂载盘的形式挂载Finder上

使用MacOS加解密的一些细节

1、加解密过程

打开磁盘管理器（英文叫 Disk Utility），选择 File -> New Image -> Image from Folder

在这里插入图片描述

浏览到某个想要加密的文件夹，默认的Encryption是none，即不加密，要选择128或256的加密，建议使用128的，加密速度较快，Image Format默认是compressed，这个格式加密后后续不能往里面加减文件，建议选择read/write，这样以后可以往里面增减文件。

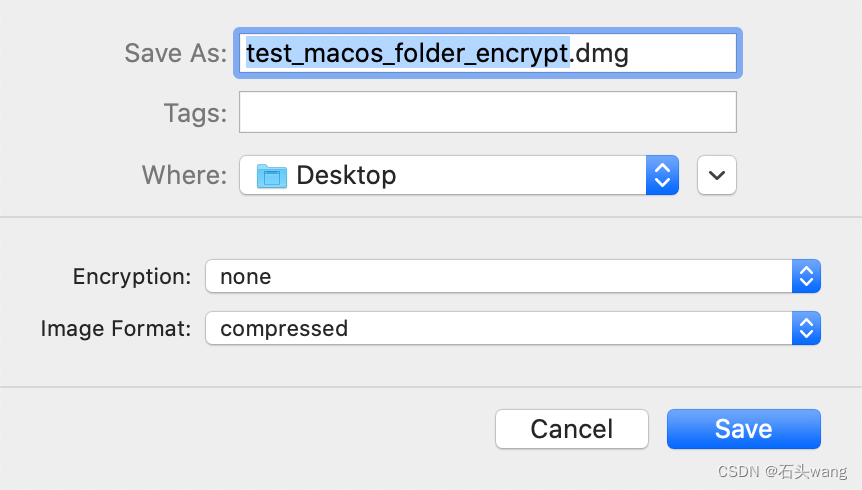
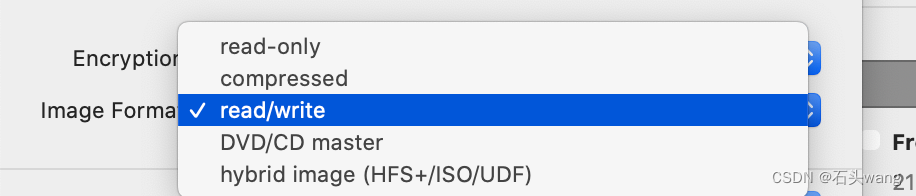
在这里插入图片描述

其他细节：

a文件夹被加密后就是a.dmg文件，双击a.dmg打开时要求输入密码，密码就是加密时输入的，正确之后a.dmg跟那些安装程序的压缩包*.dmg一样，是挂载到Finder中的。如果要退出加密，直接"推出"(Eject)即可
注意输入密码解密a.dmg的时候，不要勾选保存密码，否则加密还有什么意义？？（外国人的脑袋真的奇葩，奇葩脑回路）
被加密的a.dmg是可以被删除的，跟普通的文件一样（外国人的脑回路真奇葩，至少你特殊二次甚至三次确认，甚至输入密码才能删除吧）
加密的a.dmg居然比原来的文件夹占用的空间还多
加密的速度决定于要加密的文件夹的大小，如果文件夹很大，加密也将耗时耗CPU
虽然加密的时候耗时，但是解密的时候很快(秒速)，不管被加密时的内容很大也可以很快解密
如果选择 read/write，则可以往里面继续添加文件，或删除里面的文件
删除a.dmg里的文件，比如里头的 f 文件，则f也会移动到Trash中，但是如果 a.dmg 推出后(退出加密)会隐藏掉 f，而且清空回收站并不会清空掉 f（只有在 a.dmg 解密的状态下清空回收站才会清理掉 f）
如果忘记密码，似乎没有办法，所以一定一定要记住密码！
如果你要加密50G的东西，你得还有50G的空间，因为创建a.dmg之后也要占用50+G，你有这个空间，才能顺利创建a.dmg（之后就可以删除被加密的文件了）（外国人的脑回路。。。你能在原来的基础上加密吗？还得在容量紧张的情况下这么做。。）
他这种加密就是实打实的加密，就是闪存盘被拆了也难解密（不同于那种加密速度很快的软件(其实可能并没有加密，只是文件改了个扩展名，好一些的就是将文件的前几个字节改一下)，外国人虽然做应用不太行，但是安全性实打实还是比较厉害的）
加密后的a.dmg是可以随意移动位置的（不用担心移动路径后加密失效）