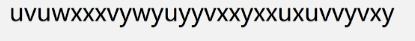文章目录

前言
5.7.1 哈夫曼树的基本概念
- 哈夫曼树的特点
5.7.2 哈夫曼树的构造算法
- 哈夫曼树的构造过程
- 哈夫曼算法的实现
- - 算法思路
  - 算法实现
5.7.3 哈夫曼编码
- 哈夫曼编码思想
- - 前缀编码
  - 哈夫曼编码
  - 哈夫曼编码的性质
- 哈夫曼编码的算法实现
- 文件的编码和解码

前言

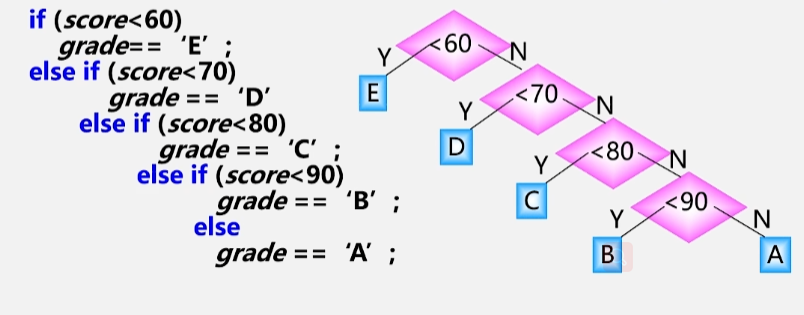
编程：将学生的百分之成绩转换成五分制（ABCDE）成绩

如：<60：E，60-69：D，70-79：C，80-89：B，90-100：A

可以将这样一个判断的过程画成一棵二叉树，每次判断的结果都有两个分支。这样一棵树就称为判断树。

判断树：*用于描述分类过程的二叉树。

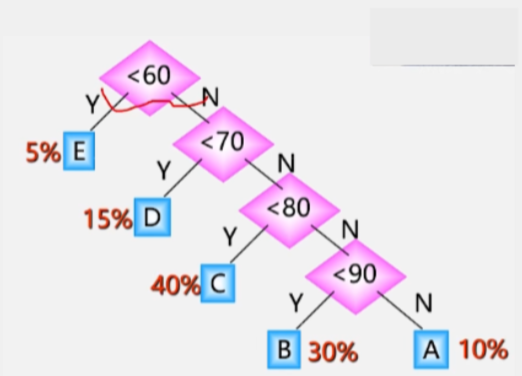
假设出现这样一种情况

小于 60 分的同学只有 5%，大于 90 的同学只有 10%。
最多的同学是在 60 -90 之间。

如果每次的输入量很大，则应该考虑程序的操作时间。
若学生的成绩数据有 10000 个：

60-70 分的同学就需要比较两次（先判断是否小于60再判断是否小于70）
同理：70-80 的同学需要比较三次，80-90 要4次，90分以上也是4次。
每个分数线的人数百分比数据总量比较次数，这样的操作量就很大了。
- 如：处于 60-70 的同学的成绩数据操作数为 15% * 10000 * 2，要比较这么多次，其余同理。

怎样才能让操作次数变少？

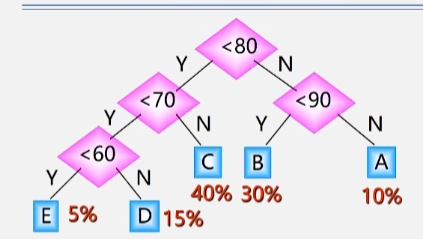
如果将判断树设计成这样

先判断成绩是否小于 80 ，小于走左子树，大于则走右子树（类似于二分法）。
- 小于 60 分和 60-70 分的数据需要比较三次。
- 70-80 、 80-90 以及大于 90 的这三种情况都只需要比较两次。
将值判断三次的数据占比相加，将只判断两次的数据占比相加
这种情况总共需要比较：10000（3 * 20% +2 * 80%） = 22000次

问题：怎样才能找到一种效率最高的判断树呢？这时候就轮到哈夫曼树（最优二叉树）来干活了。

5.7.1 哈夫曼树的基本概念

哈夫曼树又称为最优树，作用是找到一种效率最高的判断树。

路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
结点的路径长度：两个结点之间路径上的分支数。
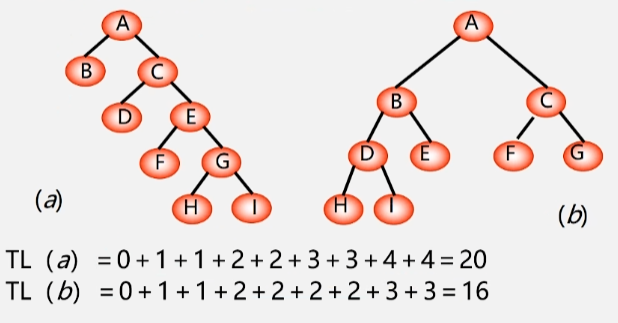
- 如图 a ：从 A-D 的路径长度就是是2。从 A 到 B C D E F G F I 的路径长度分别为 1 1 2 2 3 3 4 4
- 如图 b：从 A 到 B C D E F G H I 的路径长度分别为 1 1 2 2 2 2 3 3。

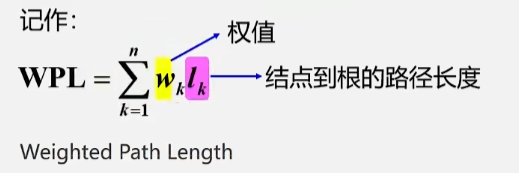
树的路径长度：从树根到每一个结点的路径长度之和称为树的路径长度。记作：TL（根节点到它自身的结点路径长度为0）
- 结点数目相同的二叉树中，完全二叉树是路径长度最短的二叉树，但是路径长度最短的不一定是完全二叉树。

权（weight）：将树中结点赋个一个有着某种含义的数值，则称这个数值为该结点的权。
- 如前言中的那两棵树的每个结点的百分数，权不固定，取什么都可以。
结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积
- 如前言中的树中的小于60分的人数占比 X 到该分支的判断次数（ 5% X 3，）5%即使权，3就是路径长度。
树的带权路径长度：树中所有叶子结点的带权路径之和。

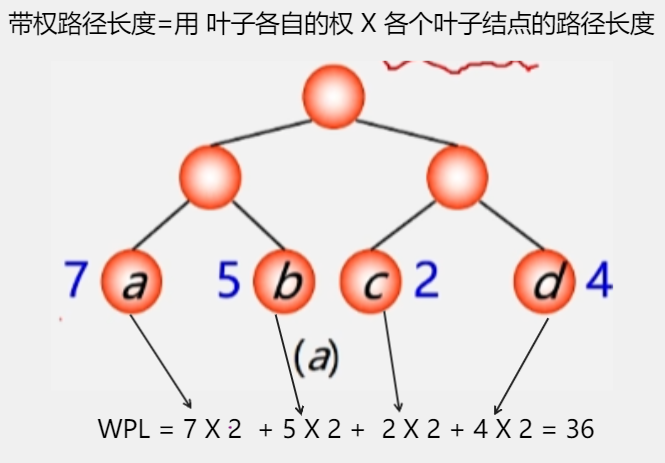
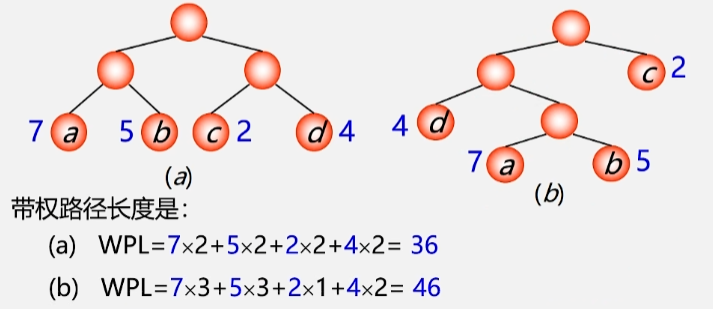
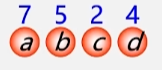
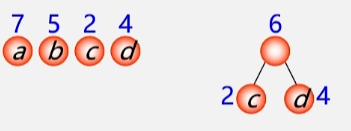
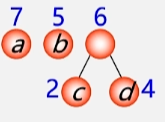
例：有 4 个结点 a b c d，权值分别为 7 5 2 4，构造以此 4 个结点为叶子结点的二叉树。

哈夫曼树：

最优树：树的带权路径长度（WPL）最短的树。
- 带权路径长度最短是在树的度相同的树中比较而得到的结果，因此有最优二叉树，最优三叉树之称等等。
最优二叉树：树的带权路径长度（WPL）最短的二叉树

哈夫曼树的特点

权值越大的结点，离根节点越近，权值越小的结点，离根节点越远，能使总路径越短。

满二叉树不一定是哈夫曼树。
具有相同带权节点的哈夫曼树不唯一，如上图的 3树和4树，都是哈夫曼树但并不是同一棵树。

5.7.2 哈夫曼树的构造算法

在前面知道了哈夫曼树中权越大的叶子离根越近，那么现在我们就要用这样的一个权值来构造哈夫曼树。

贪心算法

构造哈夫曼树时首选选择权值小的叶子结点。
这样就可以将权值大的叶子放到后面构造，大的留在最后就可以离根近一些。

哈夫曼树的构造过程

根据 n 个给定的权值 {W₁，W₂，W₃…，Wn} 构成 n 棵二叉树的森林 F = {T₁，T₂，T₃…，Tn}，其中 Ti 只有一个带权威 Wi 的根节点。
- 构造的森林全是根。这个森林中，给了几个权值就有几棵树。
在森林 F 中选取两棵根节点的权值最小的树作为左右子树，构造一棵新的二叉树，且设置新的二叉树的根节点的权值为其左右子树上根结点的权值之和。
- 选用两小造新树
在森林 F 中删除这两棵树，同时将新得到的二叉树加入森林中。
- 删除两小添新人
重复上面的步骤2 和步骤3，直到森林中只有一棵树为止，这棵树即为哈夫曼树。
- 重复 2、3 剩单根

举个栗子

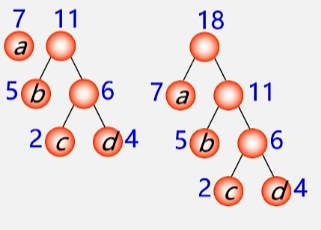
有 4 个结点分别是 a b c d 权值分别为 7 5 2 4，试构造哈夫曼树。

构造的森林全是根。

选用两小造新树。

删除两小添新人。

重复 2、3 剩单根

因为构造哈夫曼树的时候是，选用两小造新树。

所以：哈夫曼树的结点的度为 0 或 2，没有度为 1 的结点。
包含 n 个叶子结点的哈夫曼树中共有 2n -1 个结点。

总结

在哈夫曼算法中，初始时有 n 棵二叉树，要经过 n-1 次合并最终成为哈夫曼树。
经过 n-1 次合并产生 n-1个新结点，且这 n-1 个新结点都是具有两个孩子的分支结点
可见：哈夫曼树中共有 n+n-1 = 2n-1 个结点，且其所有的分支结点的度均不为1.

哈夫曼算法的实现

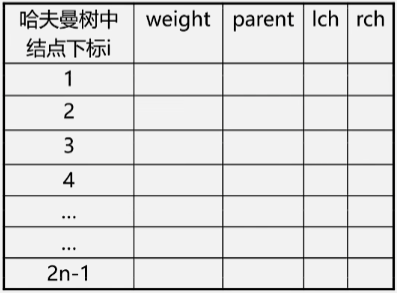
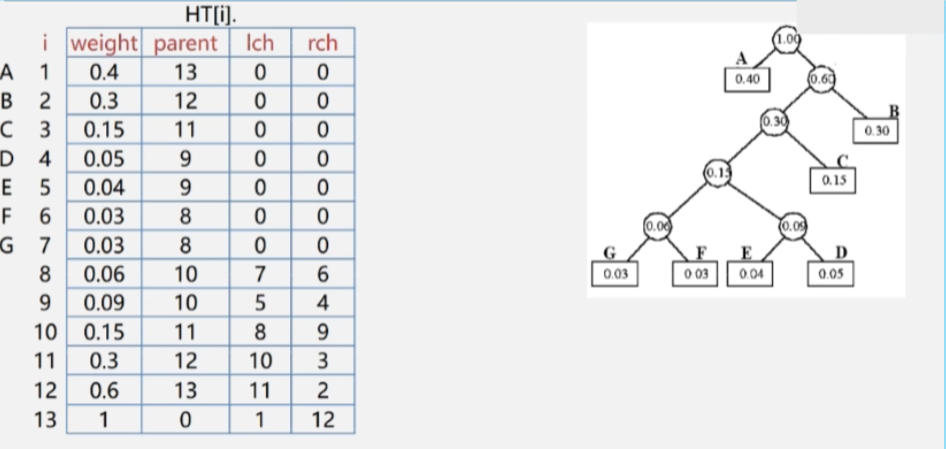
采用顺序存储结构—— 一维结构数组
结点类型定义

typedef struct
{
		int weight;//结点的权重
		int parent;//结点的双亲
		int lchild,rchild;//结点的左、右孩子下标

	}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树

哈夫曼树中共有 2n-1 个结点，不使用 0 下标，数组大小为 2n。
- 例如：第一个结点的权值为 5，即可表示为 H[i].weight = 5

算法思路

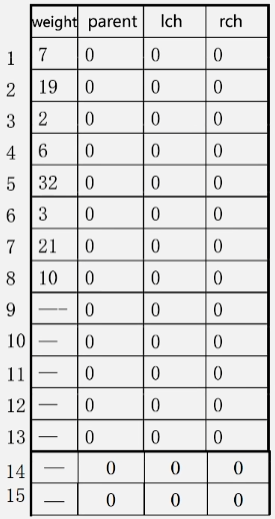
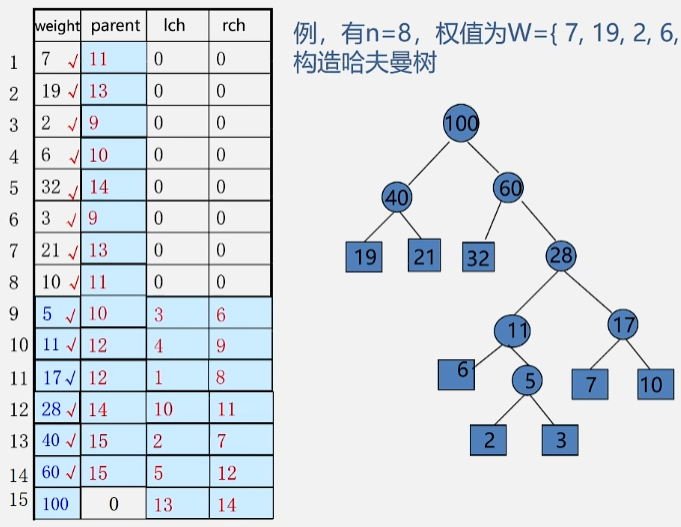
有 8 个权值为 W ={7,19,2,6,32,3,21,10} 的叶子结点，构造哈夫曼树。
这棵哈夫曼树则有 2n-1=2*8-1=15 个结点。
那么现在就应该构造有 2n = 2*8= 16 个元素的数组。

算法实现

初始化 HT [1…2n-1]：lchild = rchild = parent = 0;
输出初始 n 个叶子结点：置为 HT[1…n] 的weight值；
进行以下 n-1 此合并，依次产生 n-1 个结点 HT[i]，i = n+1…2n-1：
- 在HT[1…i-1] 中选两个未被选过（从parent == 0 的结点中选）的 weight 最小的两个结点 HT[s1] 和 HT[s2]，s1、s2为两个最小结点下标。
- 修改 HT[s1] 和 HT[s2] 的 parent 值：HT[s1].parent = i；HT[s2].parent = i；
- 修改新产生的 HT[i]：
  - HT[i].weight = HT[s1].weight + HT[s2].weight;
  - HT[i],lchild = s1;HT[i].rchild = s2

//哈夫曼树的存储表示
typedef struct
{
		int weight;//结点的权重
		int parent;//结点的双亲
		int lchild,rchild;//结点的左、右孩子下标

}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树

//构造哈夫曼树HT
void CreateHuffmanTree(HuffmanTree &HT,int n)
{
		if(n<=1)
		{
				return 0;
		}
		
		int i;
		int m = 2*n-1
		
		HT = new HTNode[m+1];//0号下标未使用，所以需要动态分配m+1(2n)个单元，HT[m]表示根节点
		
		for(i = 1;i<=m;i++)//将1-m个元素的双亲、左右孩子的下标都初始化为0
		{
				H[i].parent = 0;
				H[i].lch = 0;
				H[i].rch = 0;
		}
		for(i = 1;i <= n;i++)//输入前n的元素中，叶子结点的权值
		{
				cin >> HT[i].weight;
		}
//-------------------------初始化结束，下面开始创建哈夫曼树-------------------------//
		//通过n-1次的选择、删除、合并来创建哈夫曼树
		for(i=n+1;i<=m;i++)//从9开始到15结束
		{
				select(HT,i-1,s1,s2);//select函数是自己写的
				//在HT[k](1<=k<=i-1)中选择两个其双亲域为0，且权值最小的结点，并返回他们在 HT 中的序号 s1 和 s2 
				
				HT[s1].parent = i;
				HT[s2].parent = i;
				//得到新结点i,从森林中删除 s1,s2,将 s1 和 s2 的双亲域由0改1

				HT[i].lchild = s1;
				HT[i].rchild = s2;
				//将s1，s2分别作为 i 的左右孩子

				HT[i].weight = HT[si].weight + HT[s2].weight;
				//i的权值为左右孩子的权值之和
		}
}

5.7.3 哈夫曼编码

哈夫曼编码思想

前缀编码

如果在一个编码方案中，任一字符的编码都不是另一个字符的编码的前缀，这种编码称作前缀编码。

举个栗子

在远程通讯汇总，要将待传字符转换成由二进制的字符换
设要传送的字符为：ABACCDA，现要将这7个字符转换成由01构成的二进制编码。每个字符都用1个两位的二进制编码表示。
- 若编码为：A - 00，B - 01，C - 10，D - 11
- 那么这一串字符就可以转换成 A B A C C D A ——> 00 01 00 10 10 11 00
这种编码的方式就称为定长编码，定长编码的缺点就是比较浪费空间，这串字符只有4个不同的字母，但是每个字母都需要占用两个 bit 位。
若将斑马设计为长度不等的二进制编码，即让待传字符串中出现次数较多的字符采用尽可能短的编码，则转换的二进制字符串便可能减少。

前缀编码的缺点

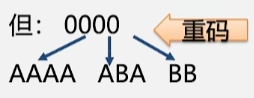
这个时候我们又发现了一个问题，这串二进制码中有重码，ABA转换成的0使得前面出现了4个0。这样的编码就出现前缀了

在将二进制翻译成字符的时候就会出现多种情况了。

所以在设计长度不等的编码时，一定不能有重码。

关键：要设计长度不等的编码时，则必须使任一字符的编码都不是另一个字符的编码的前缀，这种编码称作前缀编码。

哈夫曼编码

对一棵具有 n 个叶子的哈夫曼树，若对树中的每个左分支赋予 0 ，右分支赋予 1 ，则从根到每个叶子的路径上，各个分支的赋值分别构成一个二进制串，该二进制串就称为哈夫曼编码。

问题：什么样的前缀码能使的电文总长最短？

统计字符集中每个字符在电文中出现的平均概率（概率越大，要求编码越短）。
利用哈夫曼树的特点：权越大的叶子离根越近：将每个字符的概率作为权值，构造哈夫曼树。则概率越大的结点，路径越短。
在哈夫曼树的每个分支表上 0 或 1：
- 结点的左分支标 0，右分支标 1。
- 把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的字符的编码。

举个栗子

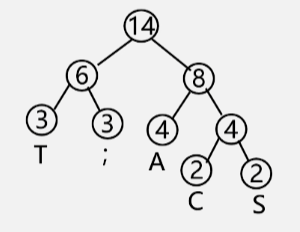
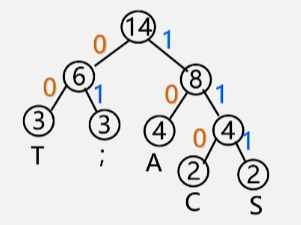
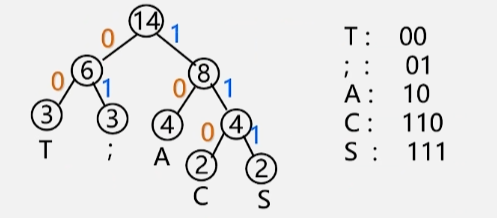
【例】要传输的字符集 D = {C，A，S，T，; }（注意这个分号也是，并没有多打），每个字符出现的频率 W = {2，4，2，3，3}

以每个字符出现的频率作为权值来构造哈夫曼树：构造的森林全是根，选用两小造新树，删除两小添新人，重复 2 、3 剩单根。

将这棵哈夫曼树中所有的左分支标 0，右分支标 1。

从根节点出发，到每一个叶子结点，将路径上经过的 01 标号连起来。
- 如：从根到 T 字符，经过了 00 分支，所以 T 的编码就是 00。

哈夫曼编码的两个问题

为什么哈夫曼编码能够保证是前缀编码？

因为没有一片叶子是另一片叶子的祖先，所以每个叶子结点的编码就不可能是其他叶子结点编码的前缀。

为什么哈夫曼编码能够保证字符编码总长最短？

因为哈夫曼树就是树的带权路径长度最短的树，所以整个字符编码的总长最短。

哈夫曼编码的性质

性质1：哈夫曼编码是前缀编码（任一字符的编码都不是另一字符的编码的前缀）。
性质2：哈夫曼编码是最优前缀码。

小试牛刀

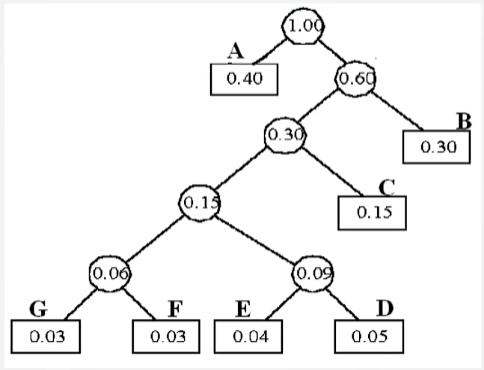
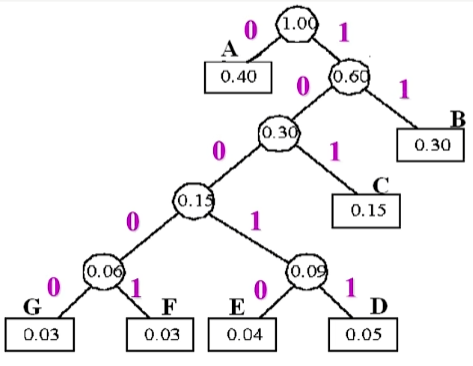
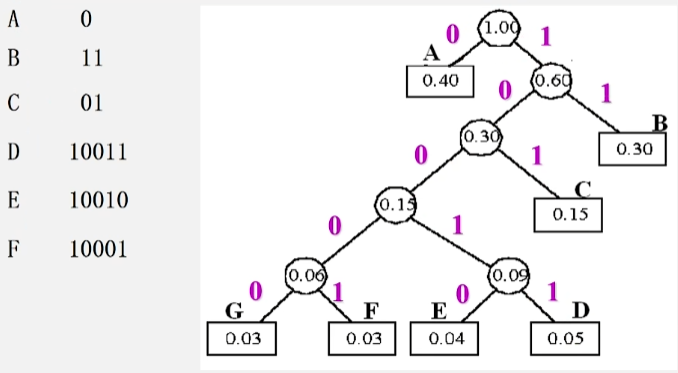
假设组成电文的字符集 D 及其概率分布 W 为：

D = {A，B，C，D，E，F，G}
W = {0.40，0.30，0.15，0.05，0.04，0.03，0.03}

设计哈夫曼编码

先构造一棵哈夫曼树。

给所有的左分支标记为 0，给所有的右分支标记为 1。

从根节点到每个叶子结点所经过的标号，就是对应字符的编码。

哈夫曼编码的算法实现

由于从根节点到叶子结点构造哈夫曼编码用算法来实现比较困难，所以在构造哈夫曼树后，求哈夫曼编码的主要思想是：
- 依次以叶子结点为起点，向上回溯至根节点为止。回溯时如果走左分支则生成代码 0 ，走右分支则生成代码 1。

假设要找到 G 结点的哈夫曼编码

查到 G 在数组当中的位置是 7，取出 7 号结点的 parent 域的值，发现是 8 意思就是 8 号结点是它的双亲。
在 8 号结点的左孩子域找到了 7，说明 7号结点是 8号的左孩子，是左孩子那么就标注为 0 。
依次类推直到找到 parent 域为0的结点，就说明G沿着路线走到根节点了。

但是哈弗曼编码是从根到叶子走过的编码，所以要将上述步骤得到的编码翻过来，得到哈夫曼编码。
有 n 个字符上面的步骤就要重复 n 次。

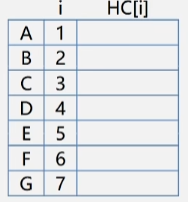
每一个字符都是由若干个 01 组成的哈夫曼编码，所以n 个字符就需要准备 n 个字符串，

由于每个哈夫曼编码是变长编码，因此使用一个指针数组来存放每个字符编码串的首地址。

用一个字符数组来装下 01 编码构成的字符串

有 n 个字符的话，由这 n 个字符所构成的哈夫曼树最高有 n - 1层，因为哈夫曼树一开始坑定是选用两小造新树。
现在有 7 个字符，所以由 01 构成的字符串最长也就是 n -1 = 6，然后数组要多一个元素的位置来存放字符串最后的 \0。

算法步骤

分配存储 n 个字符编码的编码表空间 HC，长度为 n + 1；分配临时存储每个字符编码的动态数组空间 cd，cd[n-1]置为 ‘\0’。
逐个求解 n 个子字符的编码，循环 n 次，执行以下操作：
- 设置变量 start 用于几轮编码在 ca 中存放的位置，start 初始时指向最后一个元素的位置，即编码结束符 ‘\0’ 的位置。
- 设置变量 c 用于记录从叶子结点向上回溯至根节点所讲过的结点下标， c 初始时为当前待编码字符的下标 i，f 用于记录 i 的双亲结点的下标；
- 从叶子结点向上回溯至根结点，求得字符 i 的编码，当 f 没有到达根节点时，循环执行以下操作：
  - 回溯一次 start 向前指一个位置，即 --start；
  - 若结点 c 是 f 的左孩子，则生成代码 0，反之生成代码 1，生成的代码 0 或 1保存在 ca[start] 中。
  - 继续向上回溯，改变 c 和 f 的值。
- 根据数组 cd 的字符串长度为第 i 个字符编码分配空间 HC[i]，然后将数组 cd 中的编码复制到 HC[i] 中。
释放临时空间 cd 。

算法描述

//从叶子到根逆向求每个字符的哈夫曼编码，并且存储在编码表 HC 中
void CreatHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n)
{
		HC - new char*[n+1];//分配存储 n 个字符编码的编码表空间
		cd = new char[n];//分配临时存放每个字符编码的动态数组空间
		cd[n-1] = '\0';//编码结束符（字符串结束符）

		for(i=1;i<=n;i++)//逐个字符求哈夫曼编码
		{
				start = n-1;//start 一开始指向数组最后的位置，即存放 '\0' 的位置
				c = i;
				f = HT[i].parent;//让 f 指向 c 的双亲结点

				while(f != 0)//f没有走到根节点时执行循环
				{
						start--;//回溯一次使 start 向前指一个位置
						if(c == HT[f].lchild)
						{
								cd[start] = '0';//如果结点 c 是结点 f 的左孩子，则生成代码 0
						}
						else
						{
								cd[start] = '1';//如果结点 c 是结点 f 的右孩子，则生成代码 1
						}
						c = f;f = HT[f].parent;//继续向上回溯
				}//求出第 i 个字符的编码

				HC[i] = new char[n-start];//为第 i 个字符的编码分配空间
				strcpy(HC[i],&cd[start]);//将求得的字符编码从空间 cd 当中复制到 HC 的当前行中
		}
		delete cd;//释放临时空间

}//CreatHuffmanCode