继续关于ceres官方doc里教程的学习,对于powell's function的学习。
一、powell's function
鲍威尔法,严格来说是鲍威尔共轭方向法,是迈克尔J.D.鲍威尔提出的一种求解函数局部最小值的算法。该函数不能是可微分的,并且不会导出衍生函数。
该函数必须是固定数量的实值输入的实值函数。通过传入一组初始搜索向量,通常会传入N个搜索向量(譬如{s1,,,,,sn})这是与每个轴对齐的法线。
鲍威尔法是在无约束优化共扼方向,从某个初始点出发,求目标函数在这些方向上的极小值点,然后以该点为新的出发点,取复这一过程直到获得满意解,其优点是不必计算目标函数的 梯度就可以在有限步内找到极值点。
以上内容引用自百科,直接看官方的例子:
它的意思是说, F(x)是上面四个残差值的方程,现在要寻找合适的x使最小。
下面使用ceres进行求解。
二、定义残差方程
按照前面学习的步骤,进行定义:
struct f1{
template<typename T>
bool operator()(const T* const x1, const T* const x2, T* residual) const {
residual[0] = x1[0] + 10.0 * x2[0];
return true;
}
};
struct f2{
template<typename T>
bool operator()(const T* const x3, const T* const x4, T* residual) const {
residual[0] = sqrt(5) * (x3[0] - x4[0]);
return true;
}
};
struct f3{
template<typename T>
bool operator()(const T* const x2, const T* const x3, T* residual) const {
residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
return true;
}
};
struct f4{
template<typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
residual[0] = sqrt(10) * (x1[0] - x4[0]) * (x1[0] - x4[0]) ;
return true;
}
};这里我调试的时候,犯了几个错误,记录一下:
1. 关于x1的设置,要写成x1[0]的形式。
2. 所有的数要写成double的形式。10 要写成 10.0。
三、构建寻优问题
Problem problem;
problem.AddResidualBlock(new AutoDiffCostFunction<f1, 1, 1, 1>(new f1), NULL, &x1, &x2);
problem.AddResidualBlock(new AutoDiffCostFunction<f2, 1, 1, 1>(new f2), NULL, &x3, &x4);
problem.AddResidualBlock(new AutoDiffCostFunction<f3, 1, 1, 1>(new f3), NULL, &x2, &x3);
problem.AddResidualBlock(new AutoDiffCostFunction<f4, 1, 1, 1>(new f4), NULL, &x1, &x4);也是按照之前的格式来写的,没什么问题。
四、配置并运行求解器
Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
Solver::Summary summary;
Solve(options, &problem, &summary);五、输出结果
cout << summary.BriefReport() << "\n";
cout << "x1 : " << x1 << "\n";
cout << "x2 : " << x2 << "\n";
cout << "x3 : " << x3 << "\n";
cout << "x4 : " << x4 << "\n";最后算出来到结果是:
基本上和0,差不多。符合官网的参考答案。
六、换成其它的格式
#include <ceres/ceres.h>
#include <iostream>
using namespace std;
using namespace ceres;
struct f{
template<typename T>
bool operator()(const T* const x, T* residual) const {
residual[0] = x[0] + 10.0 * x[1];
residual[1] = sqrt(5) * (x[2] - x[3]);
residual[2] = (x[1] - 2.0 * x[2]) * (x[1] - 2.0 * x[2]);
residual[3] = sqrt(10) * (x[0] - x[3]) * (x[0] - x[3]) ;
return true;
}
};
int main(int argc, char** argv)
{
double x[4] = {1,2,3,4};
Problem problem;
problem.AddResidualBlock(new AutoDiffCostFunction<f, 4, 4>(new f), NULL, x);
Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
Solver::Summary summary;
Solve(options, &problem, &summary);
cout << summary.BriefReport() << "\n";
cout << "x1 : " << x[0] << "\n";
cout << "x2 : " << x[1] << "\n";
cout << "x3 : " << x[2] << "\n";
cout << "x4 : " << x[3] << "\n";
return 0;
}
按造自己的想法,优化了下。主要是使用了x数组代替了4个单独的变量,并重新设置residual的纬度。需要注意的是,problem.AddResidualBlock()函数中最后一个参数,原来是单个数就需要取地址符号,设置成数组就直接写数组名就好了。
最后算出结果:
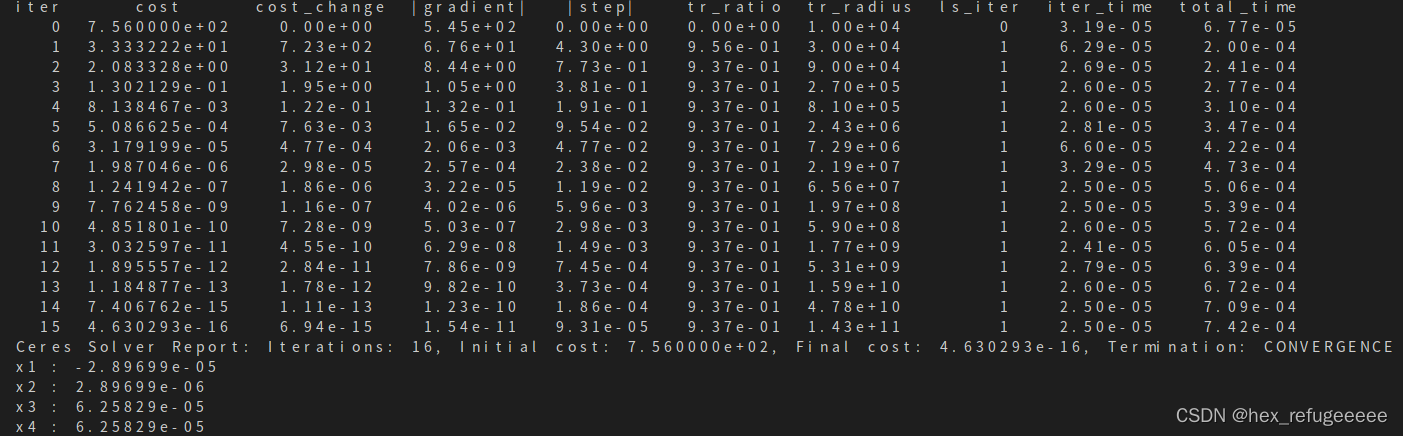
两次结果基本一致。
准备把官方doc里面的example部分全部刷一遍。