在数据分析的世界里,我们经常面临着处理高维数据的挑战。随着维度的增加,数据处理、可视化以及解释的难度也随之增加,这就是所谓的“维度的诅咒”。主成分分析(PCA)是一种强大的统计工具,用于减少数据的维度,同时尽量保留最重要的信息。这篇文章将带你深入了解PCA的原理、过程和应用。
1. PCA的基本概念
主成分分析(PCA)是一种多元统计技术,主要用于数据的降维处理。通过PCA,可以将多个变量转化为少数几个称为“主成分”的新变量,这些主成分能够捕捉数据中的主要变异性。
2. 工作原理
PCA的工作原理基于一个数学概念:线性代数中的特征值和特征向量。具体来说,PCA通过寻找数据的协方差矩阵(或相关矩阵)的特征向量来工作,这些特征向量定义了数据中变异最大的方向。这些方向(或称为主轴)是正交的,确保了新变量之间的独立性。
3. PCA的步骤
实施PCA通常涉及以下几个步骤:
- 标准化数据:由于PCA受数据尺度的影响很大,通常需要首先对数据进行标准化处理,使得每个特征的平均值为0,标准差为1。
- 计算协方差矩阵:分析特征之间的协方差,或者在数据标准化后计算相关矩阵。
- 特征值分解:计算协方差矩阵的特征值和对应的特征向量。
- 选择主成分:根据特征值的大小(表示每个主成分的信息量)选择顶部的几个特征向量,这些向量代表了数据中的主要变异方向。
- 构造新特征:使用选定的特征向量将原始数据转换到新的特征空间,这些新的特征就是我们的主成分。
4. PCA的应用
PCA的应用广泛,涉及各个领域:
- 数据可视化:通过将高维数据降至二维或三维,PCA可以帮助我们可视化数据结构,便于观察样本之间的相似性和差异性。
- 去噪:PCA可以通过忽略那些贡献较小的成分来滤除噪声,强化数据中最重要的信号。
- 特征抽取和数据压缩:在机器学习模型中,使用PCA可以减少特征的数量,提高算法的效率和性能。
5. PCA的局限
尽管PCA非常有用,但它也有局限:
- 线性假设:PCA假设主成分之间是线性关系,对于非线性关系的数据结构可能不适用。
- 方差最大化可能不总是最优:有时数据中最重要的特征并不一定是方差最大的方向,特别是当这些方向受噪声影响较大时。
- 敏感性:对异常值非常敏感,异常值可能会严重影响PCA的结果。
6. 优化和替代方法
鉴于PCA的一些局限性,研究者们开发了多种方法来优化或替代传统的PCA:
- 稀疏PCA:在传统PCA的基础上增加了稀疏性约束,可以产生更易解释的主成分,由于主成分中只包含少数几个变量,因此更容易理解。
- 核PCA:通过将数据映射到高维空间,核PCA能够处理非线性数据结构。它使用核技巧来计算在高维特征空间中的主成分,从而揭示数据中的非线性关系。
- 增量PCA:适用于数据量非常大的情况,可以逐步计算主成分,无需一次性将所有数据加载到内存中。
7. 实际示例:使用Python进行PCA
让我们看一个使用Python的sklearn库来执行PCA的简单示例,该示例使用经典的鸢尾花(Iris)数据集:
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 加载数据
data = load_iris()
X = data.data
y = data.target
# 实例化PCA对象,设置降维后的维数为2
pca = PCA(n_components=2)
# 对数据进行PCA处理
X_pca = pca.fit_transform(X)
# 可视化结果
plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.colorbar(scatter)
plt.title('PCA of Iris Dataset')
plt.show()
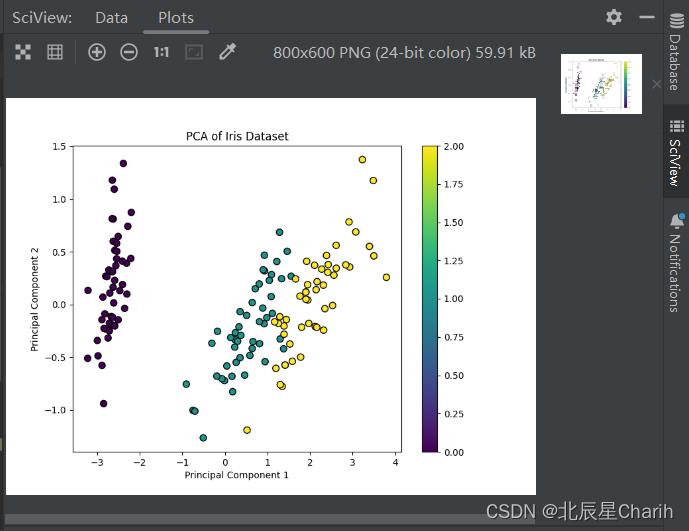
在这个示例中,我们使用PCA将鸢尾花数据集的四个特征降至两个维度,这样就可以在二维平面上可视化不同类别的数据点。结果显示,不同种类的鸢尾花在主成分分析后可以被相对清晰地区分开。
8. 结论
主成分分析(PCA)是多元统计分析中一个非常有用的工具,它不仅帮助我们简化数据,还揭示了数据中的主要趋势和模式。虽然PCA有其局限性,但通过适当的方法选择和参数调整,它仍然是一个在各种应用领域中不可或缺的分析方法。无论是在科学研究、金融分析还是在工业工程中,PCA都展示了其强大的数据处理能力。
![[华为OD]给定一个 N*M 矩阵,请先找出 M 个该矩阵中每列元素的最大值 100](https://img-blog.csdnimg.cn/direct/40139308daa9475a87a987e5e003bd6c.png)