一、函数介绍

• 在 Python 中，函数是一个组织好的、可重用的代码块，用来执行一个单一的、相关的动作。函数提供了代码的模块化和代码复用的能力。它可以接受输入参数，并可以返回一个结果。函数在 Python 编程中是基本的构建块之一。

二、函数的定义

函数的定义：

• 先定义函数
• 后调用函数
• 参数不需要，可以省略
• 返回值不需要，可以省略

def 函数名(传入参数):
    函数体
    return 返回值

示例：

# 定义一个函数，输出相关信息
def say_hello():
    print("hello")

# 调用函数
say_hello()

三、函数的参数

在 Python 中，函数的参数是用来传递信息或数据给函数的变量。通过使用参数，函数可以接收外部的输入值，这些输入值在函数调用时被指定，使函数更具通用性和灵活性。

# 定义两数相加的函数，通过参数接收被计算的2个数字
def add(x, y):
    result = x + y
    print(f"{x}+{y}的计算结果是：{result}")

# 调用函数
add(1,2)

语法解析：

• 函数定义中，x和y，称之为：形式参数（形参），表示函数声明将要使用2个参数
• 参数之间使用逗号分隔
• 函数调用中，1和2，称之为：实际参数（实参），表示函数执行时真正使用的参数值
• 传入的时候，按照顺序传入数据，使用逗号分隔

三、函数的返回值

3.1 什么是函数的返回值

• 函数的返回值是指函数完成执行后传回给调用者的数据。返回值使得函数不只是执行操作，还可以产生结果并将其传递给其他程序的部分。这种机制是函数编程的核心部分，它允许函数与外部代码交互、传递数据和表达式的结果。
• 函数中的 return 语句用于结束函数执行并指定返回值。return 可以跟任何数据类型的对象，包括数字、字符串、列表、字典、元组、布尔值或更复杂的对象。如果函数内部没有 return 语句，或者 return 语句没有跟随任何值，函数默认返回 None。

3.1函数返回值的语法

def 函数名(传入参数):
    函数体
    return 返回值

示例：

# 定义一个函数，完成两数相加功能
def add(a, b):
    return a + b

r = add(1, 2)
print(r)

3.2函数返回值之None类型

• 在 Python 中，如果一个函数没有显式地使用 return 语句返回数据，或者 return 语句后没有跟任何值，那么这个函数依然有返回值，但这个返回值默认是 None。
• None 是 Python 的一个特殊数据类型，用来表示空值或无值的状态。它通常用于标示某些东西不存在或未定义。

示例：

def print_hello():
    print("Hello, world!")

result = print_hello()
print(result)  # 输出 None

四、函数的说明文档

• 函数是纯代码语言，想要理解其含义，就需要一行行去阅读理解代码，效率比较低
• 我们可以给函数添加说明文档，辅助理解函数的作用。

语法：

def func(x, y):
    """
    :param x: 形参x的说明
    :param y: 形参y的说明
    :return: 返回值的说明
    """
    函数体
    return 返回值

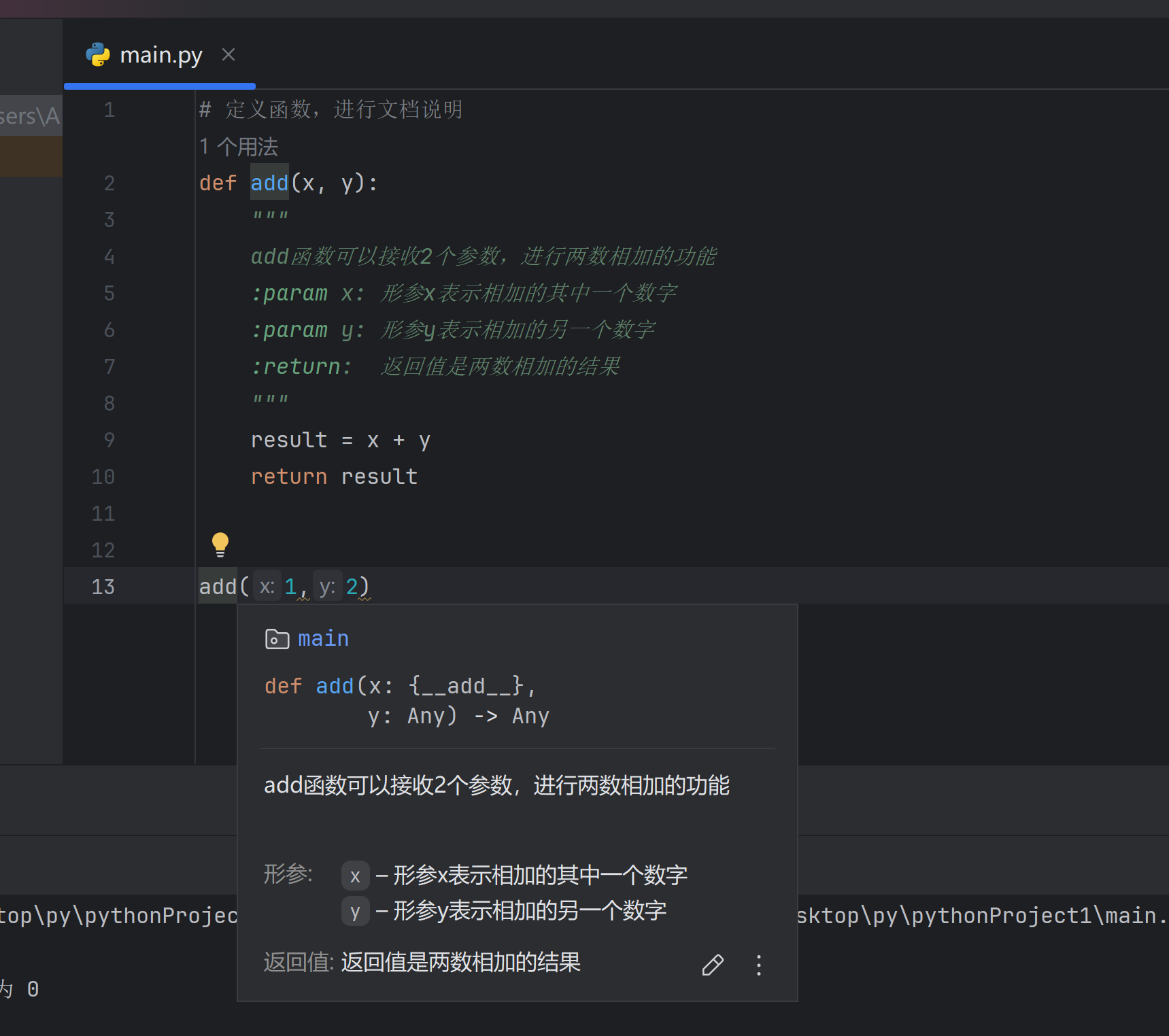
# 定义函数，进行文档说明
def add(x, y):
    """
    add函数可以接收2个参数，进行两数相加的功能
    :param x: 形参x表示相加的其中一个数字
    :param y: 形参y表示相加的另一个数字
    :return:  返回值是两数相加的结果
    """
    result = x + y
    return result

• 在pycharm编写代码时，可以通过鼠标悬停，查看调用函数的说明文档

五、变量的作用域

• 变量作用域指的是变量的作用范围（变量在哪里可用，在哪里不可用）
• 主要分为两类：局部变量和全局变量

5.1局部变量

• 所谓局部变量是定义在函数体内部的变量，即只在函数体内部生效

示例：

# 演示局部变量
def test_a():
    num = 100
    print(num)

test_a()
print(num) # 报错：name 'num' is not defined.

示例中变量num是定义在test_a函数内部的变量，在函数外部访问则立即报错

• 局部变量的作用：在函数体内部，临时保存数据，即当函数调用完成后，则销毁局部变量

5.2全局变量

• 所谓全局变量，指的是在函数体内、外都能生效的变量

示例：

# 演示全局变量
num = 200

def test_a():
    print(f"test_a: {num}")

def test_b():
    print(f"test_b: {num}")

test_a()
test_b()
print(num)

5.3 global关键字

思考：test_a()函数需要修改全局变量num的值为500，如何修改程序？

num = 200
def test_a():
    num = 500
    print(f"test_a: {num}")

def test_b():
    print(f"test_b: {num}")

test_a()
test_b()
print(num)

• 当你在 test_a() 函数中设置 num = 500 时，你实际上是在函数的局部作用域内创建了一个新的变量 num，它只在 test_a() 函数内有效。这个变量是局部变量，它与全局作用域中的 num 是两个完全不同的变量，即使它们的名字相同。
• test_b() 函数内部没有定义局部变量 num，所以当你尝试打印 num 时，Python 查找这个变量名会回退到外部作用域，也就是全局变量 num，其值为 200。
• 最后的 print(num) 语句也是在全局作用域中执行，因此它访问的是全局变量 num，值同样为 200。

global关键字

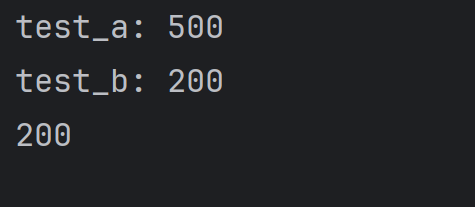
• 如果你希望 test_a() 函数修改全局变量 num，你需要在该函数内部使用 global 关键字来声明 num：
• 在这个修改后的版本中，所有的输出都将是 500，因为 test_a() 现在修改了全局作用域中的 num 变量。

示例

num = 200
def test_a():
    global num
    num = 500
    print(f"test_a: {num}")

def test_b():
    print(f"test_b: {num}")

test_a()
test_b()
print(num)