题目链接

题目描述

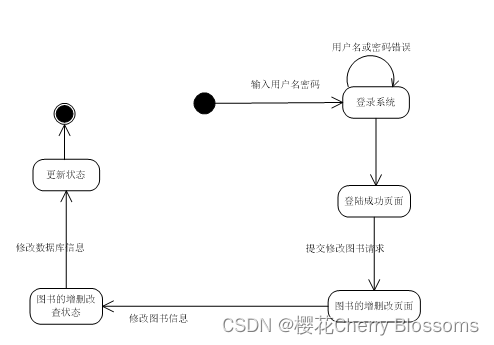
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

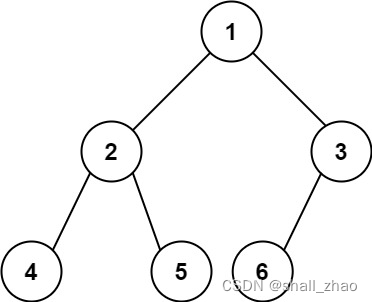
输入：root = [1,2,3,4,5,6]
输出：6
示例 2：

输入：root = []
输出：0
示例 3：

输入：root = [1]
输出：1

解题思路

作为一个菜鸟，当然直接反手一个dfs遍历，提交，over

代码

class Solution {
    public int countNodes(TreeNode root) {
        return dfs(root);
    }

    public int dfs(TreeNode root){
        if(root == null){
            return 0;
        }
        return dfs(root.left) + dfs(root.right) + 1;
    }
}

解题思路二

当然，拿来写题解了，说明这道题目不是如此的简单，如果只是按照dfs或者bfs来解题，代码固然简单，但是时间复杂度是O(N)， 不是最优的。
下面介绍O(logn^2)的时间复杂度解法：

通过二分查找+位运算可以将时间复杂度优化

因为题目中明确的告诉你了这是一颗完全二叉树，所以，要利用好完全二叉树的性质。
完全二叉树第i层最多有$2^i$个节点，最下面的一层节点个数最少为1，最多为$2^i$，所以，只有最下面一层的节点个数是不确定的，但是我们可以根据二叉树的层数确定最少和最大的范围：

• 当最底层包含 1个节点时，完全二叉树的节点个数是：$2^h$

• 当最底层包含$2^h$个节点时，完全二叉树的节点个数是：$2^{h+1}-1$

可以在该范围内通过二分查找的方式得到完全二叉树的节点个数。

具体做法是，根据节点个数范围的上下界，确定当前要判断的节点个数mid，假如mid存在，那说明节点个数比mid多，在后一半搜索，如果，mid不存在，说明节点个数比mid少，在前一半搜索。

那么如何确定mid这个数是否在二叉树中存在呢？技巧是使用位运算。
联想一下我们构造哈夫曼树的办法，我们构造哈夫曼树的时候使用0和1表示向左向右，这里同样可以。

看这个例子

    1            h = 0
   / \
  2   3          h = 1
 / \  /
4  5 6           h = 2

现在这个树中的值都是节点的编号，最底下的一层的编号是$[2^h,2^{h+1}-1]$，现在h=2，也就是4，5，6，7对应二进制分别为 100 101 110 111。不看最左边的1，从第二位开始，0表示向左，1表示向右，正好可以表示这个节点相对于根节点的位置。

那么想访问最后一层的节点就可以从节点的编号的二进制入手。从第二位开始的二进制位表示了最后一层的节点相对于根节点的位置。

那么就需要一个bits = $2^{h-1}$，上面例子中的bits就是2，对应二进制为010。这样就可以从第二位开始判断。（树三层高，需要向左或向右走两次才能到叶子）

比如看5这个节点存不存在，先通过位运算找到编号为5的节点相对于根节点的位置。010 & 101 发现第二位是0，说明从根节点开始，第一步向左走。

之后将bit右移一位，变成001。001 & 101 发现第三位是1，那么第二步向右走。

最后bit为0，说明已经找到编号为5的这个节点相对于根节点的位置，在看这个节点是不是空，不是空说明存在，exist返回真

若编号为5的节点存在，说明总节点数量一定大于等于5。所以二分那里low = mid

再比如看7存不存在，010 & 111 第二位为1，第一部从根节点向右；001 & 111 第三位也为1，第二步继续向右。

然后判断当前节点是不是null，发现是null，exist返回假。

编号为7的节点不存在，说明总节点数量一定小于7。所以high = mid - 1。

解题代码二

class Solution{
    public int countNodes(TreeNode root){
        if(root == null){
            return 0;
        }
        int level = 0;  // 统计多少层
        TreeNode node = root;
        while(node.left != null){
            // 走最左侧的边，能找到最大深度
            level++;
            node = node.left;
        }
        // 确定节点个数的上下界
        int low = 1<<level,high = (1<<(level+1)) - 1;
        while(low < high){
            int mid = (high - low + 1) / 2 + low;
            if(exists(root,level,mid)){
                low = mid;
            }else{
                high = mid- 1;
            }
        }
        return low;
    }

    public boolean exists(TreeNode root, int level, int mid){
        int bits = 1 << (level - 1);   // 需要把bits个位置逐一判断
        TreeNode node = root;
        while(node != null && bits > 0){
            if((mid & bits) == 0){ // 如果这一层是0，向左走
                node = node.left;
            }else{
                node = node.right;  // 是1向右走
            }
            bits >>= 1; // 判断右侧一位是1还是0
        }
        return node != null;  // 如果走到的这个位置是null，说明节点不存在，不是null，说明节点存在
    }
}