ROS学习笔记（14）拉普拉斯变换和PID

news2024/10/7 18:25:49

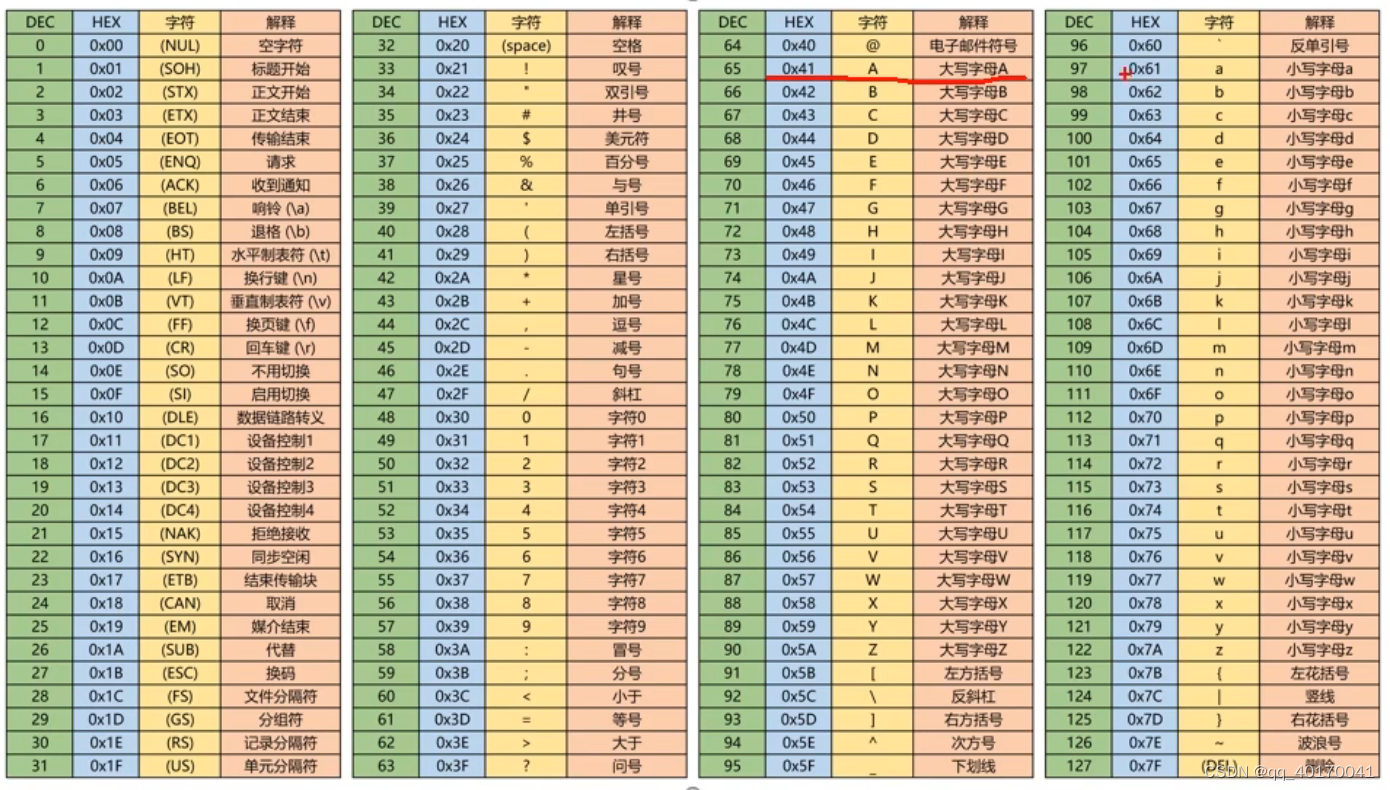
0.前提

近些时间在对睿抗的ROS仿真赛进行小组安排，对小组成员进行了一些安排，也要求他们以本次比赛写下自己的比赛经历博客，他们的培训由我来安排和负责，因此我得加吧油，起码保证我的进度得快过他们，才能安排好本次比赛。好了扯了这么多，进入重点，拉普拉斯变换和PID调节都是能在本科学习期间的自动控制原理当中看到，甚至自控是很多人考研时感到最头疼的科目之一，同时也是为了能更好的调节vesc。

1.拉普拉斯变换

1.拉氏变换概念

公式墙(1)知乎有一个讲的挺好的

在自控中有个弹簧-增块-阻尼器系统，其微分方程如下图：

我简单解释一下这个方程，用牛二可知 $F=fv(t)+ky(t)+ma(t)$ ,根据大学物理知识可知 $v(t)={y(t)}'$ 、 $a(t)={y(t)}''$ ，而y上面的点代表的就是求导。在时域当中求解这个微分方程是相当麻烦的，而拉普拉斯变换给我们提供了一个将时域系统转变为频域系统的方式。

在复变函数(如果没有复变基础请自己去寻找书籍学习一下)中有一个章节来单独对拉普拉斯变换进行了讲解，不过好像在上复变的时候老师都没讲这一章内容，反倒在自控中老师单独花了时间来讲，在上图的拉普拉斯变换的定义中我们可以看到拉普拉斯积分公式：

反演公式就是拉氏反变换

$F(s)=\int_{0}^{+\infty}f(t)e^{-st}dt$

或

$\mathfrak{L}(f)=\int_{0}^{\infty}f(t)e^{-st}dt=F(s)$

在公式中我们将时域 $t$ 转变为频域 $s$ 。而 $f(t)$ 是 $F(t)$ 的拉氏逆变换，记为：

$f(t)=\mathfrak{L}^{-1}[F(s)]$

2.常见的拉氏变换

1.阶跃函数

$f(t)=\begin{cases} 1&t\geq 0\\ 0& t< 0 \end{cases}$

$\mathfrak{L}[1(t)]=\int_{0}^{\infty}1\cdot e^{-st}dt=\frac{-1}{s}[e^{-st}]_{0}^{\infty}=\frac{1}{s}$

2.指数函数

$f(t)=e^{at}$

$\mathfrak{L}[f(t)]=\int_{0}^{\infty}e^{at}\cdot e^{-st}dt=\int_{0}^{\infty}e^{-(s-a)t}dt=\frac{-1}{s-a}[e^{-(s-a)t}]_{0}^{\infty}=\frac{1}{s-a}$

3.正弦函数

$f(t)=\begin{cases} 0 & \ t<0\\ sin\omega t &\ t\geq 0 \end{cases}$

$\mathfrak{L}[f(t)]=\int_{0}^{\infty}sin\omega t\cdot e^{-st}dt=\frac{\omega}{s^{2}+\omega ^{2}}$

其余的常见拉氏变换我用图片放出来，其实记住上面的定义式 $\mathfrak{L}(f)=\int_{0}^{\infty}f(t)e^{-st}dt=F(s)$ 都可以自己计算出来，唯一值得注意的就是复变里面的 $-1=j^{2}$ ：

3.拉氏变换几个重要性质

在拉氏变换中有几个重要的性质，为了方便我同样只放图片：

2.PID

自控当中有介绍到PID（比例-积分-微分控制器），利用系统误差、误差的微分和积分信号构成控制规律，PID控制器采用不太组合可实现PD，PI，PID这3种矫正方式。

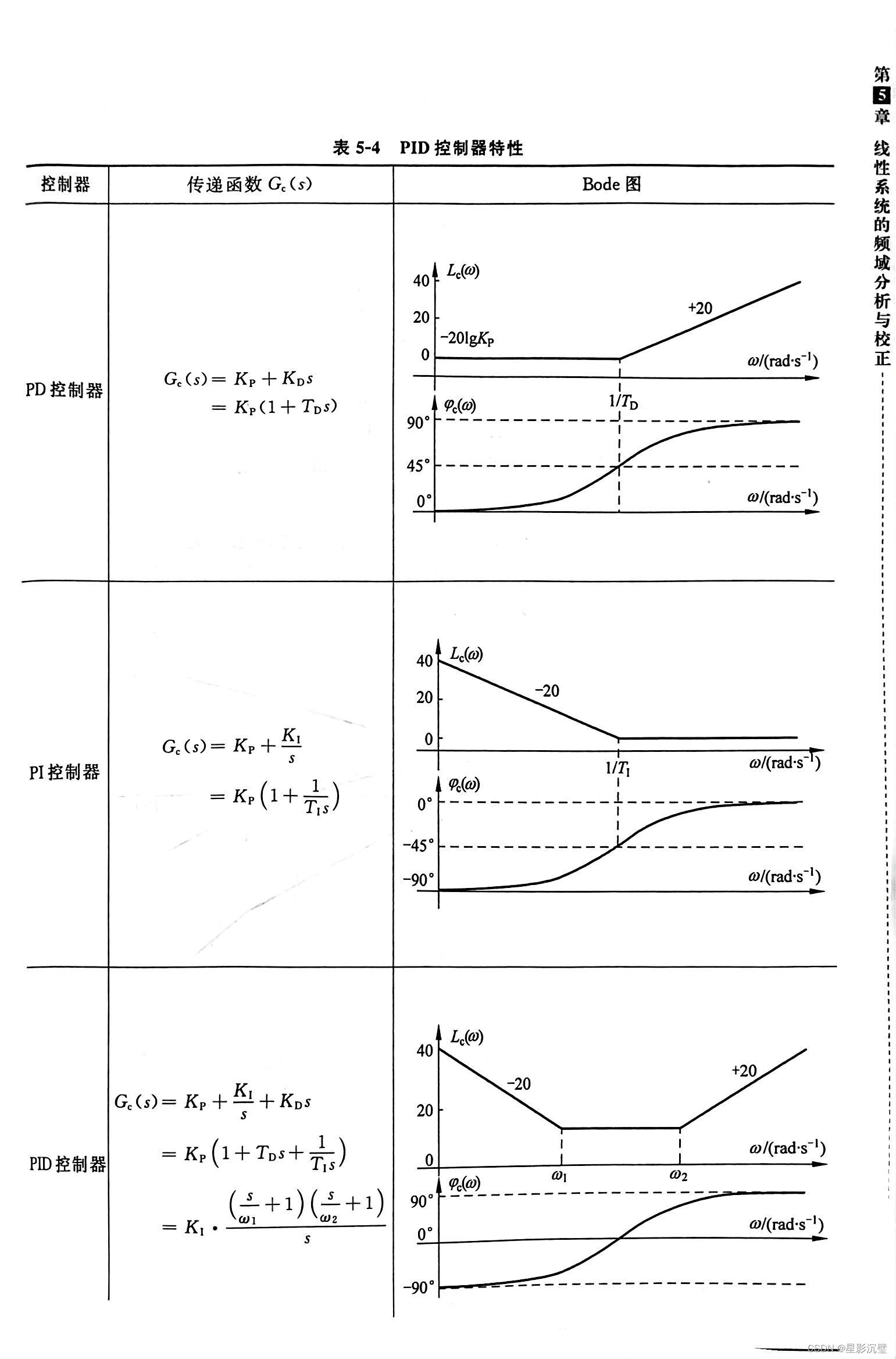图1

1.P控制（比例控制）和P控制器

1.P控制

这里的P取之英文单词Porportional的首字母译为比例的。

在ros小车循迹中的转向和转向偏差要成比例这就是P比例控制：

图2

小车循迹时，我们希望它的速度是平行于道路的，且始终位于道路中心，但因为误差的原因我们无法保证按照理想运行，因此我们按照比例控制来矫正。

1.核心思想：

$e(t)=r(t)-x(t)$ ,理论值减实际值得的误差。

误差越大，用于矫正误差的输入就越大。

2.公式：

$u(t)=K_{p}*e(t)$

2.P控制器

1.核心思想：

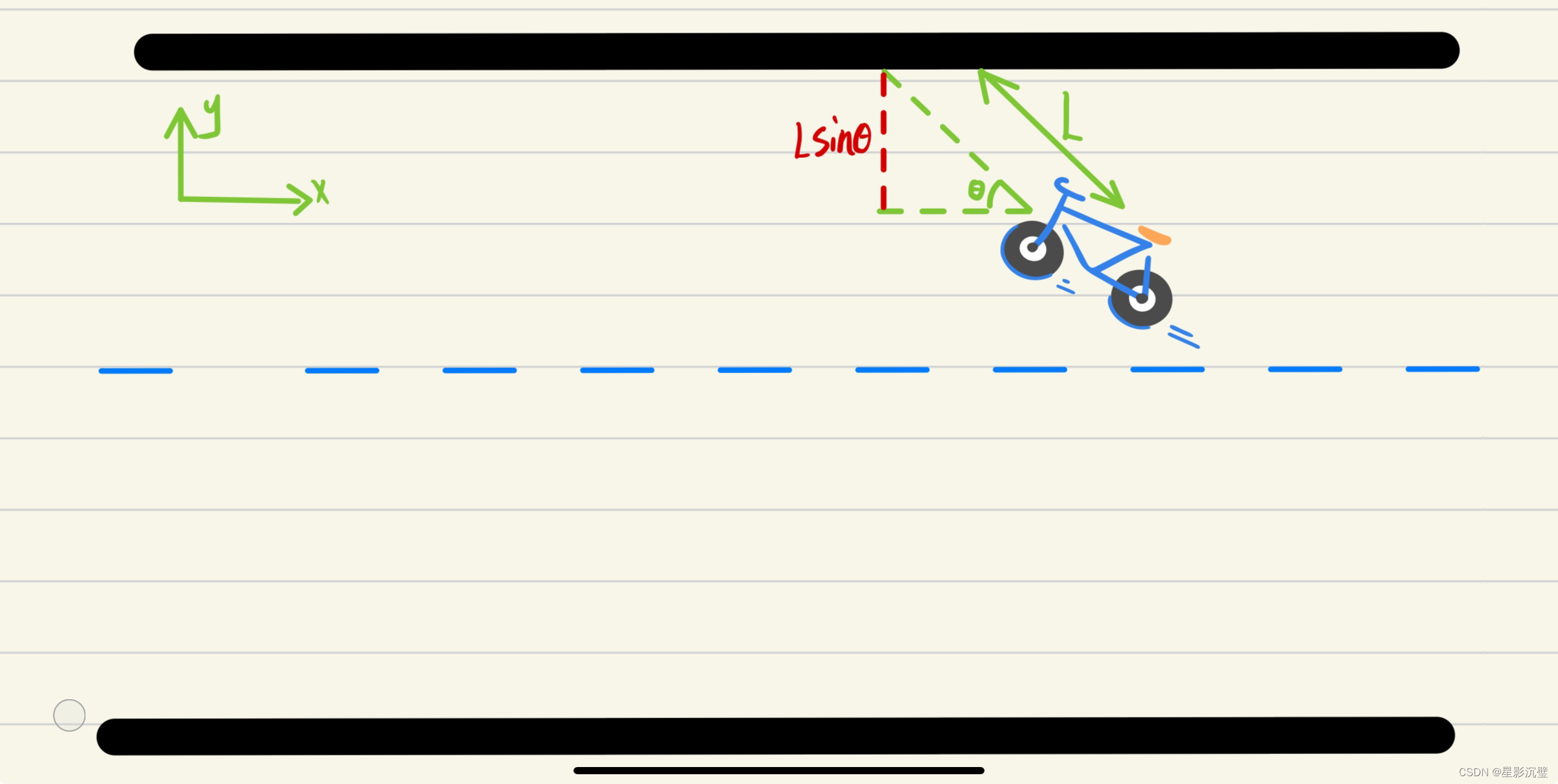图3

当前小车的运动状态如上图蓝线为道路中间线，当我们保证小车速度不变，我们需要的转向角为 $\theta$ ，我们的目的是要保证小车运动在道路中间 $y=0$ ， $\theta =0$ 也就是 $L*sin(\theta )=0$ 。

再结合图2我们就可以得到 $e(t)=-(y+L*sin(\theta ))$

注意：小车的运动方向会影响 $y$ 和 $\theta$ 的取值，受坐标系构建的影响。

1.左转： $y> 0$ ：小车在道路右边——>左转： $\theta <0$

$L*sin(\theta )$ ：小车左转L米——>左转： $\theta <0$

2.右转： $y< 0$ ：小车在道路左边——>右转： $\theta >0$

$L*sin(\theta )$ ：小车右转L米——>右转： $\theta >0$

2.转向角度：

$\theta _{p}=K*e(t)=K_{p}*(-y-L*sin(\theta ))$

小车应用P控制器的运动轨迹：

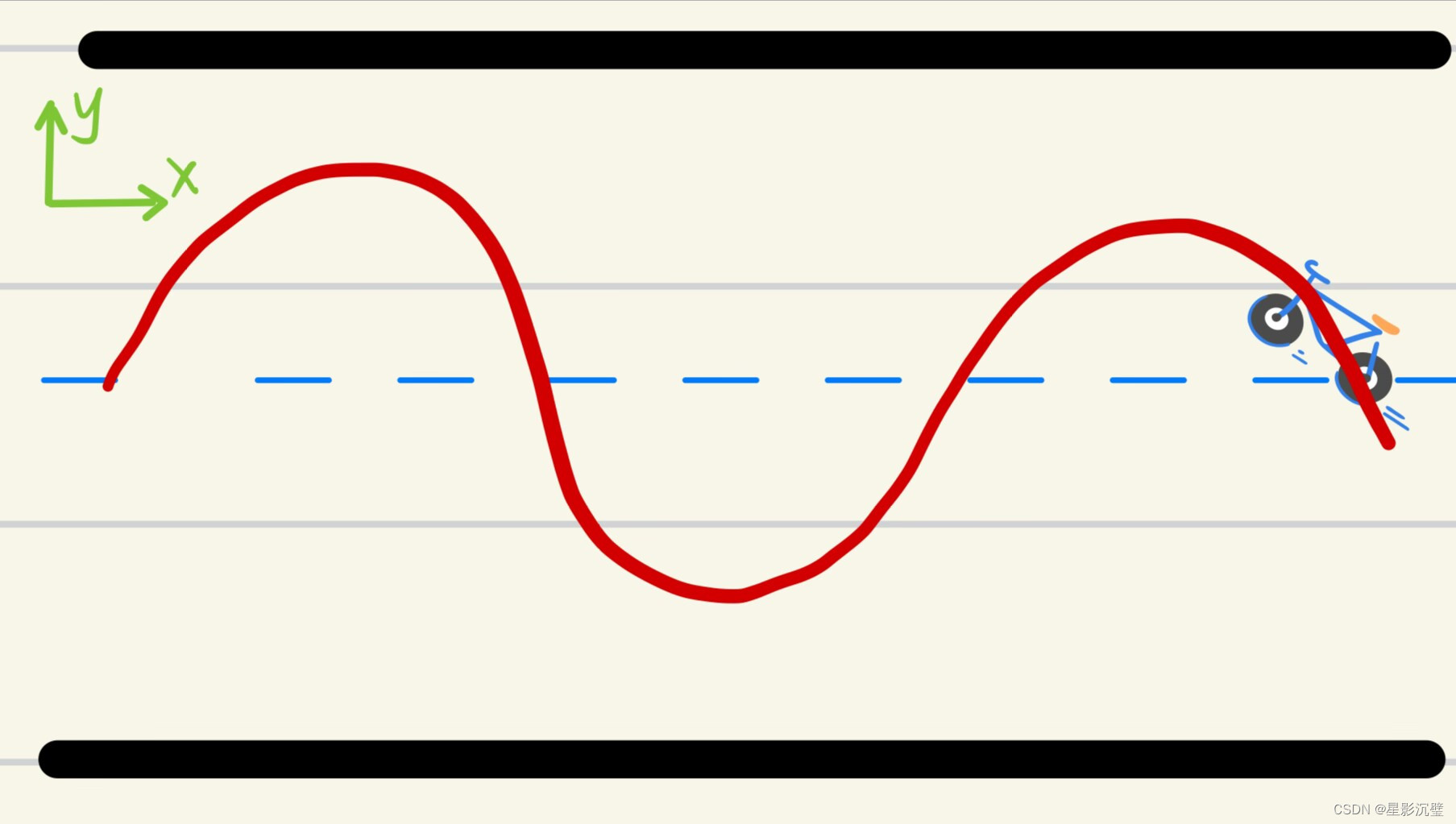图4

2.D控制（微分控制）与PD控制器

1.D控制

这里的D取之英文单词Derivativel的首字母译为微分的。

观看图4可知道仅引入P控制时，我们的小车会在中心线附近摆动，为了出现这种超调现象，我们需要更快的做出调整反应。这时我们引入了D控制，D控制具有超前矫正的作用。

1.核心思想：

D控制预测反馈误差信号 $e(t)$ 的变化趋势（预测基于误差的导数增益）。这里的 $e(t)$ 和P控制里面的 $e(t)$ 是同一个。

2.公式：

$u(t)=K_{p}*\frac{d}{dt}e(t)$

2.PD控制器

1.核心思想

D控制和P控制共同组成了PD控制。

2.转向角度

$\theta _{p}=K_{p}*e(t)+K_{p}*\frac{d}{dt}e(t)=K_{p}*(-y-L*sin(\theta ))+K_{p}*\frac{d}{dt}(-y-L*sin(\theta ))$

小车PD控制运动轨迹：

图5

3.I控制（积分控制）和PID控制器

1.I控制

这里的I取之英文单词Integral的首字母译为积分的。I控制具有滞后和稳定作用。

1.核心思想：

稳态误差随时间积累，I控制提高系统稳定精度。

2.公式：

$u(t)=K_{i}\int_{0}^{t}e(t)dt$ ，这里的 $e(t)$ 和P控制里面的 $e(t)$ 是同一个。

2.PID控制器

1.核心思想：

I控制加入PD控制，会得到PID控制

2.转向角度：

$\theta _{pi}=K_{p}*e(t)+K_{i}\int_{0}^{t}e(t)dt+K_{p}*\frac{d}{dt}e(t)$

误差牺牲 $e(t)=-(y+L*sin(\theta ))$

小车PID控制运动轨迹（红色为PID控制器的运动轨迹，紫色是PD控制器的运动轨迹）：

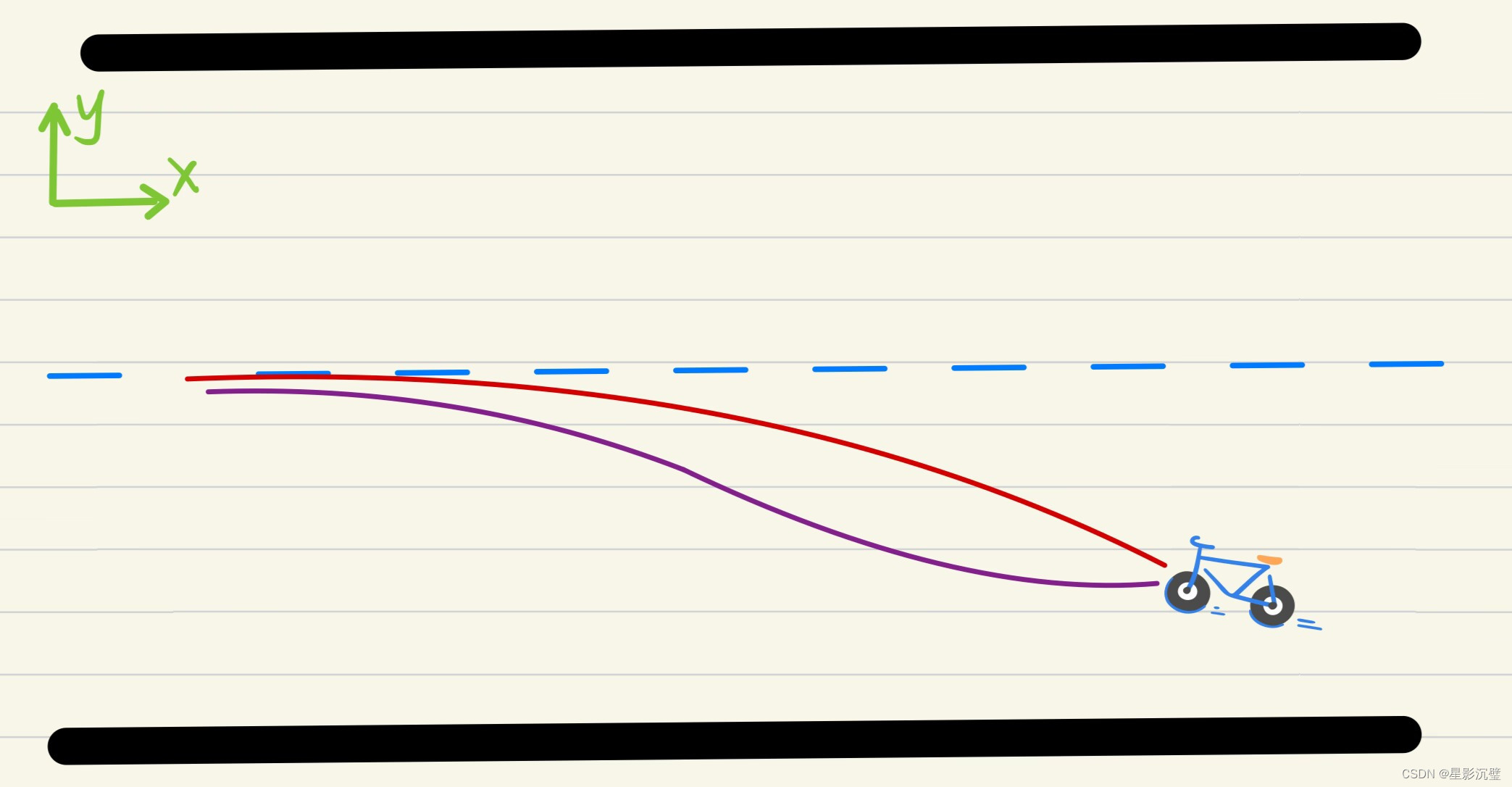图6

4.结尾

好了本篇博客到此就基本结束了，其实本来还应该有个PI控制器的，但我们的核心是PID控制器嘛，所以能得出PID控制器就好了，现在回头看PID的图1，会不会有新的思考？

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1632224.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！