【算法5.1】背包问题 - 01背包（至多最大价值、至少最小价值）

news2024/11/20 8:33:00

至少模板和至多模板的两大区别

1、至多模板

2、至少模板

2. 01背包 - 至多模板 - 体积至多j，总价值最大

1、朴素做法 - 二维dp

2、优化 - 一维dp

4700. 何以包邮？ - 至少模板 - 价值至少j，总价值最小

至少模板和至多模板的两大区别

初始化不同：
至多模板求的是最大值，所以初始化为f[0~m]=0
至少模板求的是最小值，所以初始化为f[0]=0 f[1~m]=0x3f3f3f3f
j 循环范围不同：
至多模板 for(int j=m;j>=w[i];j--) f[j] = max(f[j] , f[ j-w[i] ] + w[i])
至少模板 for(int j=m;j>=0;j--) f[j] = min(f[j] , f[ max(j-w[i] , 0) ] + w[i])

1、至多模板

class Main
{
    static int N=1010;
    static int[] v=new int[N],w=new int[N];
    static int[] f=new int[N];
    
    //f[j] 总体积至多j的情况下，最大价值
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),m=sc.nextInt();
        for(int i=1;i<=n;i++) {v[i]=sc.nextInt();w[i]=sc.nextInt();}
        
        f[0]=0; //初始化 不选物品 总价值为0

        for(int i=1;i<=n;i++)
            for(int j=m;j>=v[i];j--)
                f[j]=Math.max(f[j],f[j-v[i]]+w[i]);

        System.out.print(f[m]);
    }
}

2、至少模板

class Main
{
    static int N=35,M=30*10000+10;
    static int[] w=new int[N];
    static int[] f=new int[M];
    static int n,x;
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        n=sc.nextInt();x=sc.nextInt();
        for(int i=1;i<=n;i++)  w[i]=sc.nextInt(); 
        
        Arrays.fill(f,0x3f3f3f3f);
        f[0]=0;
        for(int i=1;i<=n;i++)
            for(int j=x;j>=0;j--)
                f[j]=Math.min(f[j],f[Math.max(j-w[i],0)]+w[i]);
        
        System.out.print(f[x]);
    }
}

2. 01背包 - 至多模板 - 体积至多j，总价值最大

2. 01背包问题 - AcWing题库

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

1、朴素做法 - 二维dp

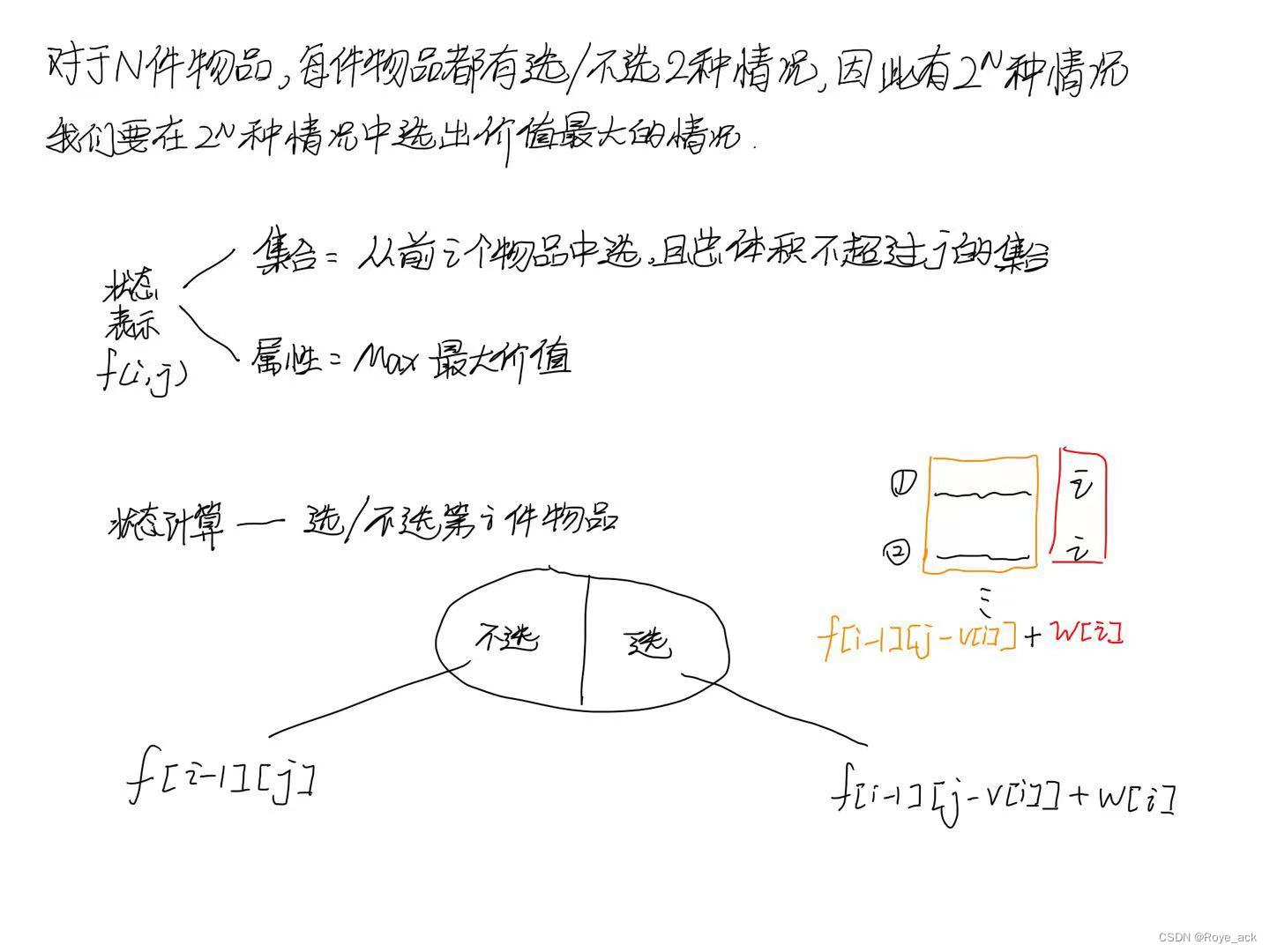
状态定义： $f[i][j]$ 表示只选前i件物品，总体积不超过j 的情况下的最大价值
则答案就是f[n][m]

（当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0] = 0开始决策，有 N 件物品，则需要 N 次决策，每一次对第 i 件物品的决策，状态f[i][j]不断由之前的状态更新而来）

j < v[i]，当前背包容量不够，不能选第i件物品，因此前i个物品最优解即为前 i−1个物品最优解

$f[i][j]=f[i-1][j]$

j ≥ v[i]，背包容量够，因此需要决策选与不选第i个物品

选 $f[i][j]=f[i-1][j-v[i]]+w[i]$ （前i-1个物品且体积给第i件物体留个空+第i件物品的价值
不选 $f[i][j]=f[i-1][j]$
最后要求最大价值，则max（选，不选）

import java.util.*;

class Main
{
    static int N=1010;
    static int[] v=new int[N],w=new int[N];
    static int[][] f=new int[N][N];
    
    //f[i][j] 只选前i件物品，总体积不超过j的情况下，最大价值
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),m=sc.nextInt();
        for(int i=1;i<=n;i++)
        {
            v[i]=sc.nextInt();
            w[i]=sc.nextInt();
        }
        
        f[0][0]=0; //初始化 不选物品 总价值为0
        for(int i=1;i<=n;i++)
            for(int j=0;j<=m;j++)
            {
                f[i][j]=f[i-1][j]; //不选的情况
                if(j>=v[i]) //可以装得下的情况，max(不选，选)
                    f[i][j]=Math.max(f[i][j],f[i-1][j-v[i]]+w[i]);
            }
        System.out.print(f[n][m]);
    }
}

2、优化 - 一维dp

可以看出f[i][~]只依赖于f[i-1][~]，所以根本没必要保留之前的f[i-2][~]等状态值

状态定义： $f[j]$ N 件物品，背包容量j情况下的最大价值

一维情况下枚举背包容量 j 需要逆序大的先更新，小的再更新

import java.util.*;

class Main
{
    static int N=1010;
    static int[] v=new int[N],w=new int[N];
    static int[] f=new int[N];
    
    //f[j] 总体积恰好为j的情况下，最大价值
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),m=sc.nextInt();
        for(int i=1;i<=n;i++)
        {
            v[i]=sc.nextInt();
            w[i]=sc.nextInt();
        }
        
        f[0]=0; //初始化 不选物品 总价值为0
        for(int i=1;i<=n;i++)
            for(int j=m;j>=v[i];j--)
                f[j]=Math.max(f[j],f[j-v[i]]+w[i]);
        System.out.print(f[m]);
    }
}