目录
- 1.AMI的的编解码原理
- 1.1 AMI编码原理
- 1.2 AMI解码原理
- 2.AMI编解码的代码
- 3.AMI编解码结果图
- 4.AMI的误码率曲线
- 4.1 原理
- 4.2 AMI的误码率曲线代码
- 4.3 误码率曲线图
1.AMI的的编解码原理
1.1 AMI编码原理
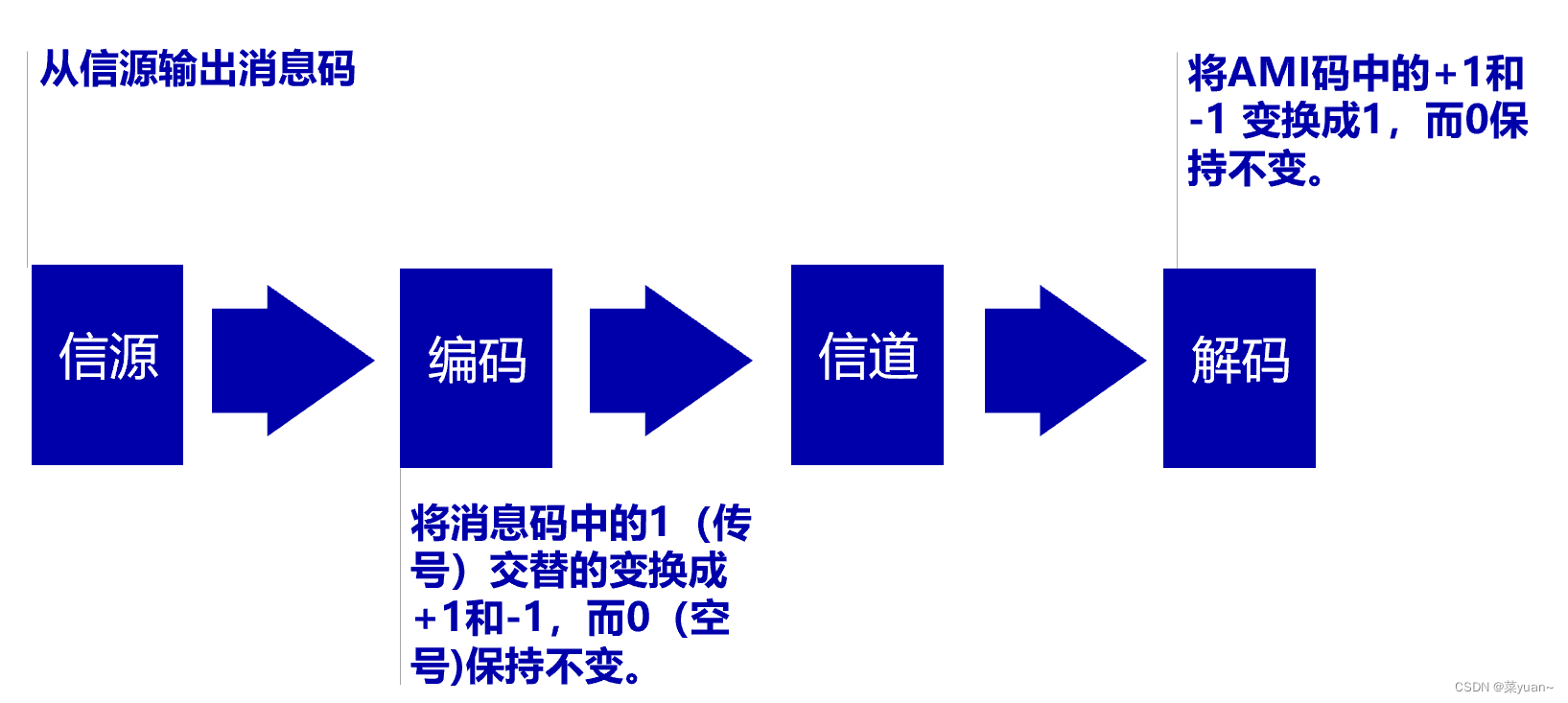
如下图所示,AMI的编码原理:将原始码元的1转换成1,0转换成-1。
1.2 AMI解码原理
AMI解码原理:将AMI码元中的1转换成1,-1转换成0。
如果是经过信道后的AMI码元,那么解码之前先要经过低通滤波器,然后抽样判决后,恢复出AMI码,然后再进行解码。
2.AMI编解码的代码
clear all; % 清除所有变量
close all; % 关闭所有窗口
clc; % 清屏
%% 基本参数
M=10; % 产生码元数
L=100; % 每码元复制L次,每个码元采样次数
Ts=0.001; % 每个码元的宽度,即码元的持续时间
Rb=1/Ts; % 码元速率1K
dt=Ts/L; % 采样间隔
TotalT=M*Ts; % 总时间
t=0:dt:TotalT-dt; % 时间
Fs=1/dt; % 采样间隔的倒数即采样频率
%% 产生单极性波形
wave=randi([0,1],1,M); % 产生二进制随机码,M为码元个数
%% AMI编码,将原码中的1转换成1,0转换成-1
for i=1:M
if wave(i)==1
ami(i)=1;
else
ami(i)=-1;
end
end
fz=ones(1,L); % 定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:); % 将原来wave的第一行复制L次,称为L*M的矩阵
jidai=reshape(x1,1,L*M); % 产生单极性不归零矩形脉冲波形,将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
x2=ami(fz,:); % 将原来ami的第一行复制L次,称为L*M的矩阵
ami_tz=reshape(x2,1,L*M); % 将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
%% 绘制波形
figure(1); % 绘制第1幅图
subplot(311); % 窗口分割成3*1的,当前是第1个子图
plot(t,jidai,'LineWidth',2);% 绘制基带码元波形,线宽为2
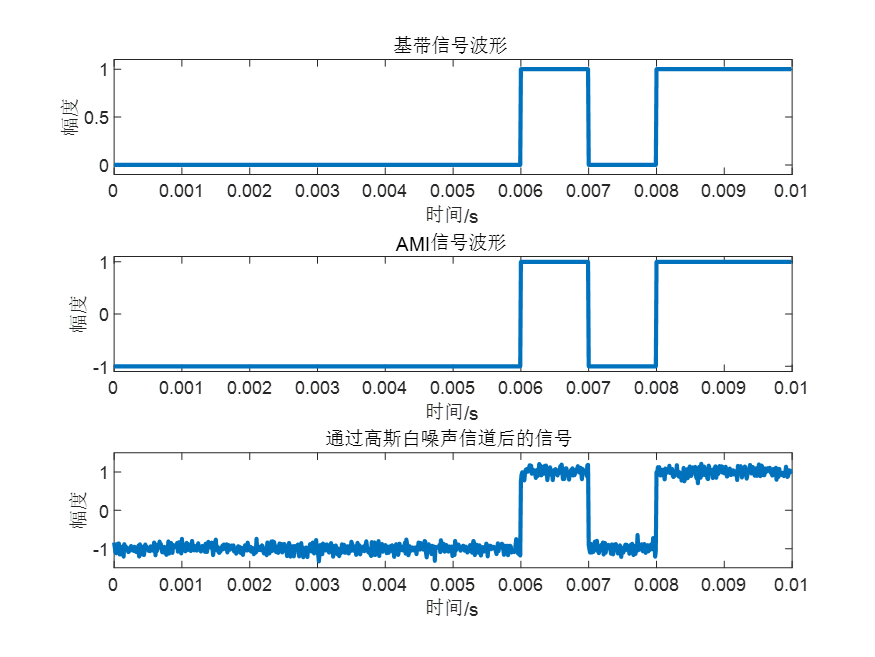
title('基带信号波形'); % 标题
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
axis([0,TotalT,-0.1,1.1]) % 坐标范围限制
subplot(312) % 窗口分割成3*1的,当前是第2个子图
plot(t,ami_tz,'LineWidth',2);% 绘制ami的波形
title('AMI信号波形') % 标题
axis([0,TotalT,-1.1,1.1]); % 坐标范围限制
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
%% 信号经过高斯白噪声信道
tz=awgn(ami_tz,20); % 信号ami_tz中加入白噪声,信噪比为SNR=20dB
subplot(313); % 窗口分割成3*1的,当前是第1个子图
plot(t,tz,'LineWidth',2); % 绘制2ASK信号加入白噪声的波形
axis([0,TotalT,-1.5,1.5]); % 坐标范围设置
title('通过高斯白噪声信道后的信号');% 标题
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
%% 解码部分
%% 加噪信号经过滤波器
% 低通滤波器设计
fp=2*Rb; % 低通滤波器截止频率,乘以2是因为下面要将模拟频率转换成数字频率wp=Rb/(Fs/2)
b=fir1(30, fp/Fs, boxcar(31));% 生成fir滤波器系统函数中分子多项式的系数
% fir1函数三个参数分别是阶数,数字截止频率,滤波器类型
% 这里是生成了30阶(31个抽头系数)的矩形窗滤波器
[h,w]=freqz(b, 1,512); % 生成fir滤波器的频率响应
% freqz函数的三个参数分别是滤波器系统函数的分子多项式的系数,分母多项式的系数(fir滤波器分母系数为1)和采样点数(默认)512
lvbo=fftfilt(b,tz); % 对信号进行滤波,tz是等待滤波的信号,b是fir滤波器的系统函数的分子多项式系数
figure(2); % 绘制第2幅图
subplot(411); % 窗口分割成4*1的,当前是第1个子图
plot(w/pi*Fs/2,20*log(abs(h)),'LineWidth',2); % 绘制滤波器的幅频响应
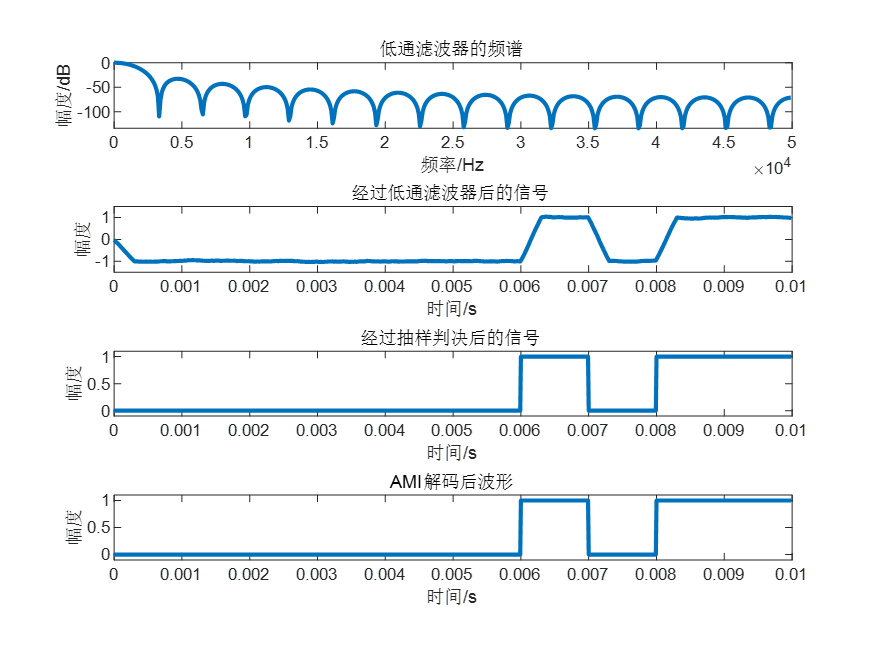
title('低通滤波器的频谱'); % 标题
xlabel('频率/Hz'); % x轴标签
ylabel('幅度/dB'); % y轴标签
subplot(412) % 窗口分割成4*1的,当前是第2个子图
plot(t,lvbo,'LineWidth',2); % 绘制经过低通滤波器后的信号
axis([0,TotalT,-1.5,1.5]); % 设置坐标范围
title("经过低通滤波器后的信号");% 标题
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
%% 抽样判决
pdst=1*(lvbo>0); % 滤波后的向量的每个元素和0进行比较,大于0为1,否则为0
% 取码元中间时刻值为判决值
panjue=[];
for j=(L/2):L:(L*M)
if pdst(j)>0
panjue=[panjue,1];
else
panjue=[panjue,0];
end
end
x3=panjue(fz,:); % 将原来panjue的第一行复制L次,称为L*M的矩阵
huifu=reshape(x3,1,L*M); % 将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
subplot(413) % 窗口分割成4*1的,当前是第3个子图
plot(t,huifu,'LineWidth',2) % 画出经过抽样判决后的信号
axis([0,TotalT,-0.1,1.1]); % 设置坐标范用
title("经过抽样判决后的信号")% 标题
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
%% AMI解码,1对应转换为1,-1转换成0
for i=1:M
if panjue(i)==1
dout(i)=1;
else
dout(i)=0;
end
end
x4=dout(fz,:); % 将原来dout的第一行复制L次,称为L*M的矩阵
dout_wave=reshape(x4,1,L*M);% 将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
subplot(414) % 窗口分割成4*1的,当前是第4个子图
plot(t,dout_wave,'LineWidth',2)% 画出经过抽样判决后的信号
axis([0,TotalT,-0.1,1.1]); % 设置坐标范用
title("AMI解码后波形") % 标题
xlabel('时间/s'); % x轴标签
ylabel('幅度'); % y轴标签
%% 绘制频谱
%% 基带信号频谱
T=t(end); % 时间
df=1/T; % 频谱分辨率
N=length(jidai); % 采样长度
f=(-N/2:N/2-1)*df; % 频率范围
mf=fftshift(abs(fft(jidai)));%对信源信号采用快速傅里叶变换并移到矩阵中心
figure(3) % 绘制第3幅图
subplot(211); % 窗口分割成2*1的,当前是第1个子图
plot(f,mf,'LineWidth',2); % 绘制信源频谱波形
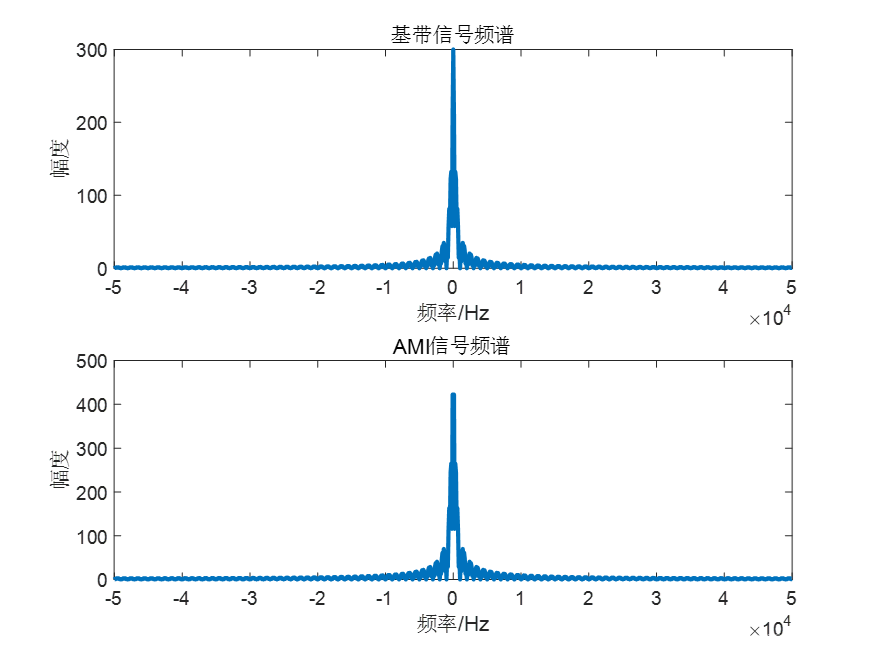
title("基带信号频谱"); % 标题
xlabel('频率/Hz'); % x轴标签
ylabel('幅度'); % y轴标签
%% AMI信号频谱
sf=fftshift(abs(fft(ami_tz))); % 对AMI信号采用快速傅里叶变换并将0-fs频谱移动到-fs/2-fs/2
subplot(212) % 窗口分割成2*1的,当前是第1个子图
plot(f,sf,'LineWidth',2) % 绘制调制信号频谱
title("AMI信号频谱") % 标题
xlabel('频率/Hz'); % x轴标签
ylabel('幅度'); % y轴标签
%% 加入噪声后的频谱
mmf=fftshift(abs(fft(tz))); % 对信号采用快速傅里叶变换并移到矩阵中心
figure(4) % 绘制第4幅图
subplot(211); % 窗口分割成2*1的,当前是第1个子图
plot(f,mmf,'LineWidth',2) % 画出乘以相干载波后的频谱
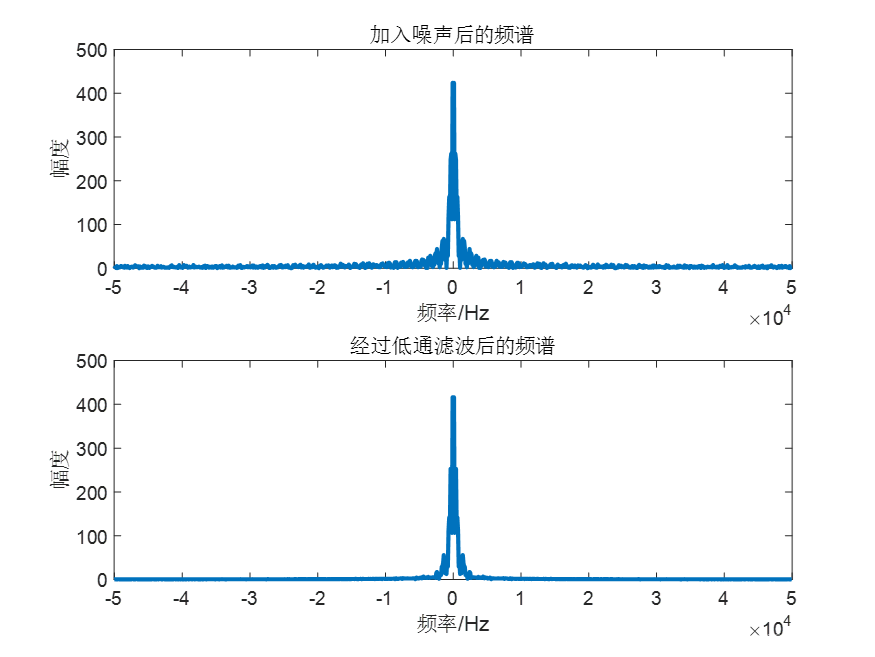
title("加入噪声后的频谱") % 标题
xlabel('频率/Hz'); % x轴标签
ylabel('幅度'); % y轴标签
%% 经过低通滤波后的频谱
dmf=fftshift(abs(fft(lvbo)));%对低通滤波信号采用快速傅里叶变换并移到矩阵中心
subplot(212); % 窗口分割成2*1的,当前是第2个子图
plot(f,dmf,'LineWidth',2) % 画出经过低通滤波后的频谱
title("经过低通滤波后的频谱");% 标题
xlabel('频率/Hz'); % x轴标签
ylabel('幅度'); % y轴标签
3.AMI编解码结果图
4.AMI的误码率曲线
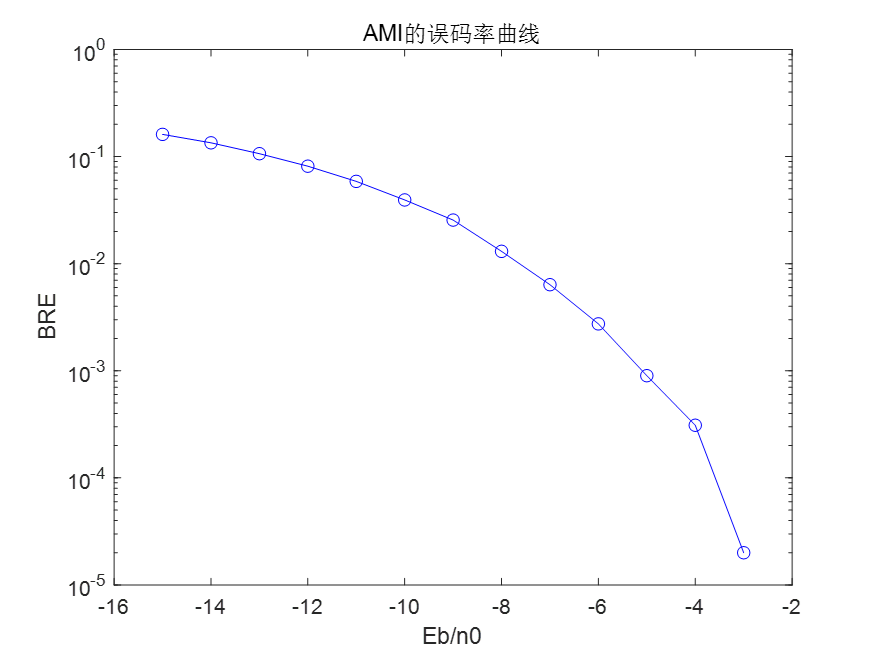
4.1 原理
计算某信噪比下的错误的码元个数,然后除以总码元个数,即该信噪比下的误码率。然后更改信噪比,计算新的误码率,一个信噪比对应一个误码率,连点成线。
4.2 AMI的误码率曲线代码
clear all; % 清除所有变量
close all; % 关闭所有窗口
clc; % 清屏
%% 基本参数
M=100000; % 产生码元数
L=100; % 每码元复制L次,每个码元采样次数
Ts=0.001; % 每个码元的宽度,即码元的持续时间
Rb=1/Ts; % 码元速率1K
dt=Ts/L; % 采样间隔
TotalT=M*Ts; % 总时间
t=0:dt:TotalT-dt; % 时间
Fs=1/dt; % 采样间隔的倒数即采样频率
%% 产生单极性波形
wave=randi([0,1],1,M); % 产生二进制随机码,M为码元个数
%% AMI编码,将原码中的1转换成1,0转换成-1
for i=1:M
if wave(i)==1
ami(i)=1;
else
ami(i)=-1;
end
end
fz=ones(1,L); % 定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:); % 将原来wave的第一行复制L次,称为L*M的矩阵
jidai=reshape(x1,1,L*M); % 产生单极性不归零矩形脉冲波形,将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
x2=ami(fz,:); % 将原来ami的第一行复制L次,称为L*M的矩阵
ami_tz=reshape(x2,1,L*M); % 将刚得到的L*M矩阵,按列重新排列形成1*(L*M)的矩阵
%% 信号经过高斯白噪声信道
EbN0_dB = -15:1:5;
for i=1:21
tz=awgn(ami_tz,EbN0_dB(i)); % 信号ami_tz中加入白噪声
%% 解码部分
%% 加噪信号经过滤波器
% 低通滤波器设计
fp=2*Rb; % 低通滤波器截止频率,乘以2是因为下面要将模拟频率转换成数字频率wp=Rb/(Fs/2)
b=fir1(30, fp/Fs, boxcar(31));% 生成fir滤波器系统函数中分子多项式的系数
% fir1函数三个参数分别是阶数,数字截止频率,滤波器类型
% 这里是生成了30阶(31个抽头系数)的矩形窗滤波器
[h,w]=freqz(b, 1,512); % 生成fir滤波器的频率响应
% freqz函数的三个参数分别是滤波器系统函数的分子多项式的系数,分母多项式的系数(fir滤波器分母系数为1)和采样点数(默认)512
lvbo=fftfilt(b,tz); % 对信号进行滤波,tz是等待滤波的信号,b是fir滤波器的系统函数的分子多项式系数
%% 抽样判决
pdst=1*(lvbo>0); % 滤波后的向量的每个元素和0进行比较,大于0为1,否则为0
% 取码元中间时刻值为判决值
panjue=[];
for j=(L/2):L:(L*M)
if pdst(j)>0
panjue=[panjue,1];
else
panjue=[panjue,0];
end
end
%% AMI解码,1对应转换为1,-1转换成0
for k=1:M
if panjue(k)==1
dout(k)=1;
else
dout(k)=0;
end
end
% 计算错误码元数,然后除以总码元数得到误码率
error_num=length(find(dout~=wave));
error_rate(i)=error_num/M;
end
figure(1)
semilogy(EbN0_dB,error_rate,'-ob');% 绘制误码率曲线
xlabel('Eb/n0'); % x轴标签
ylabel('BRE'); % y轴标签
title('AMI的误码率曲线') % 标题
4.3 误码率曲线图