EquiBind模型源码分析

使用提供的模型权重来预测你自己的蛋白质配体对的结合结构

• 第 1 步:你需要什么作为输入
  mol2或.sdf或.pdbqt或.pdb格式的配体文件，其名称包含字符串配体(配体文件应包含所有氢)。
  .pdb格式的受体文件，其名称包含字符串protein。我们运行reduce训练我们的蛋白质。也许你也想运行自己的蛋白质。

Reduce - 在 PDB 文件中添加和修正氢的工具

加载数据

读取配体信息

 读取配体sdf文件信息
lig = read_molecule(os.path.join(args.inference_path, name, lig_name), sanitize=True)#

读取受体信息

主要包括全原子的三维坐标， CA， N， C主干上原子的三维坐标

## 读取受体的信息
rec, rec_coords, c_alpha_coords, n_coords, c_coords = get_receptor_inference(rec_path)

Equibind数据处理

预处理受体信息

rec: 受体对象
rec_coords 受体全原子坐标
c_alpha_coords CA坐标
n_coords N坐标
c_coords C坐标
use_rec_atoms是否使用残基原子
rec_graph_radius
surface_max_neighbors 最大邻节点个数
surface_graph_cutoff 距离cut off 多少埃
surface_mesh_cutoff
c_alpha_max_neighbors CA最大邻节点

rec_graph = get_rec_graph(rec, rec_coords, c_alpha_coords, n_coords, c_coords,
                                  use_rec_atoms=dp['use_rec_atoms'], rec_radius=dp['rec_graph_radius'], #
                                  surface_max_neighbors=dp['surface_max_neighbors'],
                                  surface_graph_cutoff=dp['surface_graph_cutoff'],
                                  surface_mesh_cutoff=dp['surface_mesh_cutoff'],
                                  c_alpha_max_neighbors=dp['c_alpha_max_neighbors'])

将蛋白表示为结构

def get_calpha_graph(rec, c_alpha_coords, n_coords, c_coords, cutoff=20, max_neighbor=None):
    ################## Extract 3D coordinates and n_i,u_i,v_i vectors of representative residues 提取代表性残基的 3D 坐标和 n_i,u_i,v_i 向量################
    residue_representatives_loc_list = []
    n_i_list = []
    u_i_list = []
    v_i_list = []
    for i, residue in enumerate(rec.get_residues()):
        n_coord = n_coords[i] # N原子坐标
        c_alpha_coord = c_alpha_coords[i] # CA原子坐标
        c_coord = c_coords[i] # C原子坐标
        u_i = (n_coord - c_alpha_coord) / np.linalg.norm(n_coord - c_alpha_coord) # N-CA 向量
        t_i = (c_coord - c_alpha_coord) / np.linalg.norm(c_coord - c_alpha_coord) # C-CA 向量
        n_i = np.cross(u_i, t_i) / np.linalg.norm(np.cross(u_i, t_i)) # N-CA 与 C-CA 叉乘法向量
        v_i = np.cross(n_i, u_i) # N-CA 与 C-CA 叉乘法向量
        assert (math.fabs(
            np.linalg.norm(v_i) - 1.) < 1e-5), "protein utils protein_to_graph_dips, v_i norm larger than 1"
        n_i_list.append(n_i)
        u_i_list.append(u_i)
        v_i_list.append(v_i)
        residue_representatives_loc_list.append(c_alpha_coord)

    residue_representatives_loc_feat = np.stack(residue_representatives_loc_list, axis=0)  # (N_res, 3) CA原子坐标
    n_i_feat = np.stack(n_i_list, axis=0)
    u_i_feat = np.stack(u_i_list, axis=0)
    v_i_feat = np.stack(v_i_list, axis=0)
    num_residues = len(c_alpha_coords)
    if num_residues <= 1:
        raise ValueError(f"rec contains only 1 residue!")

    ################### Build the k-NN graph ##############################
    assert num_residues == residue_representatives_loc_feat.shape[0]
    assert residue_representatives_loc_feat.shape[1] == 3
    distances = spa.distance.cdist(c_alpha_coords, c_alpha_coords) #计算距离， 默认欧几里得距离
    src_list = []
    dst_list = []
    dist_list = []
    mean_norm_list = []
    for i in range(num_residues):
        dst = list(np.where(distances[i, :] < cutoff)[0]) # 距离小于30的
        dst.remove(i)
        if max_neighbor != None and len(dst) > max_neighbor: # 最大的邻节点过滤,
            dst = list(np.argsort(distances[i, :]))[1: max_neighbor + 1]
        if len(dst) == 0:
            dst = list(np.argsort(distances[i, :]))[1:2]  # choose second because first is i itself
            log(
                f'The c_alpha_cutoff {cutoff} was too small for one c_alpha such that it had no neighbors. So we connected it to the closest other c_alpha')
        assert i not in dst
        src = [i] * len(dst)
        src_list.extend(src)# 
        dst_list.extend(dst)#
        valid_dist = list(distances[i, dst])
        dist_list.extend(valid_dist)
        valid_dist_np = distances[i, dst]
        sigma = np.array([1., 2., 5., 10., 30.]).reshape((-1, 1))#
        weights = softmax(- valid_dist_np.reshape((1, -1)) ** 2 / sigma, axis=1)  # (sigma_num, neigh_num)
        assert weights[0].sum() > 1 - 1e-2 and weights[0].sum() < 1.01
        diff_vecs = residue_representatives_loc_feat[src, :] - residue_representatives_loc_feat[
                                                               dst, :]  # (neigh_num, 3)起始就是向量
        mean_vec = weights.dot(diff_vecs)  # (sigma_num, neigh_num) @ (neigh_num, 3)->(sigma_num, 3)
        denominator = weights.dot(np.linalg.norm(diff_vecs, axis=1))  # (sigma_num,)
        mean_vec_ratio_norm = np.linalg.norm(mean_vec, axis=1) / denominator  # (sigma_num,)
        mean_norm_list.append(mean_vec_ratio_norm)
    assert len(src_list) == len(dst_list)
    assert len(dist_list) == len(dst_list)
    graph = dgl.graph((torch.tensor(src_list), torch.tensor(dst_list)), num_nodes=num_residues, idtype=torch.int32)

    graph.ndata['feat'] = rec_residue_featurizer(rec)
    graph.edata['feat'] = distance_featurizer(dist_list, divisor=4)  # avg distance = 7. So divisor = (4/7)*7 = 4

    # Loop over all edges of the graph and build the various p_ij, q_ij, k_ij, t_ij pairs 在图的所有边上循环并构建各种p_ij、q_ij、k_ij、t_ij对
    edge_feat_ori_list = []
    for i in range(len(dist_list)):
        src = src_list[i]
        dst = dst_list[i]
        # place n_i, u_i, v_i as lines in a 3x3 basis matrix
        basis_matrix = np.stack((n_i_feat[dst, :], u_i_feat[dst, :], v_i_feat[dst, :]), axis=0)
        p_ij = np.matmul(basis_matrix,
                         residue_representatives_loc_feat[src, :] - residue_representatives_loc_feat[
                                                                    dst, :])
        q_ij = np.matmul(basis_matrix, n_i_feat[src, :])  # shape (3,)
        k_ij = np.matmul(basis_matrix, u_i_feat[src, :])
        t_ij = np.matmul(basis_matrix, v_i_feat[src, :])
        s_ij = np.concatenate((p_ij, q_ij, k_ij, t_ij), axis=0)  # shape (12,)
        edge_feat_ori_list.append(s_ij)
    edge_feat_ori_feat = np.stack(edge_feat_ori_list, axis=0)  # shape (num_edges, 4* 3)
    edge_feat_ori_feat = torch.from_numpy(edge_feat_ori_feat.astype(np.float32))
    graph.edata['feat'] = torch.cat([graph.edata['feat'], edge_feat_ori_feat], axis=1)  # (num_edges, 27)

    residue_representatives_loc_feat = torch.from_numpy(residue_representatives_loc_feat.astype(np.float32))
    graph.ndata['x'] = residue_representatives_loc_feat
    graph.ndata['mu_r_norm'] = torch.from_numpy(np.array(mean_norm_list).astype(np.float32))
    return graph

重点–> 非常重要的处理细节

1. 构建局部坐标
   
   $u_i$是$\alpha -C$原子指向N原子的向量；$t_i$是$\alpha -C$原子指向C原子的向量；
   $n_i$是垂直于$u_i$和$t_i$的向量；$v_i$是垂直于$n_i$和$u_i$的向量
   那么$n_i$、$v_i$和$u_i$两两垂直，构成了一个局部坐标系($u_i,v_i,n_i$)

n_coord = n_coords[i] # N原子坐标
c_alpha_coord = c_alpha_coords[i] # CA原子坐标
c_coord = c_coords[i] # C原子坐标
u_i = (n_coord - c_alpha_coord) / np.linalg.norm(n_coord - c_alpha_coord) # N-CA 向量
t_i = (c_coord - c_alpha_coord) / np.linalg.norm(c_coord - c_alpha_coord) # C-CA 向量
n_i = np.cross(u_i, t_i) / np.linalg.norm(np.cross(u_i, t_i)) # N-CA 与 C-CA 叉乘法向量
v_i = np.cross(n_i, u_i) # N-CA 与 C-CA 叉乘法向量

2. 构建KNN图表示
   受体图 $G^{\prime }=(V^{\prime },E^{\prime })$以残基作为节点，它们的 3D 坐标 $X^{\prime }\in R^{3\times m}$ 由 α-碳位置给出。图中的每个节点都以小于$30\mathring{A}$的距离连接到最近的 10 个其他节点。受体节点特征 $F^{\prime }\in R^{d\times m}$。

    for i in range(num_residues):
        dst = list(np.where(distances[i, :] < cutoff)[0]) # CA与CA距离小于30的
        dst.remove(i)# 移除自己和自己本身
        if max_neighbor != None and len(dst) > max_neighbor: # 最大的邻节点过滤,
            dst = list(np.argsort(distances[i, :]))[1: max_neighbor + 1]
        if len(dst) == 0:
            dst = list(np.argsort(distances[i, :]))[1:2]  # choose second because first is i itself
            log(
                f'The c_alpha_cutoff {cutoff} was too small for one c_alpha such that it had no neighbors. So we connected it to the closest other c_alpha')
        assert i not in dst
        src = [i] * len(dst)# 源节点
        src_list.extend(src)# 
        dst_list.extend(dst)#目标节点
        valid_dist = list(distances[i, dst])
        dist_list.extend(valid_dist)
        valid_dist_np = distances[i, dst]
        sigma = np.array([1., 2., 5., 10., 30.]).reshape((-1, 1))#
        weights = softmax(- valid_dist_np.reshape((1, -1)) ** 2 / sigma, axis=1)  # (sigma_num, neigh_num), 计算目标节点的权重
        assert weights[0].sum() > 1 - 1e-2 and weights[0].sum() < 1.01
        diff_vecs = residue_representatives_loc_feat[src, :] - residue_representatives_loc_feat[
                                                               dst, :]  # (neigh_num, 3)起始就是向量
        mean_vec = weights.dot(diff_vecs)  # (sigma_num, neigh_num) @ (neigh_num, 3)->(sigma_num, 3)
        denominator = weights.dot(np.linalg.norm(diff_vecs, axis=1))  # (sigma_num,) 分母
        mean_vec_ratio_norm = np.linalg.norm(mean_vec, axis=1) / denominator  # (sigma_num,) 旋转均值
        mean_norm_list.append(mean_vec_ratio_norm)
    assert len(src_list) == len(dst_list)
    assert len(dist_list) == len(dst_list)
    graph = dgl.graph((torch.tensor(src_list), torch.tensor(dst_list)), num_nodes=num_residues, idtype=torch.int32)  

同时使用了Surface Aware Node Features

表面接触建模对蛋白质对接很重要。这里设计了一种新的表面特征类型，将靠近蛋白质表面的残基与内部的残基区分开来。如上图所示，蛋白质内部的残基（左）被来自各个方向的矢量所包围，这些矢量相互抵消，而靠近表面的残基（右）只在一个较窄的锥体中有邻居，其孔径取决于表面的局部曲率。

通过上式得到5个表面感知节点特征， λ ∈ { 1. , 2. , 5. , 10. , 30. } \lambda \in \{1.,2.,5.,10.,30.\} λ∈{1.,2.,5.,10.,30.}。

sigma = np.array([1., 2., 5., 10., 30.]).reshape((-1, 1))#
weights = softmax(- valid_dist_np.reshape((1, -1)) ** 2 / sigma, axis=1)  # (sigma_num, neigh_num), 计算目标节点的权重
assert weights[0].sum() > 1 - 1e-2 and weights[0].sum() < 1.01
diff_vecs = residue_representatives_loc_feat[src, :] - residue_representatives_loc_feat[
                                                      dst, :]  # (neigh_num, 3)起始就是向量
mean_vec = weights.dot(diff_vecs)  # (sigma_num, neigh_num) @ (neigh_num, 3)->(sigma_num, 3)
denominator = weights.dot(np.linalg.norm(diff_vecs, axis=1))  # (sigma_num,) 分母
mean_vec_ratio_norm = np.linalg.norm(mean_vec, axis=1) / denominator  # (sigma_num,) 每个残基旋转均值
mean_norm_list.append(mean_vec_ratio_norm)

3. 残基图上特征
   节点特征使用残基类型、sasa(表面溶剂接触面积)和bfactor。

def rec_residue_featurizer(rec):
    feature_list = []
    sr.compute(rec, level="R")# 计算实体的表面辅助功能表面积。
    for residue in rec.get_residues():
        sasa = residue.sasa
        for atom in residue:
            if atom.name == 'CA':
                bfactor = atom.bfactor
        assert not np.isinf(bfactor)
        assert not np.isnan(bfactor)
        assert not np.isinf(sasa)
        assert not np.isnan(sasa)
        feature_list.append([safe_index(allowable_features['possible_amino_acids'], residue.get_resname()),
                             sasa,
                             bfactor])
    return torch.tensor(feature_list, dtype=torch.float32)  # (N_res, 1)

边特征使用具有 15 个不同方差的高斯基函数编码的原子间距离。

• Distance-Based Edge Features
  距离也带有信息，这里使用距离的径向基函数作为边缘特征。
  
  其中$R$和缩放参数 { σ r } 1 ≤ r ≤ R \{\sigma_r\}_{1\leq r \leq R} {σr​}1≤r≤R​是超参，论文中使用的缩放参数为 { 1. 5 x ∣ x = 0 , 1 , 2 , . . . , 14 } \{1.5^x|x=0,1,2,...,14\} {1.5x∣x=0,1,2,...,14},因此，对于每条边有15个基于距离的边特征。

def distance_featurizer(dist_list, divisor) -> torch.Tensor: # 您希望使用一个约数，该约数接近要编码的平均距离的4/7倍
    # you want to use a divisor that is close to 4/7 times the average distance that you want to encode
    length_scale_list = [1.5 ** x for x in range(15)]
    center_list = [0. for _ in range(15)]

    num_edge = len(dist_list)
    dist_list = np.array(dist_list)

    transformed_dist = [np.exp(- ((dist_list / divisor) ** 2) / float(length_scale))
                        for length_scale, center in zip(length_scale_list, center_list)]

    transformed_dist = np.array(transformed_dist).T
    transformed_dist = transformed_dist.reshape((num_edge, -1))
    return torch.from_numpy(transformed_dist.astype(np.float32))

边特征还是用局部骨架方向编码

• Relative Position Edge Features
  边特征$p_{j\to i}$，代表j相对于$i$的相对位置
  
• Relative Orientation Edge Features
  边缘特征$q_{j\to i}$、$k_{j\to i}$和$t_{j\to i}$，表示$j$相对于$i$的相对方向。
  

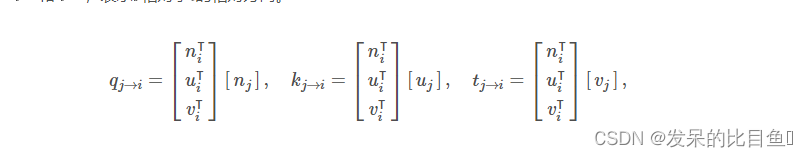
    edge_feat_ori_list = []
    for i in range(len(dist_list)):
        src = src_list[i]
        dst = dst_list[i]
        # place n_i, u_i, v_i as lines in a 3x3 basis matrix
        basis_matrix = np.stack((n_i_feat[dst, :], u_i_feat[dst, :], v_i_feat[dst, :]), axis=0)
        p_ij = np.matmul(basis_matrix,
                         residue_representatives_loc_feat[src, :] - residue_representatives_loc_feat[
                                                                    dst, :])
        q_ij = np.matmul(basis_matrix, n_i_feat[src, :])  # shape (3,)
        k_ij = np.matmul(basis_matrix, u_i_feat[src, :])
        t_ij = np.matmul(basis_matrix, v_i_feat[src, :])
        s_ij = np.concatenate((p_ij, q_ij, k_ij, t_ij), axis=0)  # shape (12,)
        edge_feat_ori_list.append(s_ij)
    edge_feat_ori_feat = np.stack(edge_feat_ori_list, axis=0)  # shape (num_edges, 4* 3)
    edge_feat_ori_feat = torch.from_numpy(edge_feat_ori_feat.astype(np.float32))
    graph.edata['feat'] = torch.cat([graph.edata['feat'], edge_feat_ori_feat], axis=1)  # (num_edges, 27)

预处理配体信息

在配体中，边缘具有以与受体相同的方式编码的特征。这里不具体细讲
原子具有以下特征：原子数;手性;度;形式电荷；隐含价；连接氢的数量；自由基电子的数量；杂化类型；是否在芳环中；它有多少个环；最后，6 个特征表示它是否在大小为 3、4、5、6、7 或 8 的环中。

def get_lig_graph_revised(mol, name, radius=20, max_neighbors=None, use_rdkit_coords=False):
    conf = mol.GetConformer()#前提，导入的原子必须带有坐标信息
    true_lig_coords = conf.GetPositions()
    if use_rdkit_coords:
        try:
            rdkit_coords = get_rdkit_coords(mol).numpy()
            R, t = rigid_transform_Kabsch_3D(rdkit_coords.T, true_lig_coords.T)
            lig_coords = ((R @ (rdkit_coords).T).T + t.squeeze())
            log('kabsch RMSD between rdkit ligand and true ligand is ', np.sqrt(np.sum((lig_coords - true_lig_coords) ** 2, axis=1).mean()).item())
        except Exception as e:
            lig_coords = true_lig_coords
            with open('temp_create_dataset_rdkit_timesplit_no_lig_or_rec_overlap_train.log', 'a') as f:
                f.write('Generating RDKit conformer failed for  \n')
                f.write(name)
                f.write('\n')
                f.write(str(e))
                f.write('\n')
                f.flush()
            print('Generating RDKit conformer failed for  ')
            print(name)
            print(str(e))
    else:
        lig_coords = true_lig_coords
    num_nodes = lig_coords.shape[0]
    assert lig_coords.shape[1] == 3
    distance = spa.distance.cdist(lig_coords, lig_coords)

    src_list = []
    dst_list = []
    dist_list = []
    mean_norm_list = []
    for i in range(num_nodes):
        dst = list(np.where(distance[i, :] < radius)[0])
        dst.remove(i)
        if max_neighbors != None and len(dst) > max_neighbors:
            dst = list(np.argsort(distance[i, :]))[1: max_neighbors + 1]  # closest would be self loop
        if len(dst) == 0:
            dst = list(np.argsort(distance[i, :]))[1:2]  # closest would be the index i itself > self loop
            log(
                f'The lig_radius {radius} was too small for one lig atom such that it had no neighbors. So we connected {i} to the closest other lig atom {dst}')
        assert i not in dst
        assert dst != []
        src = [i] * len(dst)
        src_list.extend(src)
        dst_list.extend(dst)
        valid_dist = list(distance[i, dst])
        dist_list.extend(valid_dist)
        valid_dist_np = distance[i, dst]
        sigma = np.array([1., 2., 5., 10., 30.]).reshape((-1, 1))
        weights = softmax(- valid_dist_np.reshape((1, -1)) ** 2 / sigma, axis=1)  # (sigma_num, neigh_num)
        assert weights[0].sum() > 1 - 1e-2 and weights[0].sum() < 1.01
        diff_vecs = lig_coords[src, :] - lig_coords[dst, :]  # (neigh_num, 3)
        mean_vec = weights.dot(diff_vecs)  # (sigma_num, 3)
        denominator = weights.dot(np.linalg.norm(diff_vecs, axis=1))  # (sigma_num,)
        mean_vec_ratio_norm = np.linalg.norm(mean_vec, axis=1) / denominator  # (sigma_num,)

        mean_norm_list.append(mean_vec_ratio_norm)
    assert len(src_list) == len(dst_list)
    assert len(dist_list) == len(dst_list)
    graph = dgl.graph((torch.tensor(src_list), torch.tensor(dst_list)), num_nodes=num_nodes, idtype=torch.int32)

    graph.ndata['feat'] = lig_atom_featurizer(mol)
    graph.edata['feat'] = distance_featurizer(dist_list, 0.75)  # avg distance = 1.3 So divisor = (4/7)*1.3 = ~0.75
    graph.ndata['x'] = torch.from_numpy(np.array(true_lig_coords).astype(np.float32))
    graph.ndata['mu_r_norm'] = torch.from_numpy(np.array(mean_norm_list).astype(np.float32))
    if use_rdkit_coords:
        graph.ndata['new_x'] = torch.from_numpy(np.array(lig_coords).astype(np.float32))
    return graph

节点特征

def lig_atom_featurizer(mol):     # 在所有PDB结合中，它们是93个分子的Nan。我们在这种情况下打0。
    ComputeGasteigerCharges(mol)  # they are Nan for 93 molecules in all of PDBbind. We put a 0 in that case. 计算出的partial charge存储在每个原子的属性中
    ringinfo = mol.GetRingInfo()
    atom_features_list = []
    for idx, atom in enumerate(mol.GetAtoms()):
        g_charge = atom.GetDoubleProp('_GasteigerCharge') # 通过GetDoubleProp(浮点数)或GetProp(字符串)来获取。
        atom_features_list.append([
            safe_index(allowable_features['possible_atomic_num_list'], atom.GetAtomicNum()),
            allowable_features['possible_chirality_list'].index(str(atom.GetChiralTag())),
            safe_index(allowable_features['possible_degree_list'], atom.GetTotalDegree()),
            safe_index(allowable_features['possible_formal_charge_list'], atom.GetFormalCharge()),
            safe_index(allowable_features['possible_implicit_valence_list'], atom.GetImplicitValence()),
            safe_index(allowable_features['possible_numH_list'], atom.GetTotalNumHs()),
            safe_index(allowable_features['possible_number_radical_e_list'], atom.GetNumRadicalElectrons()),
            safe_index(allowable_features['possible_hybridization_list'], str(atom.GetHybridization())),
            allowable_features['possible_is_aromatic_list'].index(atom.GetIsAromatic()),
            safe_index(allowable_features['possible_numring_list'], ringinfo.NumAtomRings(idx)),
            allowable_features['possible_is_in_ring3_list'].index(ringinfo.IsAtomInRingOfSize(idx, 3)),
            allowable_features['possible_is_in_ring4_list'].index(ringinfo.IsAtomInRingOfSize(idx, 4)),
            allowable_features['possible_is_in_ring5_list'].index(ringinfo.IsAtomInRingOfSize(idx, 5)),
            allowable_features['possible_is_in_ring6_list'].index(ringinfo.IsAtomInRingOfSize(idx, 6)),
            allowable_features['possible_is_in_ring7_list'].index(ringinfo.IsAtomInRingOfSize(idx, 7)),
            allowable_features['possible_is_in_ring8_list'].index(ringinfo.IsAtomInRingOfSize(idx, 8)),
            g_charge if not np.isnan(g_charge) and not np.isinf(g_charge) else 0.
        ])

    return torch.tensor(atom_features_list)

配体原子几何图

首先遍历分子原子，这些原子最为源节点， 然后找到两条跳内的邻居节点作为目标节点，边特征来自于节点间几何距离。

def get_geometry_graph(lig):
    coords = lig.GetConformer().GetPositions()
    edges_src = []
    edges_dst = []
    for i, atom in enumerate(lig.GetAtoms()):
        src_idx = atom.GetIdx()
        assert src_idx == i
        one_hop_dsts = [neighbor for neighbor in list(atom.GetNeighbors())]
        two_and_one_hop_idx = [neighbor.GetIdx() for neighbor in one_hop_dsts]
        for one_hop_dst in one_hop_dsts:
            for two_hop_dst in one_hop_dst.GetNeighbors():
                two_and_one_hop_idx.append(two_hop_dst.GetIdx())
        all_dst_idx = list(set(two_and_one_hop_idx))
        if len(all_dst_idx) ==0: continue
        all_dst_idx.remove(src_idx)
        all_src_idx = [src_idx] *len(all_dst_idx)
        edges_src.extend(all_src_idx)
        edges_dst.extend(all_dst_idx)
    graph = dgl.graph((torch.tensor(edges_src), torch.tensor(edges_dst)), num_nodes=lig.GetNumAtoms(), idtype=torch.long)
    graph.edata['feat'] = torch.from_numpy(np.linalg.norm(coords[edges_src] - coords[edges_dst], axis=1).astype(np.float32))
    return graph

Equibind模型

模型输入

• 配体图：
  节点特征：原子相关化学特征、原子坐标（RDKIT重新生成）、Surface-aware node feature
  边特征：距离特征
• 受体图：
  节点特征：α-C原子坐标、surface-aware node feature、氨基酸名称位置索引，溶剂接触表面积，bfactor（晶体衍射因子）
  边特征：距离、相对位置、相对角度特征
• 配体几何图：
  边特征：距离（数据真实坐标计算得来）

网络层

IEGMN（等变图匹配网络）