进位
进位
加粗

最近想出了不适用运算符实现加与减

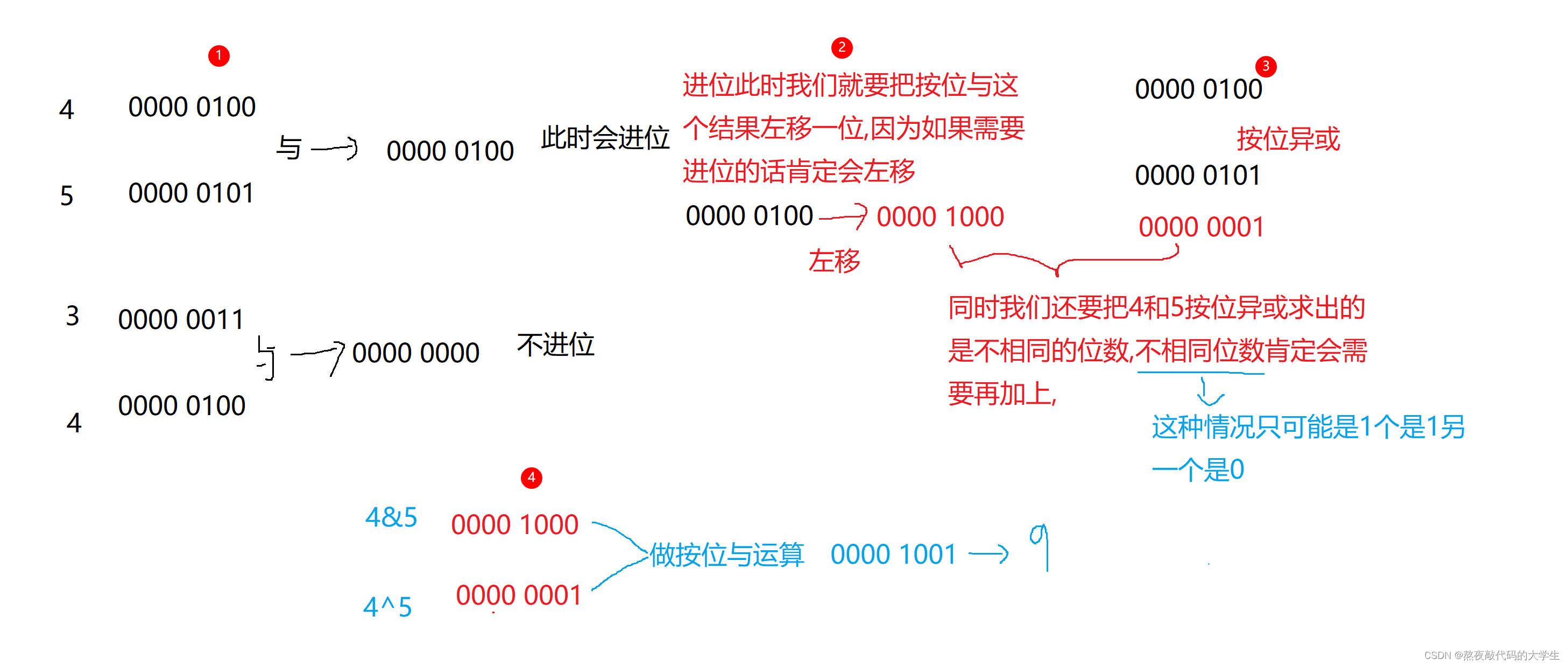
首先按位与找出的是需不需要进位

按位与是两边同时为1,则为1,那么如果两边同时为1的话,是不是就该进位?所以我们用按位与来判断是否需要进位

然后再按位异或找出不同的位数

按位异或是两边不相等,也就是1 和 0的时候才会1,那我如果在整数的二进制为中,一边是0,一边是1,我们是不是直接相加就可以了呢? 那么相加的结果就是1

最后按位或

按位或是两边只要有一个是1,就为1,那么我们是不是可以用这个来实现我们前面按位与和按位异或的结果相加呢?答案是可以的。

但是使用按位或的前提是按位与的结果和按位异或的结果,这两个再按位与的结果为0，才可以进行按位或,就和上面那个图一样。

4 – 0000 0100
5 – 0000 0101
4 & 5
0000 0100
不是0再左移一位
0000 1000

----------------------------------------------------分隔栏
4 – 0000 0100
5 – 0000 0101
4 ^ 5
0000 0001

(4 & 5) & (4 ^ 5) == 0
此时直接按位或
0000 1000
0000 0001
按位或
结果为0000 1001
只有当按位与和按位异或再按位与的结果为0的时候，才能按位或，不然的话还是有可以进位的,如果不这么继续整的话,就会算错
上图中4,5只是一次就搞定了,下面在举一个 15 和 25 的例子。

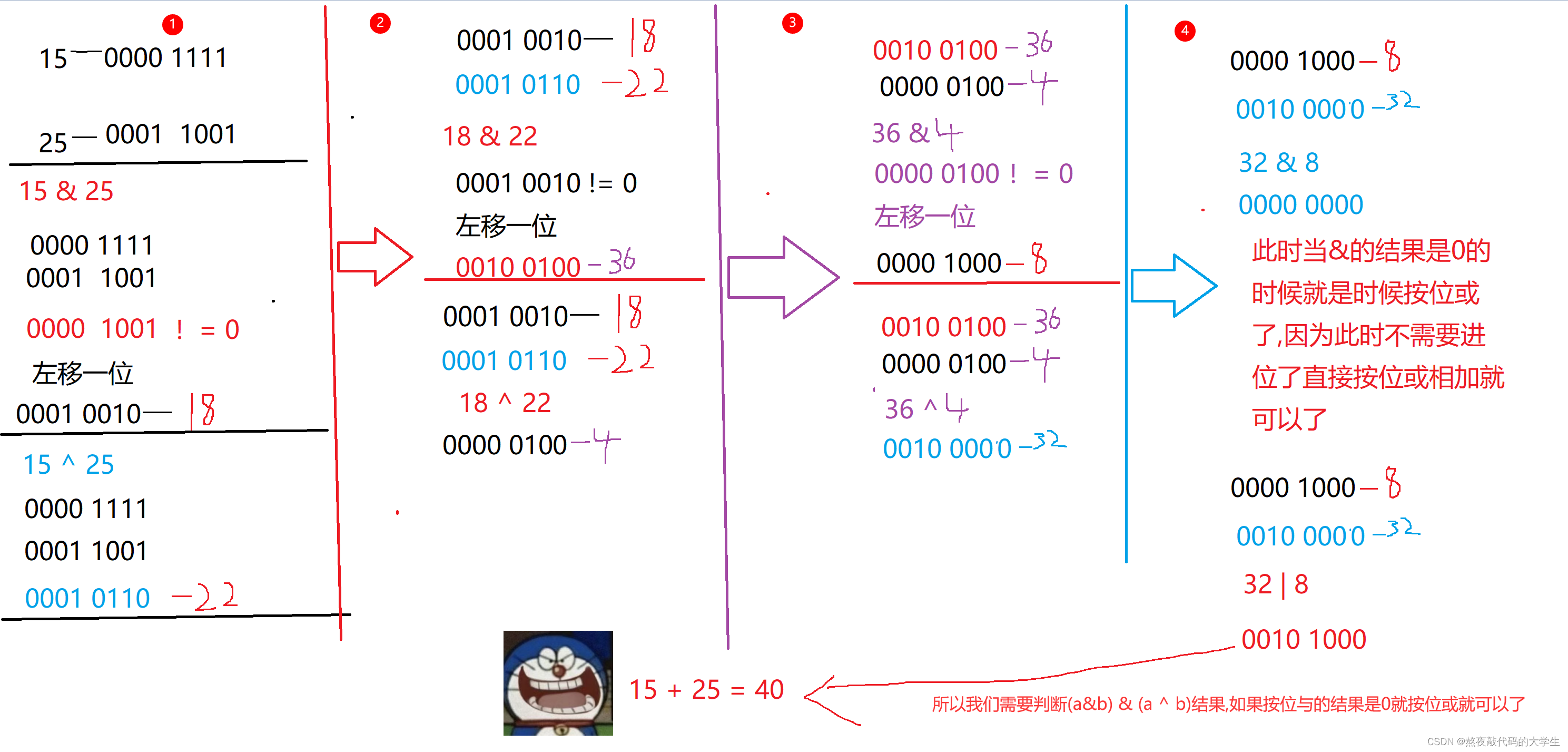
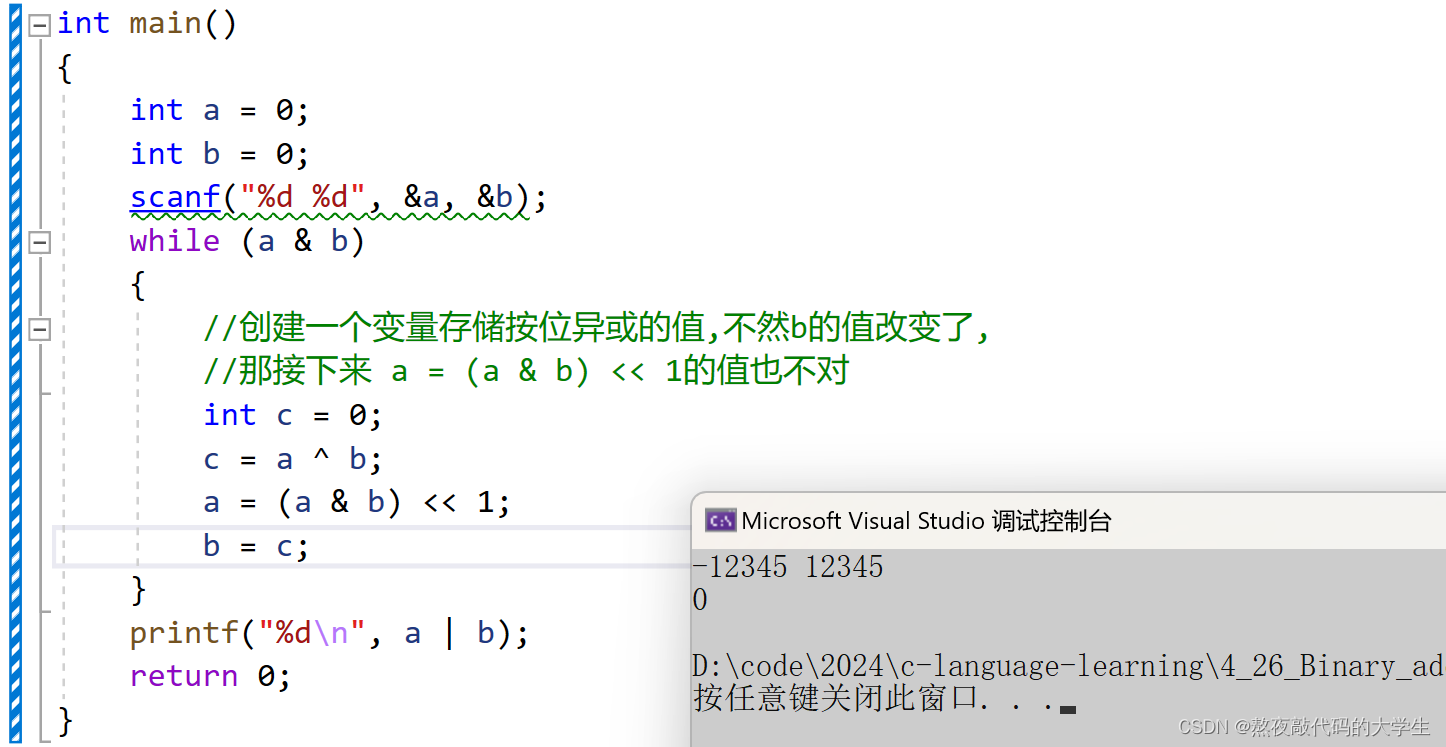
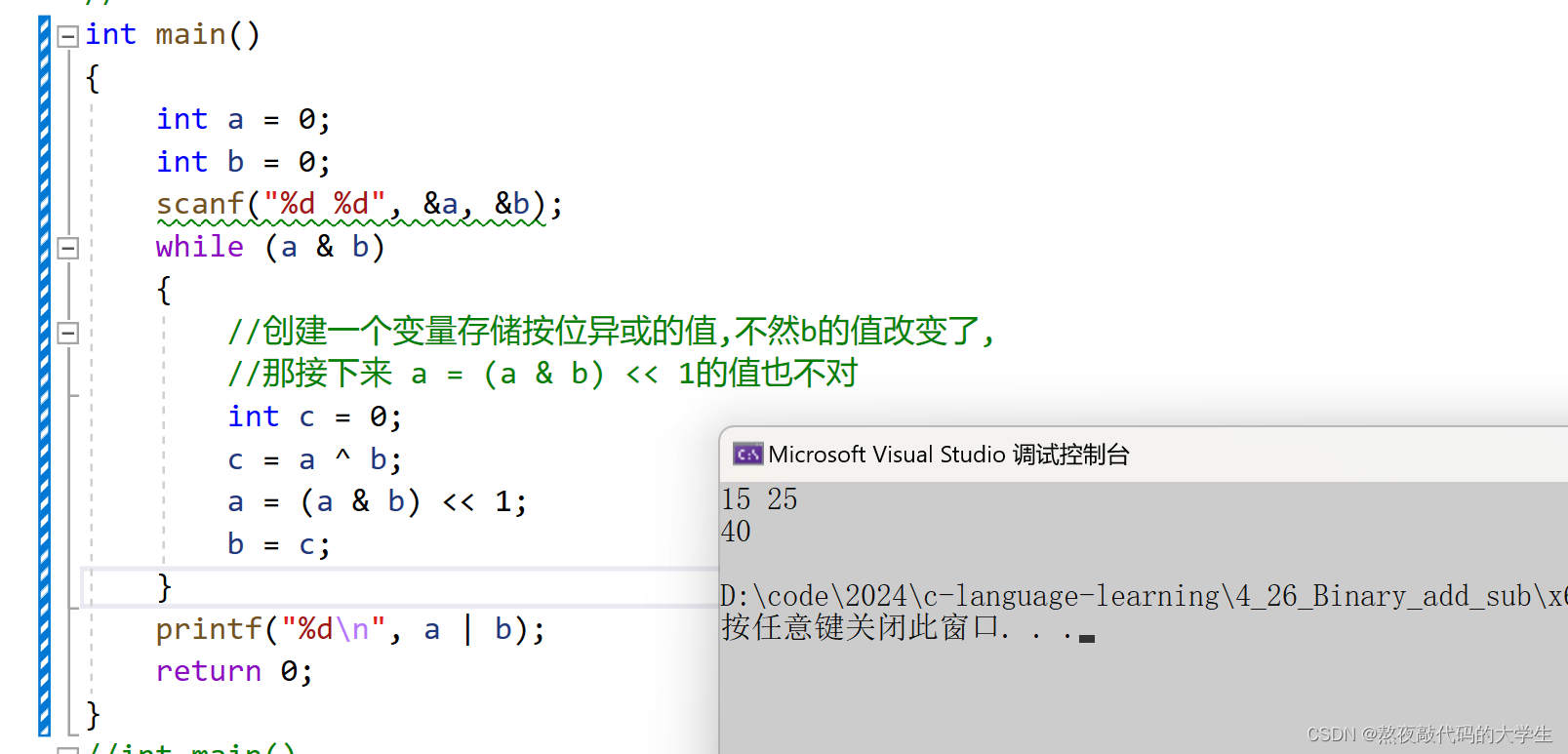
代码实现:

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	while (a & b)
	{
		//创建一个变量存储按位异或的值,不然b的值改变了,
		//那接下来 a = (a & b) << 1的值也不对 
		int c = 0;
		c = a ^ b;
		a = (a & b) << 1;
		b = c;
	}
	printf("%d\n", a | b);
	return 0;
}

减法也可以