LAPGAN
引言
在原始 GAN和CGAN中,还只能生成 16*16, 28*28, 32*32 这种低像素小尺寸的图片。而LAPGAN首次实现 64*64 的图像生成。与其一下子生成这么大的图像 (包含信息量这么多),不如一步步由小到大,这样每一步生成的时候,可以基于上一步的结果,而且还只需要“填充”和“补全”新图片所需要的那些信息。
LAPGAN的思想
LAPGAN通过级联方式改进GAN以实现从粗略到精细图片的生成。网络的级联思想对后续的研究产生了极大的影响。LAPGAN使用高斯金字塔进行下采样,使用拉普拉斯金字塔进行上采样
假设图像 I I I的长度和宽度均为 j j j,对于图像 I 0 = ( j , j ) I_0=(j,j) I0=(j,j),下采样得到的图像尺寸为( j / 2 , j / 2 ) j/2,j/2) j/2,j/2),上采样得到的图像尺寸为(2 j j j,2 j j j)。对于图像进行连续 k k k 次的下采样,可以获得一系列图像 I 1 = ( j / 2 , j / 2 ) , I 2 = ( j / 4 , j / 4 ) , . . . , I k = I_1=(j/2,j/2),I_2=(j/4,j/4),...,I_k= I1=(j/2,j/2),I2=(j/4,j/4),...,Ik= ( j / 2 k , j / 2 k ) : (j/2^k,j/2^k): (j/2k,j/2k):
其中, g ( I ) g(I) g(I)表示图像的高斯金字塔。在得到高斯金字塔之后,拉普拉斯金字塔可表示如下:
h
k
=
L
k
(
I
)
=
G
k
(
I
)
−
u
(
G
k
+
1
(
I
)
)
=
I
k
−
u
(
I
k
+
1
)
\boldsymbol{h}_k=\mathcal{L}_k(\boldsymbol{I})=\mathcal{G}_k(\boldsymbol{I})-u\big(\mathcal{G}_{k+1}(\boldsymbol{I})\big)=\boldsymbol{I}_k-u(\boldsymbol{I}_{k+1})
hk=Lk(I)=Gk(I)−u(Gk+1(I))=Ik−u(Ik+1)
其中,拉普拉斯金字塔的第
k
k
k层等于高斯金字塔的第
k
k
k层
g
k
(
I
)
g_k(I)
gk(I)减去高斯金字塔第(k+1)层的上采样
u
(
g
k
+
1
(
I
)
)
u(g_{k+1}(I))
u(gk+1(I))
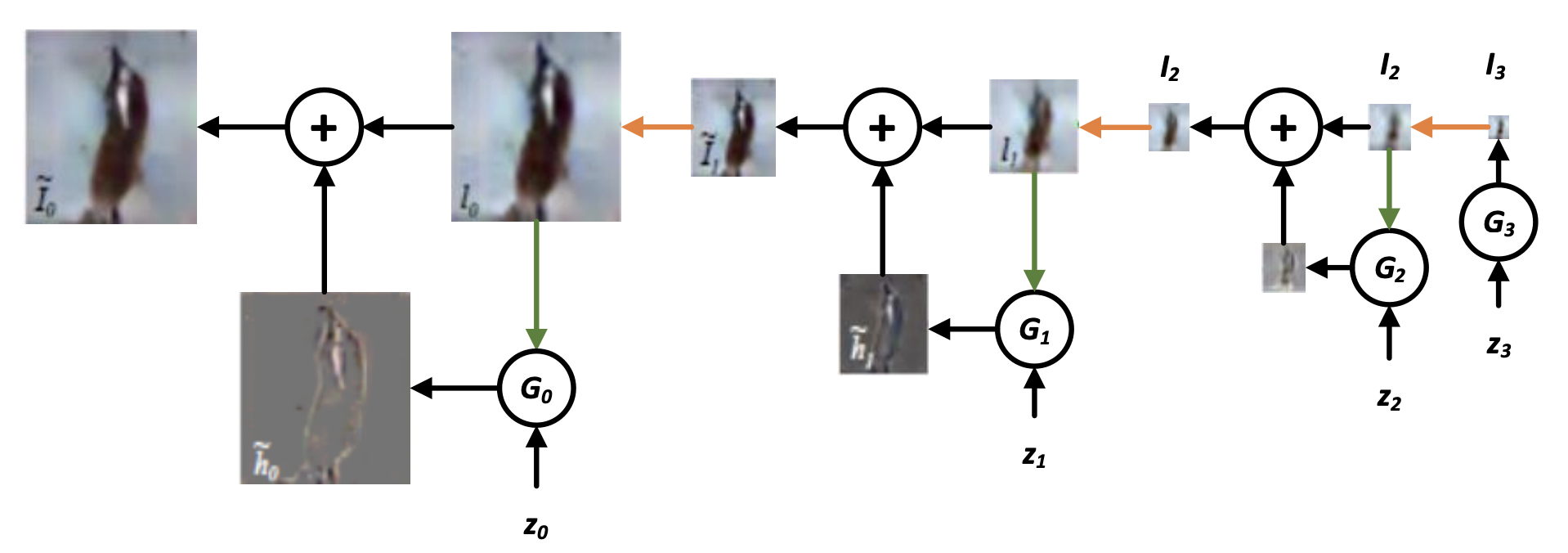
输入噪声z 3 ′ _{3^{\prime}} 3′ 经 G 3 G_{3} G3生成 I ~ 3 \tilde{I}_{3} I~3,上采样得到 I 2 I_{2} I2,使用 I 2 I_{2} I2作为条件输入 G 2 , G_{2,} G2, 同时输入噪声z 2 _{2} 2生成差分图像 h ~ 2 \tilde{h}_{2} h~2, 添加到 I 2 I_{2} I2中生成 I ~ 2 \tilde{I}_{2} I~2。
LAPGAN将条件对抗生成网络CGAN集成到拉普拉斯金字塔结构中:
I
~
k
=
u
(
I
~
k
+
1
)
+
h
~
k
=
u
(
I
~
k
+
1
)
+
G
k
(
z
k
,
u
(
I
~
k
+
1
)
)
\tilde{\boldsymbol{I}}_k=u(\tilde{\boldsymbol{I}}_{k+1})+\tilde{\boldsymbol{h}}_k=u(\tilde{\boldsymbol{I}}_{k+1})+G_k(\mathbf{z}_k,u(\tilde{\boldsymbol{I}}_{k+1}))
I~k=u(I~k+1)+h~k=u(I~k+1)+Gk(zk,u(I~k+1))
其中,
G
k
G_k
Gk表示第
k
k
k个卷积神经网络,也就是生成器,高斯金字塔第
k
k
k层的重建等于它的第
(
k
+
1
)
(k+1)
(k+1)层上采样
u
(
I
~
k
+
1
)
u(\tilde{I}_{k+1})
u(I~k+1)加上拉普拉斯金字塔的第
k
k
k层
h
~
k
\widetilde{h}_k
h
k。除了最高层的生成器之外,其余生成器
G
0
G_0
G0、
G
1
…
G
k
−
1
G_1\ldots G_{k-1}
G1…Gk−1都是采用上一级的上采样和噪声作为联合输入。上采样的结果就是LAPGAN中的条件变量。
Coarse-to-fine的视觉效果