一、说明

有些函数系列极具线性代数的向量特征。这里谈及多项式构成函数的线性代数意义。问题是这个主题能展开多少内涵？请看本文的论述。

二、线性空间和向量

让我先问你一个简单的问题。什么是向量？为了方便起见，二维箭头从根本上说是平面上的箭头吗？或者从根本上说，是那对实数，恰好在平面上可视化为箭头？或者这两种表现都是更深层次的东西？

一方面，将向量定义为一个数字列表是如此清晰，缺乏更深层次的含义。它使 4 维向量和 100 维向量听起来像是您可以使用的真实具体想法，而实际上，像 4 维这样的想法是可以挥动的模糊几何概念。

此外，在线性代数中，您正在使用一个独立于您赋予它的坐标的空间。坐标实际上有些随意，具体取决于您选择的基础向量。线性代数中的核心主题，如行列式和特征向量，似乎与你选择的坐标系无关。

行列式告诉您变换对面积的缩放程度，特征向量是在变换期间保持在其自身跨度上的向量。但这两个属性本质上都是空间性的。您可以自由更改坐标系，而无需更改任何一个的基础值。

如果向量从根本上说不是实数列表，如果潜在的本质是更空间的东西，那么就会带来一个问题，即空间这个词的真正含义是什么？

为了建立这一点，让我们谈谈不是数字或箭头但具有向量性质的东西。功能！

从某种意义上说，函数是另一种类型的向量。以同样的方式，您可以将两个向量相加，也可以对函数执行相同的操作。让我们以函数 f 和 g 为例。例如，当您取两个函数的总和并在 -4 处计算时，它是 f 和 9 的输出之和，当您在 -4 处计算它们时。这类似于逐个坐标添加向量，但从某种意义上说，有无限多的坐标需要处理。

还有一个明智的概念是用实数缩放函数。您所要做的就是按该数字缩放所有输出。这类似于逐个坐标缩放向量。感觉就像有无限多的坐标。

向量唯一能做的就是相加或缩放，感觉我们应该能够采用最初在空间中考虑的相同有用的结构（线性变换、零空间、点积、特征-一切）和代数问题解决技术，并将它们应用于函数。

例如，函数的线性变换有一个完全合理的概念。接受一个功能并将其转换为另一个功能的东西。我想到的一个例子是导数。它将一个函数转换为另一个函数。它们也称为线性算子。

但是，函数的线性变换意味着什么呢？如果变换可以满足两个属性，即可加性和缩放性，则变换是线性的。可加性意味着，如果将两个向量 v 和 w 相加，然后对它们的总和进行变换，则得到的结果与将 v 和 w 的变换版本相加的结果相同。

缩放属性是当您将向量 v 缩放某个数字，然后应用变换时，您将获得与将 v 的变换版本缩放相同的最终向量。这通常被描述为线性变换保留了向量加法和标量乘法。

网格线保持平行且均匀分布的想法实际上说明了这两个属性在 2D 空间中点的特定情况下的含义。

这些属性使矩阵向量乘法成为可能的最重要结果之一是线性变换完全由它采用基向量的位置来描述。由于任何向量都可以通过缩放和添加基向量来表示，因此查找向量的变换版本归结为以相同的方式缩放和添加基向量的变换版本。对于函数和箭头来说都是如此。

例如，在微积分中，我们总是使用导数是可加的并且具有缩放属性这一事实，即使它没有这样表述。如果将两个函数相加，然后取导数，则与先取这些函数的导数并将它们相加是一样的。同样，如果你缩放一个函数，取导数，这与先取导数然后缩放函数是一样的。

为了更深入地理解这一点，让我们看看用矩阵表示导数会是什么样子。让我们将空间限制为多项式。我们空间中的每个多项式都有有限个项，但整个空间包括任意大次的多项式。我们需要做的第一件事是选择一个基础。由于多项式已经写成变量 x 的缩放幂之和，因此选择 x 的幂作为基函数是有意义的。

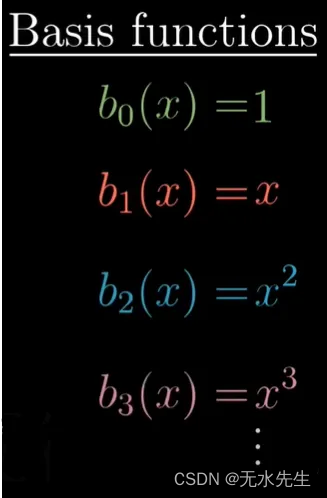
源 https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16

三、向量的内积

这些基本函数的作用类似于 i-hat、j-hat 和 k-hat 在向量世界中的角色。由于我们的多项式可以具有任意大的度数，因此基函数的集合是无限的。这意味着当我们将多项式视为向量时，它们将具有无限多个坐标。

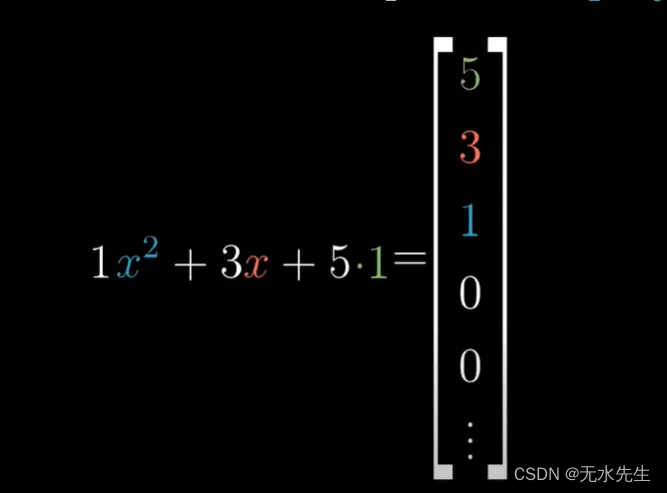
源 https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16
你读到这句话时说它的 5 倍于第一个基函数加上 3 倍的第二个加 1 倍于第三个基函数，并且在此之后不应添加任何其他基函数。

源 https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16
由于每个多项式都有微弱的多项，因此它的坐标将是一些有限的数字字符串，其无限尾部为 0。在这个坐标系中，导数用一个无限矩阵来描述，该矩阵大多充满 0，但正整数在偏移对角线上倒计时。

源 https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16

四、多项式的矩阵表达

取代表多项式的坐标：x³ + 5x² + 4x + 5。现在把这些坐标放在上面矩阵的右边。唯一有助于结果第一个坐标的项是 1 * 4。这意味着结果中的常数项将为 4。这对应于 4x 的导数为 4 的事实。唯一有助于矩阵第二坐标的项是 2 乘以 5。这意味着导数中 x 的系数 Infront 为 10，对应于 5x² 的导数。类似地，矩阵向量乘积中的 3 坐标归结为 takin 3 * 1。这个对应于 x³ 的导数为 3x²。在那之后，它只会是 0s。使这成为可能的原因是导数是线性的。

可以通过取每个基函数的导数并将结果的坐标放在每列中来构造此矩阵。令人惊讶的是，矩阵向量乘法和取导数乍一看似乎是完全不同的想法，但实际上都是该系列的相同成员。诸如线性变换、点积和特征向量之类的东西，我们认为只适用于线性代数概念，也适用于函数（只是名称可能不同）。

来源 — https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16
现在让我们回到什么是向量的问题！所有这一切的重点是指出数学中有很多向量的东西。只要您正在处理一组对象，其中有一个合理的缩放和添加概念。

想象一下，你正在发展线性代数理论，你希望所有的定义和发现都完全普遍地应用于所有向量类事物。这些向量类的东西集被称为向量空间，您可以在其中建立一组向量加法和缩放必须遵循的规则。这些规则被称为公理，在现代线性代数理论中有 8 条。

source — 来源 — https://www.youtube.com/watch?v=TgKwz5Ikpc8&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=16
公理本身并不是自然界的基本规则，而是一个人和其他人之间的接口，他们希望将这些结果应用于新的向量空间。

假设有人定义了一个新的向量空间，那么这些公理就像一个检查清单，他们需要验证这些定义，然后才能开始应用线性代数的结果。因此，人们必须只根据这些公理抽象地构建结果。

这就是为什么每本教科书都使用可加性和缩放来定义线性变换，而不是谈论保持平行和均匀间隔的网格线。因此，什么是向量这个问题的答案是，实际上它们所采用的形式并不重要！