介绍

有些人发现很难理解递归算法。

这个技巧向绝对初学者展示了如何使用递归查找排列。Python

背景

这个技巧的想法来自一个问答问题：可怜的 OP 花了三天时间“翻头”，试图弄清楚一小段代码如何能够生成输入列表项的所有排列。为了阻止这种危险的运动，我试图阐明这一论点。Python

1. 问题

问题是：找到一个集合的所有排列。粗略地说，我们必须找到集合元素的所有不同排列。

2. “纸和铅笔”方法

让我们从简单开始。考虑一个具有单个元素的集合。显然，这个可怜的、孤独的物品的唯一安排就是它自己。1

2.1 {1}的排列

<span style="color:#111111"><span style="background-color:#ffffff"><span style="color:#000000"><span style="background-color:#fbedbb">P[1]  =  1</span></span></span></span>

现在考虑两个元素，所有的排列都简化为一个简单的交换。

2.2 {1,2}的排列

<span style="color:#111111"><span style="background-color:#ffffff"><span style="color:#000000"><span style="background-color:#fbedbb">           1 2
P[1 2]  =
           2 1</span></span></span></span>

最后，考虑三个要素：稍加努力，我们写：

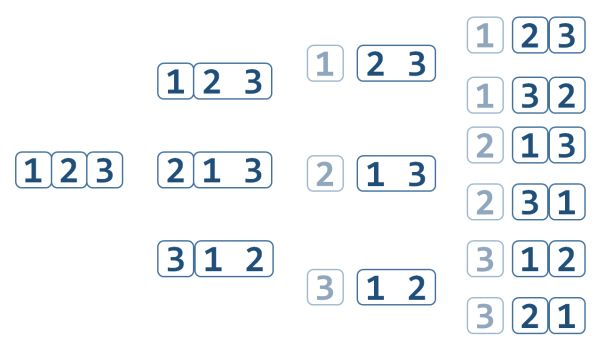
2.3 {1,2,3}的排列

<span style="color:#111111"><span style="background-color:#ffffff"><span style="color:#000000"><span style="background-color:#fbedbb">             1 2 3
		   
             1 3 2
		   
             2 1 3
P[1 2 3]  =           
             2 3 1
		   
             3 1 2
		   
             3 2 1</span></span></span></span>

3. 新兴模式

考虑最后一个示例，有一个新兴模式：首先，我们选择了集合的第一个元素（即 ）。{1,2,3}1

然后，对于剩余的项目（即 和 ），我们按照配方继续，也就是说，我们已经交换了它们。232.2

最后，我们分别选择了第二项和第三项，并对其余项进行了类似的操作。

总结一下：