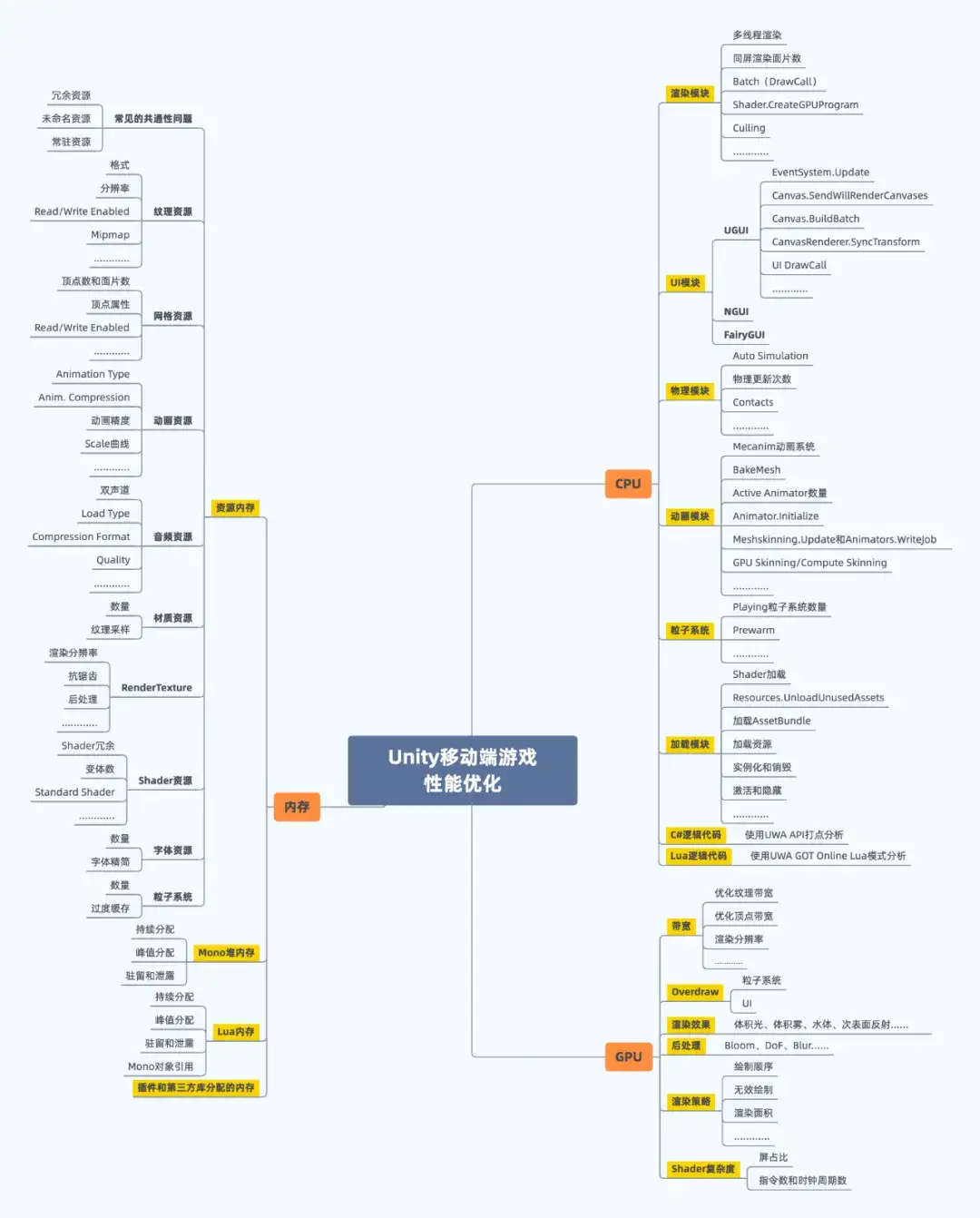
(文章的主要内容来自电科的顾亦奇老师的 Mathematical Foundation of Deep Learning, 有部分个人理解)
一般深度神经网络的微分
上周讨论的前向和反向传播算法可以推广到任意深度神经网络的微分。
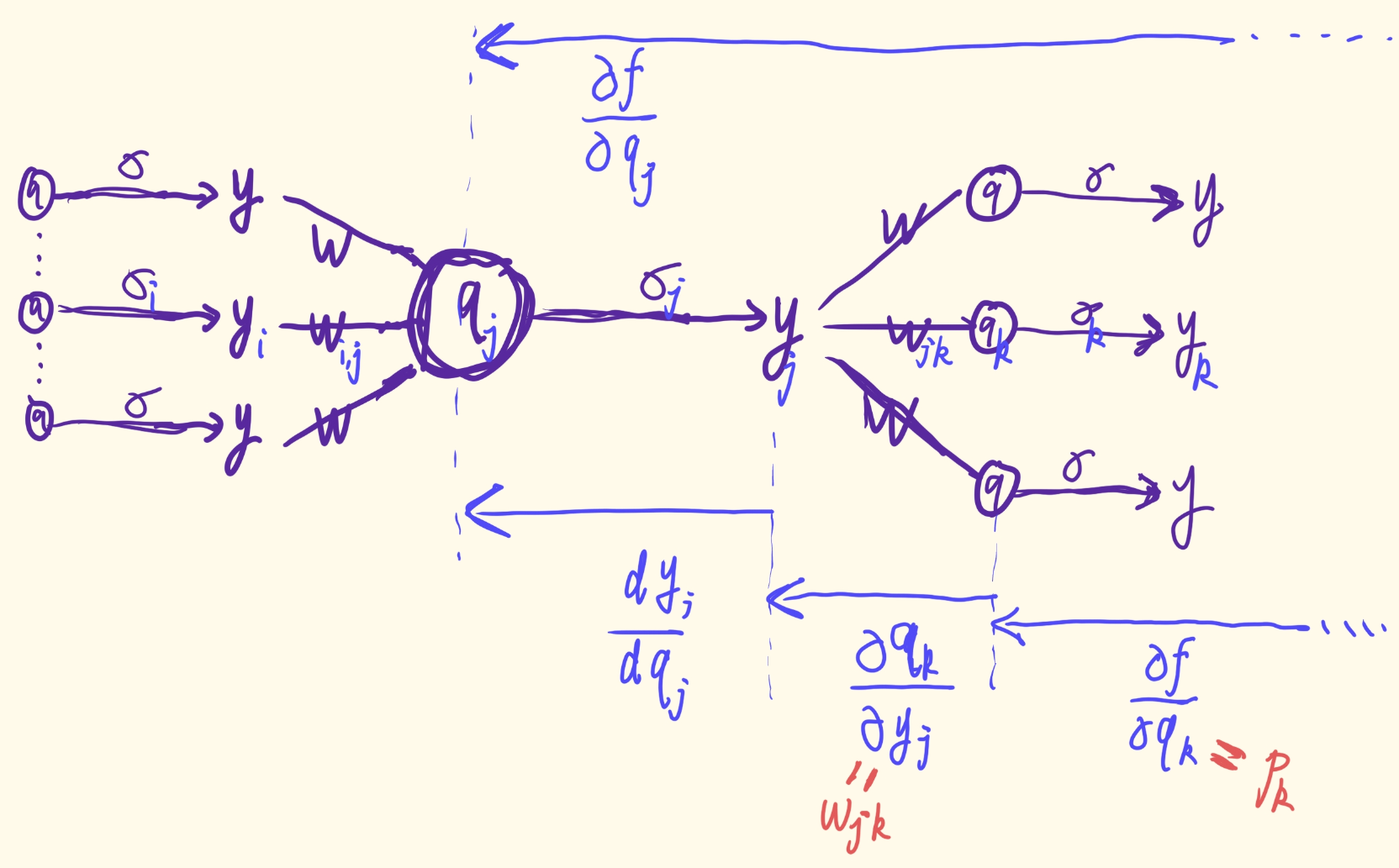
对于一般的网络来说,可能无法逐层分割,但仍然可以用流图来表示。因此,反向传播是通过从输出神经元开始、向后传递信息并在输入处结束来执行的。
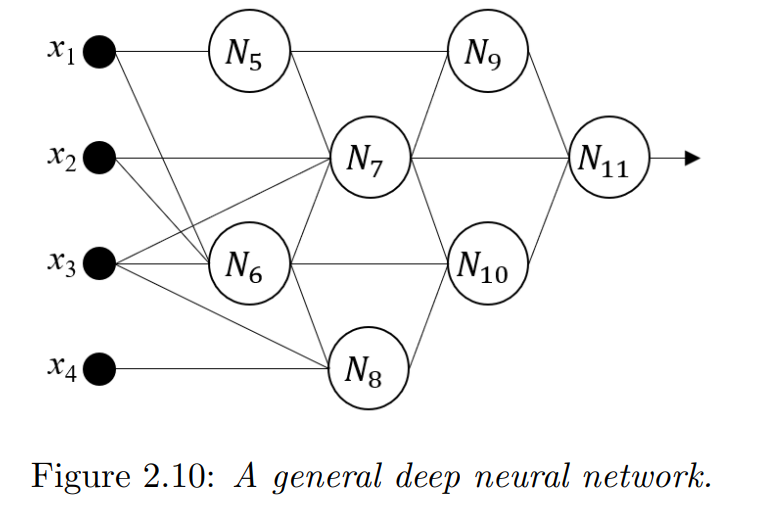
更准确地说,给定从 R d \mathbb{R}^{d} Rd到 R \mathbb{R} R的神经网络 f ( x ; θ ) f(x; θ) f(x;θ) 映射图,假设总共有 K 个神经元,我们用 x 1 , … , x d x_1, \dots ,x_d x1,…,xd和 N d + 1 , … , N d + K N_{d+1}, \dots ,N_{d+K} Nd+1,…,Nd+K标记输入。为了方便起见,神经元被标记为使得有向边总是从小索引到大索引。
我们用
w
i
,
j
w_{i,j}
wi,j 表示从神经元
N
i
N_i
Ni(或输入
x
i
x_i
xi)到神经元
N
j
N_j
Nj 的边的权重。 令
P
j
P_j
Pj 为由神经元
N
j
N_j
Nj 的直接前驱的索引组成的集合
(
d
+
1
≤
j
≤
d
+
K
)
(d + 1 ≤ j ≤ d + K)
(d+1≤j≤d+K)。 类似地,令
S
j
S_j
Sj 为由顶点
x
j
x_j
xj 或
N
j
N_j
Nj 的直接后继索引组成的集合
(
1
≤
j
<
d
+
K
)
(1 ≤ j < d + K)
(1≤j<d+K)。 例如,在图 2.10 中,
P
7
=
{
2
,
3
,
5
,
6
}
P_7 = \{2,3,5,6\}
P7={2,3,5,6},
S
7
=
{
9
,
10
,
11
}
S_7 = \{9,10,11\}
S7={9,10,11}。
现在,对于任何
1
≤
j
≤
d
+
K
1 ≤ j ≤ d + K
1≤j≤d+K,假设以下计算发生在
N
j
N_j
Nj:
y
j
=
σ
j
(
q
j
)
,
q
j
=
∑
k
∈
P
j
w
k
,
j
y
k
+
b
j
,
for
d
+
1
≤
j
≤
d
+
K
.
(2.27)
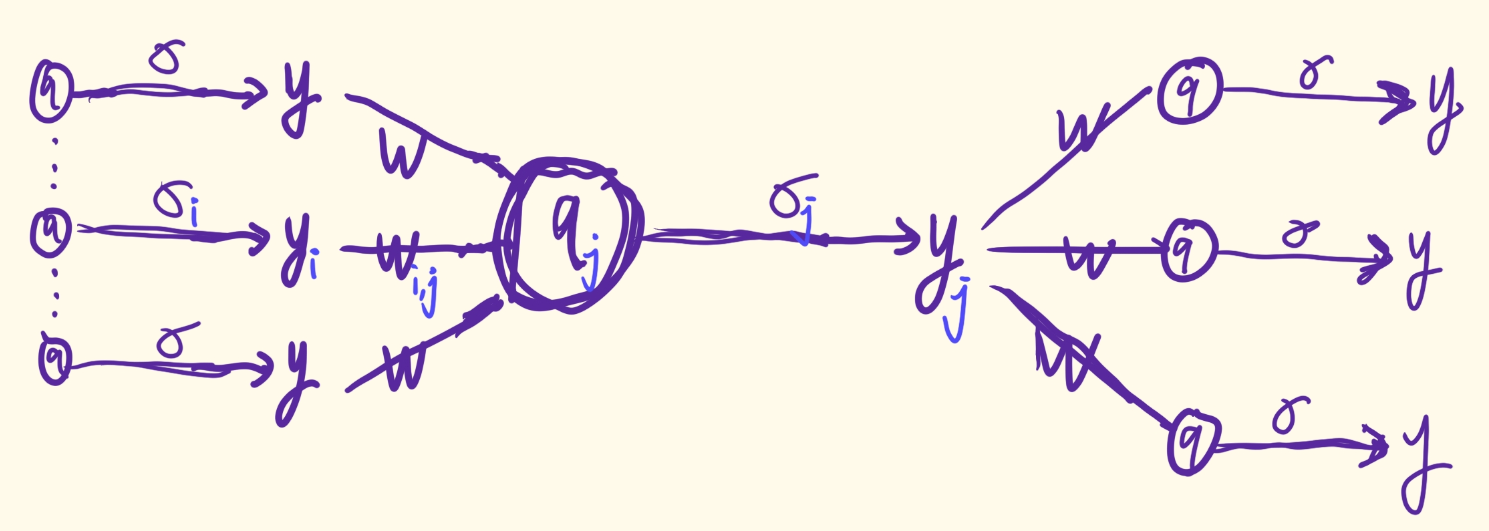
y _ { j } = \sigma _ { j } ( q _ { j } ) , \text{ } \text{ } q _ { j } = \sum _ { k \in P _ { j } } w _ { k , j } y _ { k } + b _ { j } , \text{for }\text{ } d + 1 \leq j \leq d + K . \tag{2.27}
yj=σj(qj), qj=k∈Pj∑wk,jyk+bj,for d+1≤j≤d+K.(2.27)
y
j
=
x
j
,
for
1
≤
j
≤
d
.
(2.28)
y _ { j } = x _ { j } , \text{ }\text{ }\text{for }\text{ } 1 \leq j \leq d . \tag{2.28}
yj=xj, for 1≤j≤d.(2.28)
其中
σ
j
σ_j
σj 和
b
j
b_j
bj 是
N
j
N_j
Nj 的激活函数和偏差。
恒等式(2.28)仅仅是为了符号方便。
请注意,
y
j
y_j
yj 表示顶点
N
j
N_j
Nj 或
x
j
x_j
xj 的输出值。
我们可以使用一种流程图来表示这个过程:
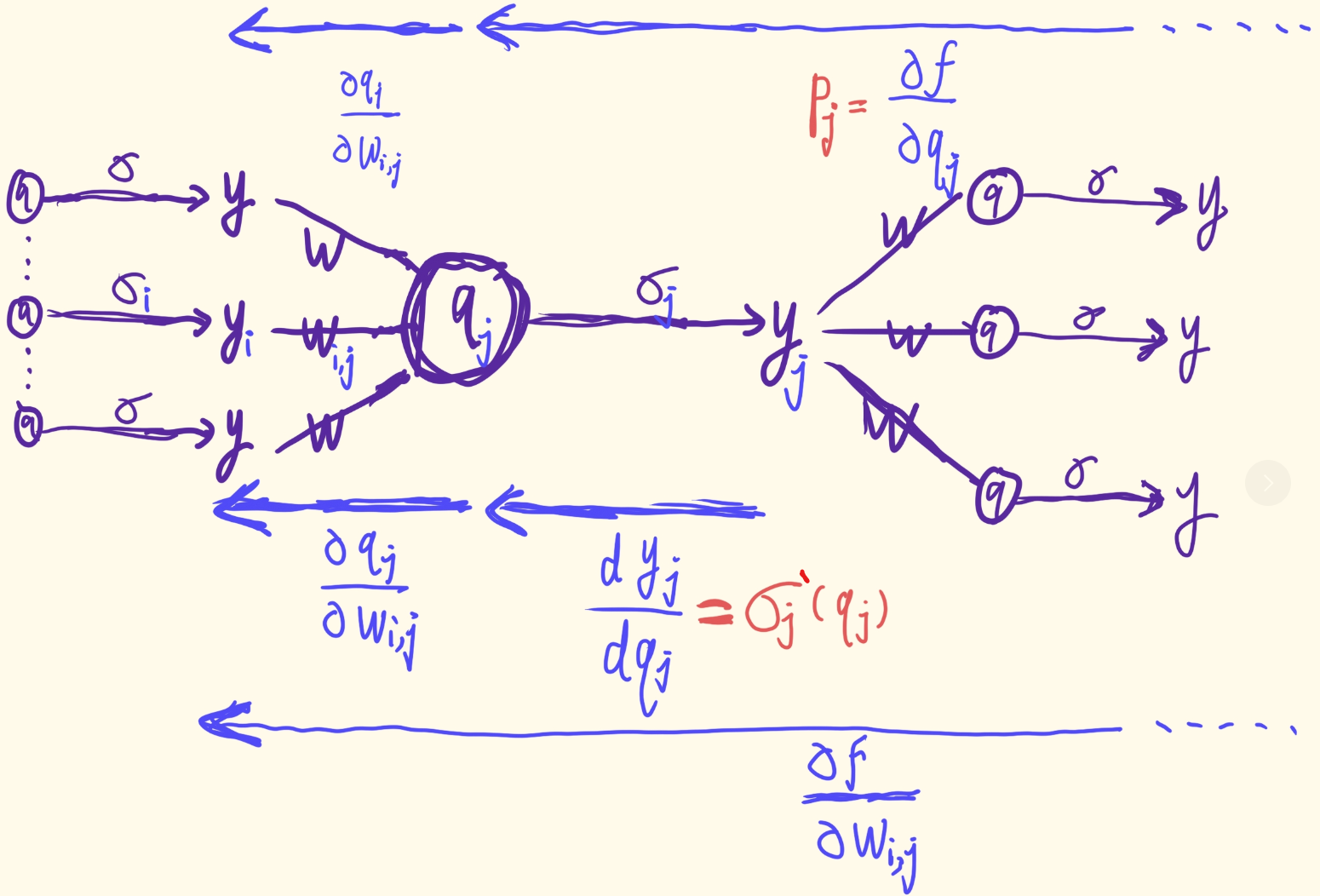
另外,我们将
p
j
p _ { j }
pj表示为
∂
f
(
x
;
θ
)
∂
q
j
\frac { \partial f ( x ; \theta ) } { \partial q _ { j } }
∂qj∂f(x;θ) 表示为
d
+
1
≤
j
≤
d
+
K
d + 1 ≤ j ≤ d + K
d+1≤j≤d+K.
使用链式法则,如果
i
∈
S
j
i ∈ S_j
i∈Sj ,我们有 (对于节点
N
j
N_j
Nj, f对其任意一个入度边
w
i
,
j
w_{i,j}
wi,j偏导表示) (这里
y
i
y_i
yi表示某个前导节点)
∂
f
(
x
;
θ
)
∂
w
i
,
j
=
∂
f
(
x
;
θ
)
∂
q
j
⋅
∂
q
j
∂
w
i
,
j
=
p
j
⋅
y
i
⋅
(2.29)
\frac { \partial f ( x ; \theta ) } { \partial w _ { i , j } } = \frac { \partial f ( x ; \theta ) } { \partial q _ { j } } \cdot \frac { \partial q _ { j } } { \partial w _ { i , j } } = p _ { j } \cdot y _ { i \cdot } \tag{2.29}
∂wi,j∂f(x;θ)=∂qj∂f(x;θ)⋅∂wi,j∂qj=pj⋅yi⋅(2.29)
∂
f
(
x
;
θ
)
∂
b
j
=
∂
f
(
x
;
θ
)
∂
q
j
⋅
∂
q
j
∂
b
j
=
p
j
.
(2.30)
\frac { \partial f ( x ; \theta ) } { \partial b _ { j } } = \frac { \partial f ( x ; \theta ) } { \partial q _ { j } } \cdot \frac { \partial q _ { j } } { \partial b _ { j } } = p _ { j } . \tag{2.30}
∂bj∂f(x;θ)=∂qj∂f(x;θ)⋅∂bj∂qj=pj.(2.30)
另外,
p
j
p_j
pj也可通过
p
j
=
∂
f
(
x
;
θ
)
∂
q
j
=
∑
k
∈
S
j
∂
f
(
x
;
θ
)
∂
q
k
⋅
∂
q
k
∂
y
j
⋅
d
y
j
d
q
j
=
σ
j
′
(
q
j
)
⋅
∑
k
∈
S
j
p
k
⋅
w
j
,
k
for
d
+
1
≤
j
<
d
+
K
.
(2.32)
p _ { j } = \frac { \partial f ( x ; \theta ) } { \partial q _ { j } } = \sum _ { k \in S _ { j } } \frac { \partial f ( x ; \theta ) } { \partial q _ { k } } \cdot \frac { \partial q _ { k } } { \partial y _ { j } } \cdot \frac { d y _ { j } } { d q _ { j } } \\ = \sigma _ { j } ^ { \prime } ( q _ { j } ) \cdot \sum _ { k \in S _ { j } } p _ { k } \cdot w _ { j , k } \text{ }\text{ }\text{ }\text{for }\text{ } d + 1 \leq j < d + K .\tag{2.32}
pj=∂qj∂f(x;θ)=k∈Sj∑∂qk∂f(x;θ)⋅∂yj∂qk⋅dqjdyj=σj′(qj)⋅k∈Sj∑pk⋅wj,k for d+1≤j<d+K.(2.32)来计算.
同时, 我们有
∂
f
(
x
;
θ
)
∂
x
j
=
∑
k
∈
S
j
∂
f
(
x
;
θ
)
∂
q
k
⋅
∂
q
k
∂
y
j
⋅
∂
y
j
∂
x
j
(2.33)
\frac { \partial f ( x ; \theta ) } { \partial x _ { j } } = \sum _ { k \in S _ { j } } \frac { \partial f ( x ; \theta ) } { \partial q _ { k } } \cdot \frac { \partial q _ { k } } { \partial y _ { j } } \cdot \frac { \partial y _ { j } } { \partial x _ { j } }\tag{2.33}
∂xj∂f(x;θ)=k∈Sj∑∂qk∂f(x;θ)⋅∂yj∂qk⋅∂xj∂yj(2.33)
因此,我们可以首先实现前向传播 (2.27)-(2.28),它传递来自输入
x
1
,
…
,
x
d
x_1, \dots, x_d
x1,…,xd 的信息到输出神经元
N
d
+
K
N_{d+K}
Nd+K
在此阶段,我们从小到大地计算并保存
j
=
1
,
…
,
d
+
K
j = 1,\dots, d+K
j=1,…,d+K 时的
{
y
j
}
\{y_j\}
{yj} 和
{
q
j
}
\{q_j\}
{qj}。
接下来,我们实现反向传播 (2.29)-(2.32),它从
N
d
+
K
N_{d+K}
Nd+K 传递到输入。 具体来说,我们依照
j
=
d
+
K
,
d
+
K
−
1
,
…
,
d
+
1
j = d+K, d+K-1,\dots, d+1
j=d+K,d+K−1,…,d+1计算
{
p
j
}
\{p_j\}
{pj}、
{
∂
f
(
x
;
θ
)
∂
w
i
,
j
}
i
∈
P
j
\left\{ \frac { \partial f ( x ; \theta ) } { \partial w _ { i , j} } \right\} _ { i \in P j }
{∂wi,j∂f(x;θ)}i∈Pj和
{
∂
f
(
x
;
θ
)
∂
b
j
}
\left\{ \frac { \partial f ( x ; \theta ) } { \partial b_j} \right\}
{∂bj∂f(x;θ)}. 最终,
j
=
1
,
…
,
d
j = 1,\dots, d
j=1,…,d时的
{
∂
f
(
x
;
θ
)
∂
x
j
}
\left\{ \frac { \partial f ( x ; \theta ) } { \partial x_j} \right\}
{∂xj∂f(x;θ)}可被公式(2.33)计算
由路径制定的导数
更一般地,我们可以制定导数的封闭形式。
在图论意义上,将
P
(
j
,
n
1
,
n
2
,
…
,
n
k
,
d
+
K
)
\mathcal{P}(j, n_1, n_2, \dots, n_k, d + K)
P(j,n1,n2,…,nk,d+K) 表示为从顶点
N
j
N_j
Nj 或
x
j
x_j
xj 通过神经元
N
n
1
,
N
n
2
,
…
,
N
n
k
N_{n_1}, N_{n_2}, \dots, N_{n_k}
Nn1,Nn2,…,Nnk 到输出神经元
N
d
+
K
N_{d+K}
Nd+K的路径。
然后根据链式法则,对于任何
d
+
1
≤
j
≤
d
+
K
d + 1 ≤ j ≤ d + K
d+1≤j≤d+K 且
i
∈
P
j
i ∈ P_j
i∈Pj,有
∂
f
(
x
;
θ
)
∂
w
i
,
j
=
y
i
⋅
∑
P
(
j
,
n
1
,
n
2
,
…
,
n
k
,
d
+
K
)
σ
j
′
(
q
j
)
⋅
w
j
,
n
1
⋅
σ
n
1
′
(
q
n
1
)
⋅
w
n
1
,
n
2
⋅
σ
n
2
′
(
q
n
2
)
⋯
w
n
k
,
d
+
K
⋅
σ
d
+
K
′
(
q
d
+
K
)
,
(2.34)
\frac { \partial f ( x ; \theta ) } { \partial w _ { i , j } } = y _ { i } \cdot \sum _ { \mathcal{P} ( j , n _ { 1 } , n _ { 2 } , \ldots , n _ { k } , d + K ) } \sigma _ { j } ^ { \prime } ( q _ { j } ) \cdot w _ { j , n _ { 1 } } \cdot \sigma _ { n _ { 1 } } ^ { \prime } ( q _ { n _ { 1 } } ) \cdot w _ { n _ { 1 } , n _ { 2 } } \cdot \sigma _ { n _ { 2 } } ^ { \prime } ( q _ { n _ { 2 } } ) \cdots w _ { n _ { k }, d+K } \cdot \sigma _ { d + K } ^ { \prime } ( q _ { d + K } ) ,\tag{2.34}
∂wi,j∂f(x;θ)=yi⋅P(j,n1,n2,…,nk,d+K)∑σj′(qj)⋅wj,n1⋅σn1′(qn1)⋅wn1,n2⋅σn2′(qn2)⋯wnk,d+K⋅σd+K′(qd+K),(2.34)其中对从节点
N
j
N_j
Nj 到
N
d
+
K
N_{d+K}
Nd+K 的所有路径进行求和。 类似地,对于
1
≤
j
≤
d
1 ≤ j ≤ d
1≤j≤d,有:
∂
f
(
x
;
θ
)
∂
x
j
=
∑
P
(
j
,
n
1
,
n
2
,
…
,
n
k
,
d
+
K
)
σ
j
′
(
q
j
)
⋅
w
j
,
n
1
⋅
σ
n
1
′
(
q
n
1
)
⋅
w
n
1
,
n
2
⋅
σ
n
2
′
(
q
n
2
)
⋯
w
n
k
,
d
+
K
⋅
σ
d
+
K
′
(
q
d
+
K
)
,
\frac { \partial f ( x ; \theta ) } { \partial x_ j } = \sum _ { \mathcal{P} ( j , n _ { 1 } , n _ { 2 } , \ldots , n _ { k } , d + K ) } \sigma _ { j } ^ { \prime } ( q _ { j } ) \cdot w _ { j , n _ { 1 } } \cdot \sigma _ { n _ { 1 } } ^ { \prime } ( q _ { n _ { 1 } } ) \cdot w _ { n _ { 1 } , n _ { 2 } } \cdot \sigma _ { n _ { 2 } } ^ { \prime } ( q _ { n _ { 2 } } ) \cdots w _ { n _ { k }, d+K } \cdot \sigma _ { d + K } ^ { \prime } ( q _ { d + K } ) ,
∂xj∂f(x;θ)=P(j,n1,n2,…,nk,d+K)∑σj′(qj)⋅wj,n1⋅σn1′(qn1)⋅wn1,n2⋅σn2′(qn2)⋯wnk,d+K⋅σd+K′(qd+K),其中对从
x
j
x_j
xj 到
N
d
+
K
N_{d+K}
Nd+K 的所有路径进行求和.
假设 f ( x ; θ ) f(x; θ) f(x;θ) 的所有激活函数都是 sigmoid 函数。 请注意,如果中间变量 q i q_i qi 的模 ∣ q i ∣ |q_i| ∣qi∣较大,则 σ i ′ ( q i ) σ^{\prime}_i (q_i) σi′(qi) 项将接近于零。 那么对于长路径,包含许多小乘数 σ i ′ ( q i ) σ^{\prime}_i (q_i) σi′(qi)的右侧乘积将非常接近于零。 因此,如果权重为 w i , j w_{i,j} wi,j 的边距离输出神经元较远,则导数 ∂ f ( x ; θ ) ∂ w i , j \frac { \partial f ( x ; \theta ) } { \partial w_{i , j} } ∂wi,j∂f(x;θ)可能非常接近于零,甚至在实际计算中被机器精度下溢。
此外,假设我们有一个损失函数 L ( f ( x ; θ ) ) \mathcal{L}(f(x;θ)) L(f(x;θ)),其中 L ( ⋅ ) \mathcal{L}(\cdot) L(⋅)是可微分的。当使用梯度下降法优化 L \mathcal{L} L时,我们计算的 ∇ θ L ∇_{θ}\mathcal{L} ∇θL 有以下分量: ∇ w i , j L = L ′ ( f ( x ; θ ) ) ⋅ ∂ f ( x ; θ ) ∂ w i , j . \nabla _ { w _ { i , j } } \mathcal{L}= \mathcal{L}^ { \prime } ( f ( x ; \theta ) ) \cdot \frac { \partial f ( x ; \theta ) } { \partial w _ { i , j } } . ∇wi,jL=L′(f(x;θ))⋅∂wi,j∂f(x;θ).因此, ∂ f ( x ; θ ) ∂ w i , j \frac { \partial f ( x ; \theta ) } { \partial w _ { i , j } } ∂wi,j∂f(x;θ)的消失很可能会导致 ∇ w i , j L \nabla _ { w _ { i , j } } \mathcal{L} ∇wi,jL的消失。在这种情况下,参数 w i , j w_{i,j} wi,j 几乎无法通过梯度下降来改变,因此收敛速度会大大减慢。这种梯度消失的问题经常出现在使用 sigmoid 函数的深度神经元网络优化中。解决梯度消失问题的一种有效方法是使用残差神经网络(ResNets)。
权重初始化
在网络层数较少的情况下,将所有权重和偏差初始化为零,或者从零均值的均匀分布或高斯分布中进行采样,通常会提供足够令人满意的收敛结果。 然而,在深度神经网络的情况下,权重的正确初始化会对最优算法的收敛方式产生显着影响。
权重太小/大可能会导致梯度消失或爆炸问题, 这可以从梯度表达式(2.34)中部分地认识到。
如果
σ
j
′
σ^{\prime}_j
σj′ 是有限的并且权重
w
j
i
w_{ji}
wji 的值太小,则长路径的乘积将接近于零,从而导致梯度消失。
另一方面,对于 sigmoid 激活结果,如果
∣
w
j
i
∣
|w_{ji}|
∣wji∣ 较大,
q
j
=
∑
k
∈
P
j
w
k
,
j
y
k
+
b
j
q _ { j } = \sum _ { k \in P _ { j } } w _ { k , j } y _ { k } + b _ { j }
qj=∑k∈Pjwk,jyk+bj 也会很大,使得
σ
j
′
(
q
j
)
σ^{\prime}_j (q_j )
σj′(qj) 接近于零。
从前向传播的观点来看…
权重
w
j
i
w_{ji}
wji 如何的正确初始化?
现在假设信息通过前向传播从第 (ℓ − 1) 层传递到第 ℓ 层,即
y
j
ℓ
=
σ
j
ℓ
(
∑
i
=
1
M
ℓ
−
1
w
j
i
ℓ
y
i
ℓ
−
1
)
,
(2.35)
y _ { j } ^ { \ell } = \sigma _ { j } ^ { \ell} ( \sum _ { i = 1 } ^ { M _ { \ell - 1 } } w _ { j i } ^ { \ell } y _ { i } ^ {\ell - 1 } ) ,\tag{2.35}
yjℓ=σjℓ(i=1∑Mℓ−1wjiℓyiℓ−1),(2.35)
其中 j 是第 ℓ 层神经元的索引。 这里我们省略了偏差
b
b
b。 在实践中,偏差通常被初始化为零或均值为零的随机变量。 为简单起见,我们假设
{
w
i
j
ℓ
}
i
,
j
\{w^ℓ_{ij}\}_{i,j}
{wijℓ}i,j 和
{
y
i
ℓ
−
1
}
i
\{y^{ℓ−1}_i\}_i
{yiℓ−1}i 是两组独立且同分布的均值为零的随机变量。
此外,在前向传播中,
y
i
ℓ
−
1
y^{ℓ−1}_i
yiℓ−1 是通过先前的权重计算的,因此与当前的
w
i
j
ℓ
w^ℓ_{ij}
wijℓ无关,因此它俩是相互独立的。
最终, 我们的目标是找到一种
w
i
j
ℓ
w^ℓ_{ij}
wijℓ的分布,使得第 ℓ 层的输出与它的输入一样分散, 即
Var
(
y
j
ℓ
)
=
Var
(
y
i
ℓ
−
1
)
\text{Var}(y^ℓ_j) = \text{Var}(y^{ℓ−1}_i )
Var(yjℓ)=Var(yiℓ−1)。
我们首先引入以下结论
引理2.3: 如果 X 和 Y 是两个独立的随机变量且
E
[
(
X
)
]
=
E
[
(
Y
)
]
=
0
E[(X)] = E[(Y)] = 0
E[(X)]=E[(Y)]=0,则
Var
(
X
Y
)
=
Var
(
X
)
Var
(
Y
)
\text{Var}(XY ) = \text{Var}(X)\text{Var}(Y )
Var(XY)=Var(X)Var(Y)。
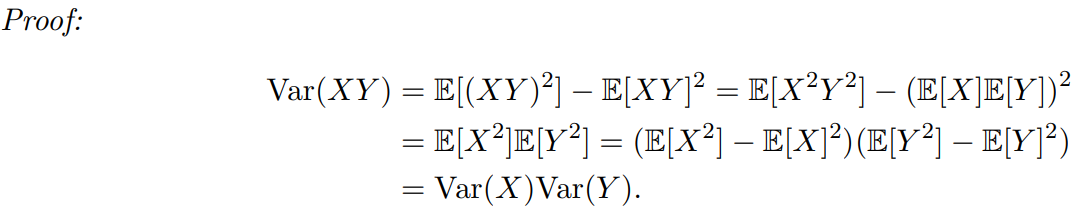
此外,令
f
f
f为可微函数。 然后
f
(
x
)
f(x)
f(x) 在
x
=
E
[
X
]
x = E[X]
x=E[X] 处的线性近似给出
f
(
x
)
≈
f
(
E
[
X
]
)
+
f
′
(
E
[
X
]
)
(
x
−
E
[
X
]
)
.
f ( x ) \approx f ( E \left[ X \right] ) + f ^ { \prime } ( E \left[ X \right] ) ( x - E \left[ X \right] ) .
f(x)≈f(E[X])+f′(E[X])(x−E[X]).用随机变量
X
X
X 替换变量
x
x
x 会得到
f
(
X
)
≈
f
(
E
[
X
]
)
+
f
′
(
E
[
X
]
)
(
X
−
E
[
X
]
)
.
f ( X ) \approx f ( E \left[ X \right] ) + f ^ { \prime } ( E \left[ X \right] ) ( X - E \left[ X \right] ) .
f(X)≈f(E[X])+f′(E[X])(X−E[X]).因此,
Var
(
f
(
X
)
)
≈
Var
(
f
′
(
E
[
X
]
)
(
X
−
E
[
X
]
)
)
=
f
′
(
E
[
X
]
)
2
Var
(
X
)
.
\text{Var}( f ( X ) ) \approx \text{Var} ( f ^ { \prime } ( E \left[ X \right] ) ( X - E \left[ X \right] ) ) = f ^ { \prime } ( E \left[ X \right] ) ^ { 2 } \text{Var} ( X ) .
Var(f(X))≈Var(f′(E[X])(X−E[X]))=f′(E[X])2Var(X).那么带入公式 (2.35) 的数值可知 (
f
→
σ
f\rightarrow\sigma
f→σ,
X
→
w
j
i
ℓ
y
i
ℓ
−
1
X\rightarrow w _ { j i } ^ { \ell } y _ { i } ^ {\ell - 1 }
X→wjiℓyiℓ−1, 且已知
w
j
i
ℓ
w _ { j i } ^ { \ell }
wjiℓ和
y
i
ℓ
−
1
y _ { i } ^ {\ell - 1 }
yiℓ−1相互独立, 故
E
(
w
j
i
ℓ
y
i
ℓ
−
1
)
\mathbb{E}(w _ { j i } ^ { \ell } y _ { i } ^ {\ell - 1 })
E(wjiℓyiℓ−1)是可以分离的. 由假设可得,
E
(
w
j
i
ℓ
)
=
E
(
y
i
ℓ
−
1
)
=
0
\mathbb{E}(w _ { j i } ^ { \ell }) = \mathbb{E}( y _ { i } ^ {\ell - 1 })=0
E(wjiℓ)=E(yiℓ−1)=0):
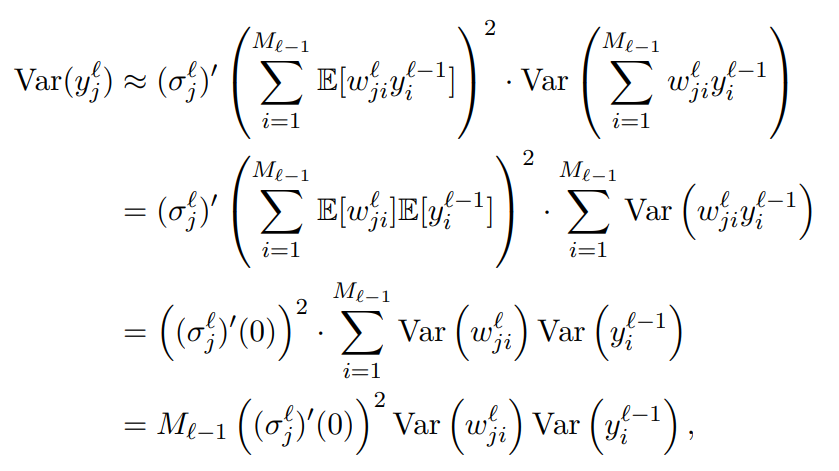
(这里倒数第二个个式子到最后一个式子的原因, 我怀疑是在初始化中, 所有Weight的初始值都是相同的)
因为我们的目标是
Var
(
y
j
ℓ
)
=
Var
(
y
i
ℓ
−
1
)
\text{Var}(y^ℓ_j) = \text{Var}(y^{ℓ−1}_i )
Var(yjℓ)=Var(yiℓ−1), 因此需要
M
ℓ
−
1
(
(
σ
j
ℓ
)
′
(
0
)
)
2
Var
(
w
j
i
ℓ
)
=
1
M _ { \ell - 1 } ( ( \sigma _ { j } ^ {\ell} ) ^ { \prime } ( 0 ) ) ^ { 2 } \text{Var} ( w _ { j i } ^ { \ell } ) = 1
Mℓ−1((σjℓ)′(0))2Var(wjiℓ)=1 故有:
Var
(
w
j
i
ℓ
)
=
1
M
ℓ
−
1
(
(
σ
j
ℓ
)
′
(
0
)
)
2
(2.37)
\text{Var}( w ^ { \ell } _ { j i } ) = \frac { 1 } { M _ { \ell - 1 } \left( ( \sigma ^ { \ell } _ { j } ) ^ { \prime } ( 0 ) \right) ^ { 2 } } \tag{2.37}
Var(wjiℓ)=Mℓ−1((σjℓ)′(0))21(2.37)
因此,我们得到两个有用的结论:
- 如果 w j i ℓ w^{\ell}_{ji} wjiℓ是从正态分布中得出的, 那么 w j i ℓ ∼ N ( 0 , 1 M ℓ − 1 ( ( σ j ℓ ) ′ ( 0 ) ) 2 ) w _ { j i } ^ { \ell } \sim \mathcal{N} ( 0 , \frac { 1 } { M _ { \ell - 1 } ( ( \sigma _ { j } ^ { \ell } ) ^ { \prime } ( 0 ) ) ^ { 2 } } ) wjiℓ∼N(0,Mℓ−1((σjℓ)′(0))21)
- 如果 w j i ℓ w^{\ell}_{ji} wjiℓ是从均匀分布中得出的, 因为 U [ − a , a ] U[-a, a] U[−a,a]的方差是 a 2 3 \frac{a^2}{3} 3a2, 所以有 w j i ℓ ∼ U [ − 3 M ℓ − 1 ( σ j ′ ) ′ ( 0 ) , 3 M ℓ − 1 ( σ j ℓ ) ′ ( 0 ) ] w _ { j i } ^ { \ell } \sim U \left[ - \frac { \sqrt { 3 } } { \sqrt { M _ { \ell - 1 } ( \sigma _ { j } ^ { \prime } ) ^ { \prime } ( 0 ) } } , \frac { \sqrt { 3 } } { \sqrt { M _ { \ell- 1 } ( \sigma _ { j } ^ { \ell} ) ^ { \prime } ( 0 ) } } \right] wjiℓ∼U[−Mℓ−1(σj′)′(0)3,Mℓ−1(σjℓ)′(0)3]
可以发现, 如果要实现网络两层输出值的方差一致, 只需要保证它们之间的边权的初始化服从上述分布即可.
同时, 通过观察方差本身的构成, 我们可以发现这种方差只与 “第一层的结点个数” 和 “第二层的激活函数在0处的导数” 有关.
从反向传播的观点来看…
另一种策略是从反向传播的角度推导的,也称为 Xavier 初始化 [5]。
我们预计:
Var
(
∂
f
(
x
;
θ
)
∂
w
i
j
ℓ
−
1
)
=
Var
(
∂
f
(
x
;
θ
)
∂
w
i
j
ℓ
)
(2.38)
\text{Var}( \frac { \partial f ( x ; \theta ) } { \partial w _ { i j } ^ { \ell - 1 } } ) = \text{Var} ( \frac { \partial f ( x ; \theta ) } { \partial w _ { i j } ^ { \ell } } )\tag{2.38}
Var(∂wijℓ−1∂f(x;θ))=Var(∂wijℓ∂f(x;θ))(2.38)
我们假设 { a i , w j i ℓ } i , j , ℓ \{a_i , w^ℓ_{ji}\}_{i,j,ℓ} {ai,wjiℓ}i,j,ℓ 中的所有权重都是独立且均值为零的同分布随机变量。 另外,我们假设所有激活函数都是恒等的,则关系式 (2.22)-(2.25) 为 p L + 1 = 1 , p i L = p L + 1 a i , (2.39) p ^ { L + 1 } = 1 , p _ { i } ^ { L } = p ^ { L + 1 } a _ { i } ,\tag{2.39} pL+1=1,piL=pL+1ai,(2.39) p i ℓ − 1 = ∑ j = 1 M ℓ p j ℓ w j i ℓ , for ℓ = L , L − 1 , … , 2 (2.40) p _ { i } ^ { \ell - 1 } = \sum _ { j = 1 } ^ { M _ { \ell } } p _ { j } ^ { \ell } w _ { j i } ^ { \ell} , \text{ for }\ \ell= L , L - 1 , \ldots , 2 \tag{2.40} piℓ−1=j=1∑Mℓpjℓwjiℓ, for ℓ=L,L−1,…,2(2.40)
通过回溯递归,
p
j
ℓ
p_j^\ell
pjℓ是由
{
w
j
i
ℓ
+
1
}
i
,
j
∪
⋯
∪
{
w
j
i
L
}
i
,
j
∪
{
a
i
}
i
\{w^{\ell+1}_{ji}\}_{i,j} \cup \cdots \cup \left\{ w _ { j i } ^ { L } \right\} _ { i , j } \cup \left\{ a _ { i } \right\} _ { i }
{wjiℓ+1}i,j∪⋯∪{wjiL}i,j∪{ai}i确定的而非独立的
{
w
j
i
ℓ
}
i
,
j
\{w^\ell_{ji}\}_{i,j}
{wjiℓ}i,j和
{
y
ℓ
−
1
}
i
\{y^{\ell-1}\}_i
{yℓ−1}i (这俩者是
p
j
ℓ
p_j^\ell
pjℓ左侧的边权和输出).
因此,
p
j
ℓ
p _ { j } ^ { \ell }
pjℓ与
w
j
i
ℓ
w _ { j i } ^ { \ell }
wjiℓ之间是彼此独立的, 故:
E
[
∑
j
=
1
M
ℓ
p
j
ℓ
w
j
i
ℓ
]
=
∑
j
=
1
M
ℓ
E
[
p
j
ℓ
]
E
[
w
j
i
ℓ
]
=
0
,
\mathbb{E} \left[ \sum _ { j = 1 } ^ { M _ { \ell } } p _ { j } ^ { \ell } w _ { j i } ^ { \ell } \right] = \sum _ { j = 1 } ^ { M _ { \ell } } \mathbb{E} \left[ p _ { j } ^ { \ell } \right] \mathbb{E} \left[ w _ { j i } ^ { \ell } \right] = 0 ,
E[j=1∑Mℓpjℓwjiℓ]=j=1∑MℓE[pjℓ]E[wjiℓ]=0,因为所有权重都是均值为零的同分布随机变量, 故
E
[
w
j
i
ℓ
]
=
0
\mathbb{E}[w_{ji}^{\ell}]=0
E[wjiℓ]=0, 由上式可得,
E
[
p
i
ℓ
−
1
]
=
0
\mathbb{E}[p^{ℓ−1}_i] = 0
E[piℓ−1]=0,类似地,
E
[
p
i
ℓ
]
=
0
\mathbb{E}[p^ℓ_i] = 0
E[piℓ]=0.
此外,由于 y j ℓ = ∑ i = 1 M ℓ − 1 w j i ℓ y i ℓ − 1 y _ { j } ^ { \ell } = \sum _ { i = 1 } ^ { M _ { \ell - 1 } } w _ { j i } ^ { \ell } y _ { i } ^ { \ell - 1 } yjℓ=∑i=1Mℓ−1wjiℓyiℓ−1 且 w j i ℓ w^ℓ_{ji} wjiℓ 与 y i ℓ − 1 y^{ℓ−1}_i yiℓ−1 无关 (前向传播的结论),故 E [ y j ℓ ] = ∑ i = 1 M ℓ − 1 E [ w j i ℓ ] E [ y i ℓ − 1 ] = 0. \mathbb{E}[ y _ { j } ^ { \ell } ] = \sum _ { i = 1 } ^ { M _ { \ell - 1} } \mathbb{E} [ w _ { j i } ^ { \ell } ] \mathbb{E} [ y _ { i } ^ { \ell - 1 } ] = 0. E[yjℓ]=i=1∑Mℓ−1E[wjiℓ]E[yiℓ−1]=0.
类似地, E [ y j ℓ − 1 ] = E [ y j ℓ − 2 ] = 0 \mathbb{E}[y_j^{\ell-1}]=\mathbb{E}[y_j^{\ell-2}]=0 E[yjℓ−1]=E[yjℓ−2]=0.
现在,对于
ℓ
≥
2
ℓ ≥ 2
ℓ≥2,通过(2.29),目标(2.38)可被写为
Var
(
p
j
ℓ
−
1
y
i
ℓ
−
2
)
=
Var
(
p
j
ℓ
y
i
ℓ
−
1
)
\text{Var}(p_j^{\ell-1}y_i^{\ell-2}) = \text{Var}(p^\ell_j y_i^{\ell-1})
Var(pjℓ−1yiℓ−2)=Var(pjℓyiℓ−1)
使用引理 2.3 令:
Var
(
p
j
ℓ
−
1
)
Var
(
y
i
ℓ
−
2
)
=
Var
(
p
j
ℓ
)
Var
(
y
i
ℓ
−
1
)
.
\text{Var}( p _ { j } ^ { \ell- 1 } ) \text{Var}( y _ { i } ^ { \ell- 2 } ) = \text{Var}( p _ { j } ^ { \ell} ) \text{Var}( y _ { i } ^ { \ell- 1 } ) .
Var(pjℓ−1)Var(yiℓ−2)=Var(pjℓ)Var(yiℓ−1).
如上所述,我们还期望
Var
(
y
i
ℓ
−
2
)
=
Var
(
y
i
ℓ
−
1
)
\text{Var}(y^{ℓ−2}_i ) = \text{Var}(y^{ℓ−1}_i)
Var(yiℓ−2)=Var(yiℓ−1) (基于前向传播的目标),因此下式必须成立
Var
(
p
j
ℓ
−
1
)
=
Var
(
p
j
ℓ
)
.
(2.41)
\text{Var}( p _ { j } ^ { \ell - 1 } ) = \text{Var}( p _ { j } ^ { \ell } ). \tag{2.41}
Var(pjℓ−1)=Var(pjℓ).(2.41)
对(2.40)进行取方差的操作, 即
Var
(
⋅
)
\text{Var}(\cdot)
Var(⋅). 以及引入引理2.3. 可得:
Var
(
p
i
ℓ
−
1
)
=
∑
j
=
1
M
ℓ
Var
(
p
j
ℓ
)
Var
(
w
j
i
ℓ
)
=
M
ℓ
Var
(
p
j
ℓ
)
Var
(
w
j
i
ℓ
)
,
(2.42)
\text{Var} ( p _ { i } ^ { \ell - 1 } ) = \sum _ { j = 1 } ^ { M _ { \ell } } \text{Var}( p _ { j } ^ { \ell } ) \text{Var} ( w _ { j i } ^ { \ell } ) = M _ { \ell} \text{Var}( p _ { j } ^ { \ell } ) \text{Var}( w _ { j i } ^ { \ell} ) ,\tag{2.42}
Var(piℓ−1)=j=1∑MℓVar(pjℓ)Var(wjiℓ)=MℓVar(pjℓ)Var(wjiℓ),(2.42)
其中我们使用了
{
p
j
ℓ
}
j
\{p^ℓ_j\}_j
{pjℓ}j 同分布这一事实。 结合(2.41)和(2.42),我们有
Var
(
w
j
i
ℓ
)
=
1
M
ℓ
.
(2.43)
\text{Var} ( w _ { j i } ^ { \ell} ) = \frac { 1 } { M _ { \ell } } .\tag{2.43}
Var(wjiℓ)=Mℓ1.(2.43)
关系式(2.43)表示
w
j
i
ℓ
w^ℓ_{ji}
wjiℓ 的方差与第ℓ层的宽度成反比。 相比之下,在线性激活函数的假设下,关系式(2.37)变为
Var
(
w
j
i
ℓ
)
=
1
M
ℓ
−
1
,
(2.44)
\text{Var} ( w _ { j i } ^ { \ell} ) = \frac { 1 } { M _ { \ell - 1 } } ,\tag{2.44}
Var(wjiℓ)=Mℓ−11,(2.44)
这意味着
w
j
i
ℓ
w^ℓ_{ji}
wjiℓ 的方差与 ℓ−1 层的宽度成反比.
现在,只有在 M ℓ = M ℓ − 1 M_ℓ = M_{ℓ−1} Mℓ=Mℓ−1 的情况下 (即当任意两个连续层的宽度相同时),(2.43)和(2.44)同时满足。 由于这个条件限制太多,一个有利可图的折衷方案是取两者的调和平均值,在这种情况下有 Var ( w j i ℓ ) = 2 M ℓ + M ℓ − 1 . \text{Var} ( w _ { j i } ^ { \ell } ) = \frac { 2 } { M _ { \ell } + M _ { \ell - 1 } } . Var(wjiℓ)=Mℓ+Mℓ−12.
再次, 我们得到两个具有实际意义的结论:
- 如果 w j i ℓ w^{\ell}_{ji} wjiℓ是从正态分布中得出的, 那么 w j i ℓ ∼ N ( 0 , 2 M ℓ + M ℓ − 1 ) w _ { j i } ^ { \ell } \sim \mathcal{N} ( 0 , \frac { 2 } { M _ { \ell } + M _ { \ell - 1 } } ) wjiℓ∼N(0,Mℓ+Mℓ−12)
- 如果 w j i ℓ w^{\ell}_{ji} wjiℓ是从均匀分布中得出的, 因为 U [ − a , a ] U[-a, a] U[−a,a]的方差是 a 2 3 \frac{a^2}{3} 3a2, 所以有 w j i ℓ ∼ U [ − 6 M ℓ + M ℓ − 1 , 6 M ℓ + M ℓ − 1 ] w _ { j i } ^ { \ell } \sim U \left[ - \frac { \sqrt { 6 } } { \sqrt { M _ { \ell} + M _ { \ell - 1 } } } , \frac { \sqrt { 6 } } { \sqrt { M _ { \ell}+ M _ { \ell- 1 } } } \right] wjiℓ∼U[−Mℓ+Mℓ−16,Mℓ+Mℓ−16]