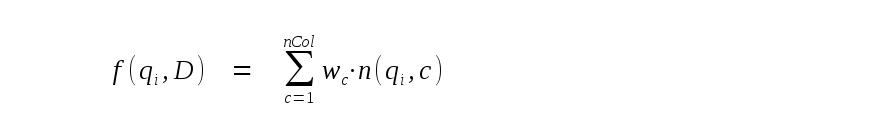文章目录
- 1. 概述
- 2. 静态空间管理缺点
- 3. 动态空间管理
- 3.1 扩容
- 3.1.1 如何实现扩容
- 3.1.2 扩容算法
- 3.1.3 容量递增策略 VS 容量倍增策略
- 3.1.3.1 容量倍增策略分摊分析
- 3.1.3.2 容量递增策略分摊分析
- 3.1.3.3 结果对比
- 3.2缩容
- 3.2.1 动态缩容算法实现
- 3.2.2 动态缩容算法时间复杂度
- 4. 总结
1. 概述
介绍动态空间管理策略
2. 静态空间管理缺点
静态空间管理的空间效率难以保证。

难题可归纳为:
如何才能保证向量的装填因子既不致于超过1,也不致于太接近于0?
3. 动态空间管理
3.1 扩容
3.1.1 如何实现扩容
另申请一个容量更大的数组,并将原数组中的成员集体搬迁至新的空间,释放原数组占用空间。

3.1.2 扩容算法
结论:新数组的容量总是取作原数组的两倍
template <typename T> void Vector<T>::expand() { //向量空间不足时扩容
if ( _size < _capacity ) return; //尚未满员时,不必扩容
if ( _capacity < DEFAULT_CAPACITY ) _capacity = DEFAULT_CAPACITY; //不低于最小容量
T* oldElem = _elem; _elem = new T[_capacity <<= 1]; //容量加倍
for ( Rank i = 0; i < _size; i++ )
_elem[i] = oldElem[i]; //复制原向量内容(T为基本类型,或已重载赋值操作符'=')
/*DSA*/ //printf("\n_ELEM [%x]*%d/%d expanded and shift to [%x]*%d/%d\n", oldElem, _size, _capacity/2, _elem, _size, _capacity);
delete [] oldElem; //释放原空间
}
为何采用容量加倍策略呢?其他策略是否可行?
3.1.3 容量递增策略 VS 容量倍增策略
分析方法:分摊分析 而不是平均分析,对这两种分析情况不清楚可以看复杂度分析
若采用平均分析,则很可能因为所做的概率分布假定与实际不符,而导致不准确的结论。比如若采用通常的均匀分布假设,认为扩容与不扩容事件的概率各半,则会得出该策略效率极低的错误结论。实际上,只要假定这两类事件出现的概率各为常数,就必然导致这种误判。而实际情况是,采用加倍扩容策略后,在其生命期内随着该数据结构的容量不断增加,扩容事件出现的概率将以几何级数的速度迅速趋近于零。对于此类算法和数据结构,唯有借助分摊分析,方能对其性能做出综合的客观评价。
分析要求:参与分摊的操作必须构成和来自一个真实可行的操作序列,而且该序列还必须足够地长。
以可扩充向量为例,可以考查对该结构的连续n次(查询、插入或删除等)操作,将所有操作中用于内部数组扩容的时间累计起来,然后除以n。只要n足够大,这一平均时间就是用于扩容处理的分摊时间成本。
考查最坏的情况,假设在此后需要连续地进行n次insert()操作。
3.1.3.1 容量倍增策略分摊分析

几何级数不熟悉的看算法分析
1+2 + 4 + … +
2
∣
l
o
g
2
(
n
−
1
)
∣
2^{|log_2(n-1)|}
2∣log2(n−1)∣ = O(
2
∣
l
o
g
2
(
n
−
1
)
∣
2^{|log_2(n-1)|}
2∣log2(n−1)∣) = O(n)
扩容的均摊分析为O(1)。
3.1.3.2 容量递增策略分摊分析

对算术级数不熟悉的看算法分析
3.1.3.3 结果对比
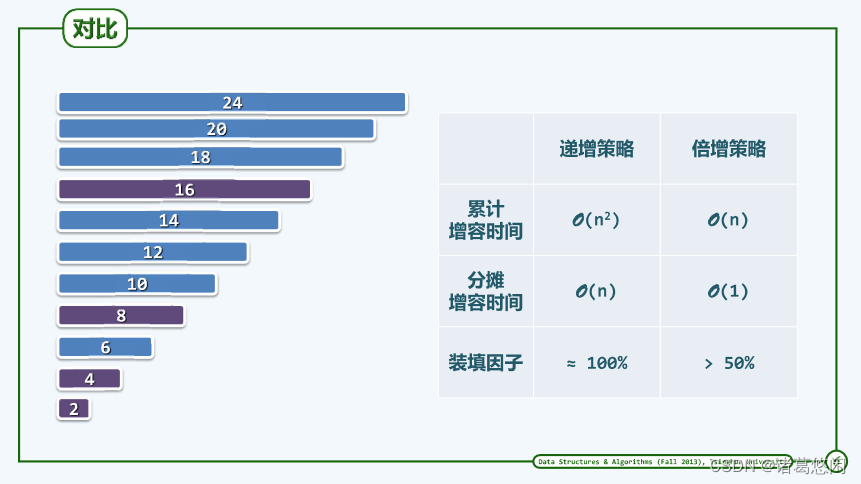
3.2缩容
导致低效率的另一情况是,向量的实际规模可能远远小于内部数组的容量。
3.2.1 动态缩容算法实现
算法思想:
每次删除操作之后,一旦空间利用率已降至某一阈值以下,该算法随即申请一个容量减半的新数组,将原数组中的元素逐一搬迁至其中,最后将原数组所占空间交还操作系统。
这里以25%作为装填因子的下限,但在实际应用中,为避免出现频繁交替扩容和缩容的情况,可以选用更低的阈值,甚至取作0(相当于禁止缩容)。
template <typename T> void Vector<T>::shrink() { //装填因子过小时压缩向量所占空间
if ( _capacity < DEFAULT_CAPACITY << 1 ) return; //不致收缩到DEFAULT_CAPACITY以下
if ( _size << 2 > _capacity ) return; //以25%为界
T* oldElem = _elem; _elem = new T[_capacity >>= 1]; //容量减半
for ( Rank i = 0; i < _size; i++ ) _elem[i] = oldElem[i]; //复制原向量内容
delete[] oldElem; //释放原空间
}
3.2.2 动态缩容算法时间复杂度
与expand()操作类似,尽管单次shrink()操作需要线性量级的时间,但其分摊复杂度亦为O(1)。
4. 总结
就单次扩容或缩容操作而言,所需时间的确会高达Ω(n),因此在对单次操作的执行速度极其敏感的应用场合以上策略并不适用,其中缩容操作甚至可以完全不予考虑。