常用的时间序列分析方法总结和代码示例

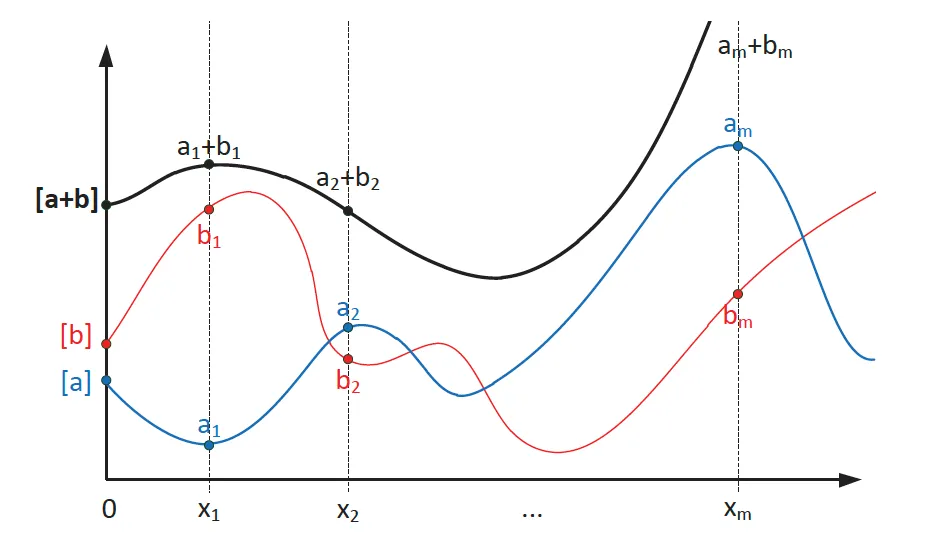
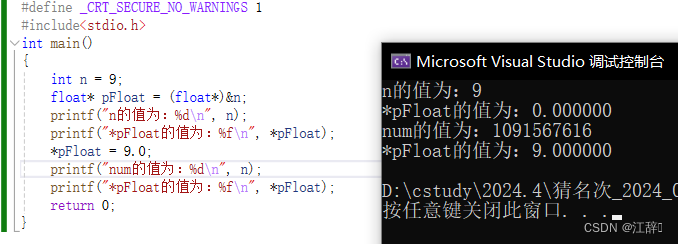
时间序列是最流行的数据类型之一。视频，图像，像素，信号，任何有时间成分的东西都可以转化为时间序列。

在本文中将在分析时间序列时使用的常见的处理方法。这些方法可以帮助你获得有关数据本身的见解，为建模做好准备并且可以得出一些初步结论。

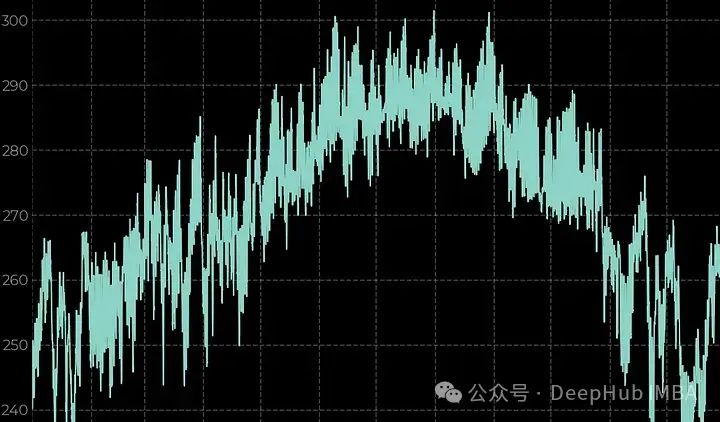
我们将分析一个气象时间序列。利用逐时ERA5 Land[1]研究2023年西伯利亚东南部点的2 m气温、总降水量、地表净太阳辐射和地表压力。

首先我们导入相关的库：

 import pandas as pd
 import seaborn as sns
 import numpy as np
 
 import matplotlib.pyplot as plt
 import xarray as xr
 
 import statsmodels.api as sm
 from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
 from scipy import stats

matplotlib是可以设置不同的风格的，这里我们使用 opinionated和 ambivalent来进行风格的设置

 from ambivalent import STYLES
 import opinionated
 plt.style.use(STYLES['ambivalent'])
 plt.style.use("dark_background")

折线图

要观察一个时间序列，最简单的方法就是折线图。为了处理地理空间多维数组，我们将使用xarray库。

 data = xr.open_dataset('Medium_data.nc')
 data

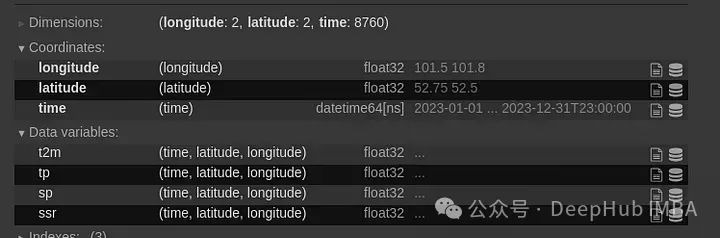
现在我们需要针对所选位置对数据进行切片，并将其转换为pandas DF，并创建一个线形图:

 df = data.sel(latitude=52.53, longitude=101.63, method='pad').to_pandas().drop(['latitude', 'longitude'], axis=1)
 fig, ax = plt.subplots(ncols = 2, nrows = 2, figsize=(16,9))
 df['t2m'].plot(ax=ax[0,0])
 ax[0,0].set_title('Air Temperature')
 df['ssr'].plot(ax=ax[0,1])
 ax[0,1].set_title('Surface Net Solar Radiation')
 df['sp'].plot(ax=ax[1,0])
 ax[1,0].set_title('Surface Pressure')
 df['tp'].plot(ax=ax[1,1])
 ax[1,1].set_title('Total Precipitation')
 plt.tight_layout()
 plt.show()

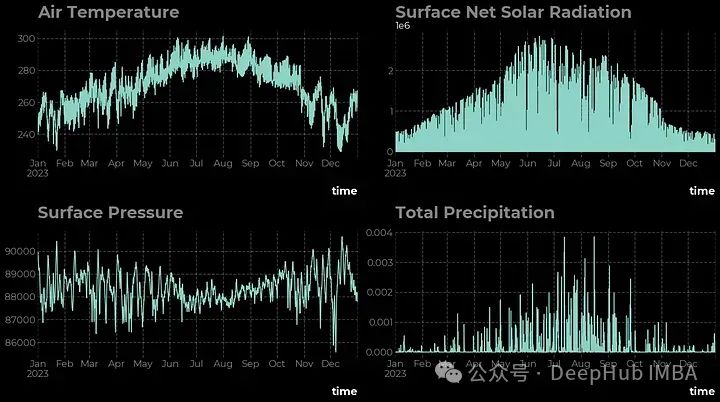
从线形图中可以清楚地看出，所有四个时间序列都有不同的特征，下面让我们使用数学工具来研究它们。

分解与平稳性

任何时间序列都有三个重要属性需要考虑:

1、趋势是时间序列中平稳的长期变化;

2、季节性指的是一个时间序列的平均值有规律的周期性变化;

3、噪声(残差)，它是均值为零的信号的随机成分。

为了分别得到这些成分，可以使用经典分解(加性或乘法)。该操作是通过应用卷积滤波器产生的，因此每个时间序列分量被定义为

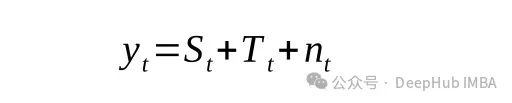
或者

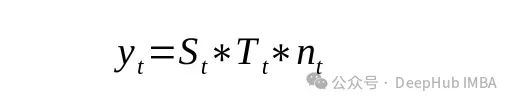
这里的y为时间序列的值，S为季节分量，T为趋势分量，n为噪声。

为了进行分解，除了选择分解类之外，还需要设置一个季节周期(例如，p=1表示年度数据，p=4表示季度数据，p=12表示月度数据等)。

前面提到的经典分解是一种非常幼稚和简单的方法。它具有明显的局限性，如线性，无法捕捉动态季节性和难以处理时间序列中的非平稳性，但是就本文作为演示，这种方法是可以的。

为了进行经典的分解，我们将使用statmodels库中的seasonal_decomposition函数，周期等于24，因为我们处理的是每小时的数据:

 vars = {'t2m': 'Air Temperature', 'tp': 'Total Precipitation', 'sp': 'Surface Pressure', 'ssr': 'Surface Net Solar Radiation'}
 for var in df.columns:
   result = sm.tsa.seasonal_decompose(df[var], model='additive', period = 24)
   results_df = pd.DataFrame({'trend': result.trend, 'seasonal': result.seasonal, 'resid': result.resid, 'observed': result.observed})
   fig, ax = plt.subplots(ncols = 2, nrows = 2,figsize=(16,9))
   ax[0,0].plot(df.index, results_df.trend)
   ax[0,0].set_title('Trend')
   ax[0,0].set_ylabel('Value')
 
   ax[0,1].plot(df.index, results_df.seasonal)
   ax[0,1].set_title('Seasonal')
 
   ax[1,0].plot(df.index, results_df.resid)
   ax[1,0].set_title('Residual')
   ax[1,0].set_ylabel('Value')
   ax[1,0].set_xlabel('time')
 
   ax[1,1].plot(df.index, results_df.observed)
   ax[1,1].set_title('Observed')
   ax[1,1].set_xlabel('time')
 
   opinionated.set_title_and_suptitle(vars[var], f"Dickey-Fuller test: {round(sm.tsa.stattools.adfuller(df[var])[1],5)}", position_title=[0.45,1],
                                      position_sub_title=[0.95, 1])
   plt.tight_layout()
   plt.savefig(f'Seasonal_{var}.png')
   plt.show()

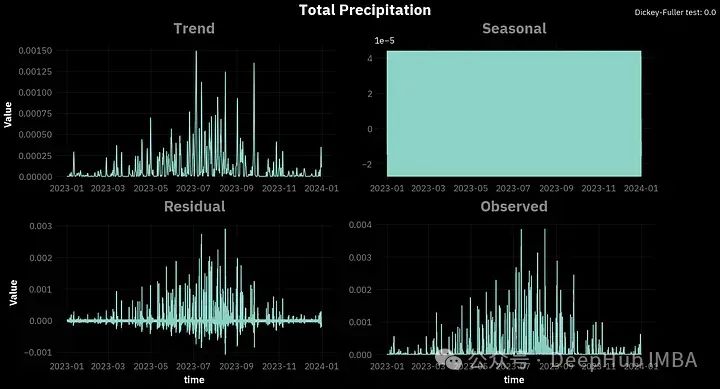
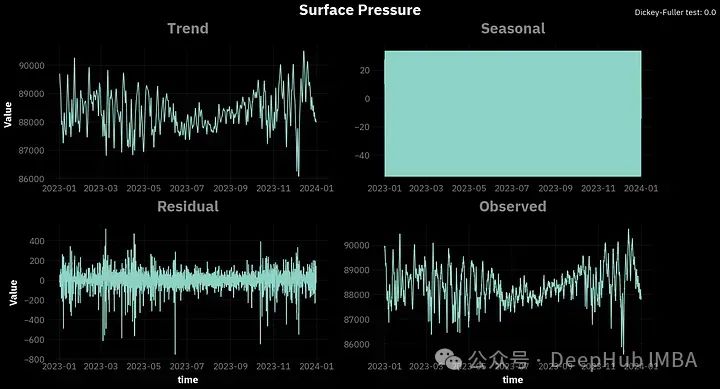
你可以看到，对于所有的变量，季节性因素看起来都很混乱。这是因为我们分析的是每小时的数据，这些季节变化是在一天内观察到的，并没有直接的关联。所以我们可以尝试将数据重新采样到每日间隔，并在一天的时间段内进行分解。

 df_d = df.resample('1d').mean()

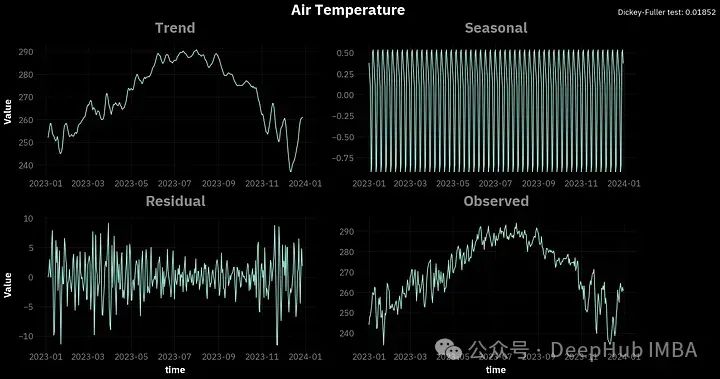
请注意到图表右上角的Dickey-Fuller(ADF) 。这是一个平稳性测试，使用的是adfuller函数。对于时间序列，平稳性意味着时间序列的属性不随时间变化。我们这里说的属性是指：方差、季节性、趋势和自相关性。

Dickey-Fuller (ADF)检验的流程是：提出时间序列是非平稳的零假设。然后我们选择显著性水平α，通常为5%。α是错误地拒绝零假设的概率，而零假设实际上是正确的。所以在我们的例子中，α=5%有5%的风险得出时间序列是平稳的，而实际上不是。

测试结果会给出一个p值。如果小于0.05，我们可以拒绝零假设。可以看到，根据ADF检验所有4个变量都是平稳的。

一般情况下要应用时间序列预测模型，如ARIMA等，平稳性是必须的。这也是我们选择气象数据的原因，因为它们在大多数情况下是平稳的，所以才会出现在不同的时间序列相关的学习材料中进行分析。

分布

在得出所有时间序列都是平稳的结论之后，让我们来看看它们是如何分布的。我们将使用著名的seaborn库及其函数pairplot，该函数允许使用历史和kde创建信息丰富的图。

 ax = sns.pairplot(df, diag_kind='kde')
 ax.map_upper(sns.histplot, bins=20)
 ax.map_lower(sns.kdeplot, levels=5, color='.1')
 plt.show()

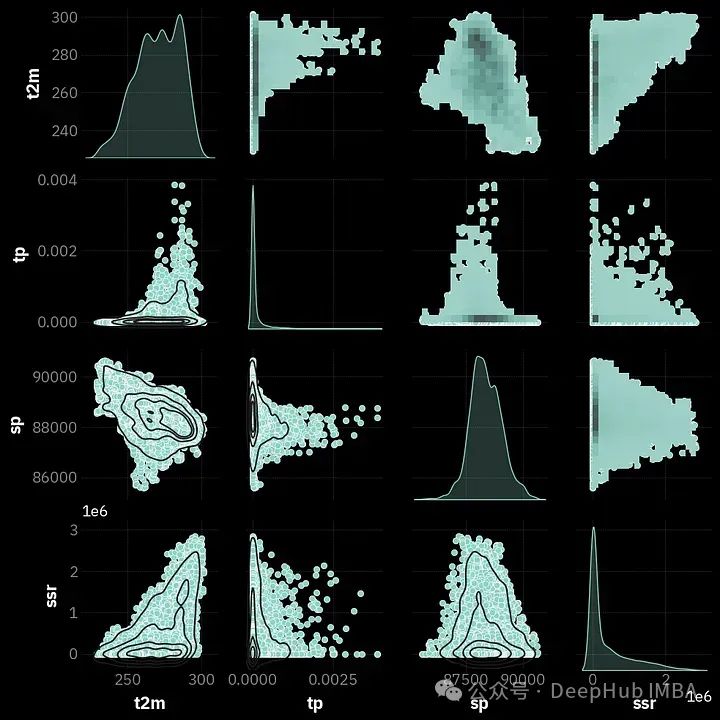
让我们考虑t2m(1行1列)的示例。在分析核密度估计(kde)图时，很明显这个变量的分布是多模态的，这意味着它由2个或更多的“钟形”组成。在本文的后续阶段中，我们将尝试将变量转换为类似于正态分布的形式。

第一列和第一行中的其他图是相同的，但它们的可视化方式不同。这些是散点图，可以确定两个变量是如何相关的。所以一个点的颜色越深，或者离中心圆越近，这个区域内点的密度就越高。

Box-Cox转换

由于我们已经发现气温时间序列是平稳的，但不是正态分布，所以可以尝试使用Box-Cox变换来修复它。这里使用scipy包及其函数boxcox。

 df_d['t2m_box'], _ = stats.boxcox(df_d.t2m)
 fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,7))
 sns.histplot(df_d.t2m_box, kde=True, ax=ax[0])
 sns.histplot(df_d.t2m, kde=True, ax=ax[1])

图的左边部分是经过BoxCox变换后的时间序列分布，可以看到，它还远远不能被称为“正态”分布。但是如果我们把它和右边的比较，我们可以说的确更接近于“正态”。

我们还可以做的另一件事是确保执行的转换是有用的，可以创建一个概率图：绘制理论分布的分位数(在我们的情况下是正态)与经验数据的样本(即我们考虑的时间序列)。越靠近白线的点越好。

 fig = plt.figure()
 
 ax1 = fig.add_subplot(211)
 prob = stats.probplot(df_d.t2m, dist=stats.norm, plot=ax1)
 ax1.get_lines()[1].set_color('w')
 ax1.get_lines()[0].set_color('#8dd3c7')
 ax1.set_title('Probplot against normal distribution')
 
 ax2 = fig.add_subplot(212)
 prob = stats.probplot(df_d.t2m_box, dist=stats.norm, plot=ax2)
 ax2.get_lines()[1].set_color('w')
 ax2.get_lines()[0].set_color('#8dd3c7')
 ax2.set_title('Probplot after Box-Cox transformation')
 plt.tight_layout()fig = plt.figure()
 
 ax1 = fig.add_subplot(211)
 prob = stats.probplot(df_d.t2m, dist=stats.norm, plot=ax1)
 ax1.set_title('Probplot against normal distribution')
 
 ax2 = fig.add_subplot(212)
 prob = stats.probplot(df_d.t2m_box, dist=stats.norm, plot=ax2)
 ax2.set_title('Probplot after Box-Cox transformation')
 plt.tight_layout()

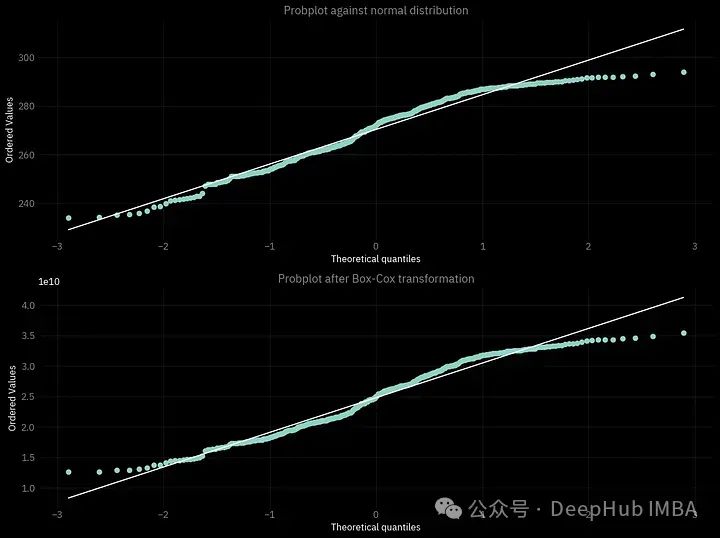
这个概率图还有一个更常见的名字QQ图

另外需要说明的是，如果打算使用转换后的时间序列进行ML建模，不要忘记应用反向BoxCox转换，这样才能的到最终的正确结果。

自相关

时间序列分析的最后一步是自相关。自相关函数(ACF)估计时间序列和滞后版本之间的相关性。或者换句话说，时间序列的特定值如何与不同时间间隔内的其他先验值相关联。绘制部分自相关函数(PACF)也可能有所帮助，它与自相关相同，但删除了较短滞后的相关性。它估计某个时间戳内值之间的相关性，但控制其他值的影响。

 for var in df.columns[:-1]:
   fig, (ax1, ax2) = plt.subplots(2,1,figsize=(10,8))
   plot_acf(df_d.t2m, ax = ax1)
   plot_pacf(df_d.t2m, ax = ax2)
   opinionated.set_title_and_suptitle(vars[var], '',position_title=[0.38,1],
                                      position_sub_title=[0.95, 1])
   plt.tight_layout()
   plt.show()

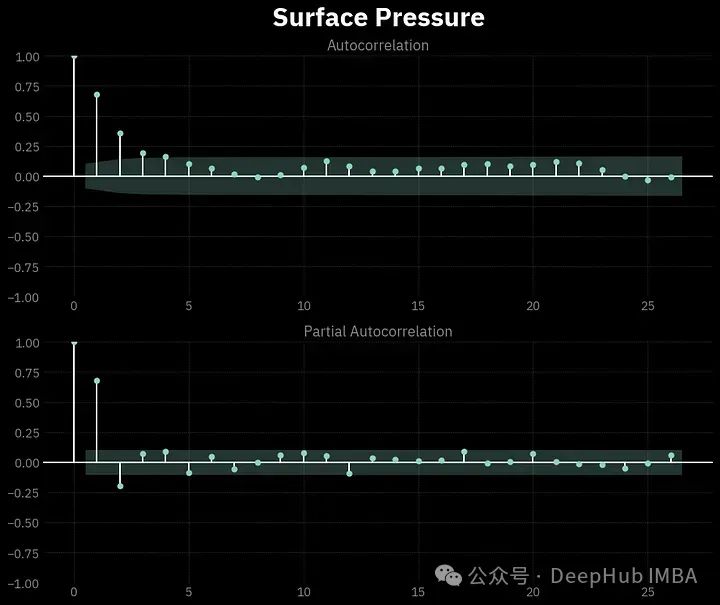
可以看到在地表压力时间序列中有一个非常强的部分自相关，有1天的滞后。然后明显减弱，3天后几乎消失。这样的分析可以帮助我们更好地理解正在处理的数据的性质，从而得出更有意义的结论。

总结

以上就是在处理时间序列时进行探索性数据分析时常用的方法，通过上面这些方法可以很好的了解到时间序列的信息，为我们后面的建模提供数据的支持。

本文数据：

[1] Muñoz Sabater, J. (2019): ERA5-Land hourly data from 1950 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). DOI: 10.24381/cds.e2161bac

https://avoid.overfit.cn/post/d5229e3c8e464859be9f08bdce612676

作者：Aleksei Rozanov