t检验、方差分析（ANOVA）等参数检验都有一个共同的前提条件：样本数据必须服从正态分布，即样本数据必须来源于一个正态分布的总体，若样本数据不服从正态分布，就不能用以上参数检验对数据进行分析，而应该使用非参数检验（如卡方检验、置换检验等）

参数检验：t检验、方差分析（ANOVA）
非参数检验：正态检验

1.描述性统计法

图示法：
直方图(with 拟合正态分布曲线)-[注: 数据量少慎用]
QQ图：拟合优度 样本数据直方图和正态分布图之间 (当QQ图上的点都大致落在$一条直线上$时，表示高度正相关，即这些数据是正态分布的。)

$\bullet$ QQ图
利用Q-Q图来对数据进行正态分布的检验，则可以令x轴为正态分布的分位数，y轴为样本分位数，如果这两者构成的点分布在一条直线上，就证明样本数据与正态分布存在线性相关性，即服从正态分布。 且该直线的斜率为标准差,截距为均值.

2.概率统计法

(1) 基于经验分布函数（empirical distribution function,EDF）
①Kolmogorov–Smirnov test
计算出$经验分布和理论分布$之间的距离，并将其中最大的距离（差异）作为检验统计量
样本量>2000
需要指定总体的均值和方差
$\cdot$ 可用于检验其他任何分布

②Lilliefors test
$通过计算经验分布函数与累积分布函数$之间的最大差异来进行检验
直接利用样本的均值和方差进行计算
最适用于$\text{对称分布的小样本}$,也适用于大样本
$\cdot$ 只适用于正态性检验。

③Anderson–Darling test (AD)
通过计算数据的$累积分布曲线与理想正态分布的累积分布$曲线之间的差异来进行检验,且考虑了两条累积分布曲线之间的所有差异(比K-S检验效果更好)
仅适用于小样本，推荐<26。但有些超过200的工业数据也有可能通过A-D检验。
$\cdot$ 可用于检验其他分布。

（2）基于卡方分布（Chi-squared distribution）
①D’Agostino’s K-squared test （Skewness-Kurtosis test）
通过计算偏度（Skewness）和峰度（Kurtosis）来量化数据分布曲线与标准正态分布曲线之间的差异与不对称性，
适用于大样本
$\cdot$ 仅能用于正态性检验。

②Jarque–Bera test
必须用于大样本（matlab提到样本量小于2000时，显著性水平会从0.001跌到0.5），
$\cdot$ 只能用于正态性检验。

（3）基于回归和相关（regression- and correlation-based）
①Shapiro–Wilk test(SW)
最有效 在每一个样本值都是唯一时的检验效果最好，但若样本中存在几个值重复的情况下该方法便会大打折扣。因此该方法只适用于小样本，推荐样本量为7~2000。当样本量超过5000时不再适用
matlab函数源下载

常用选择方法：
（1）当样本量较大时通常会选择 K-S-L test 或 D’Agostino’s K-squared test
（2）当样本量较小时通常选用 AD test 或 SW test

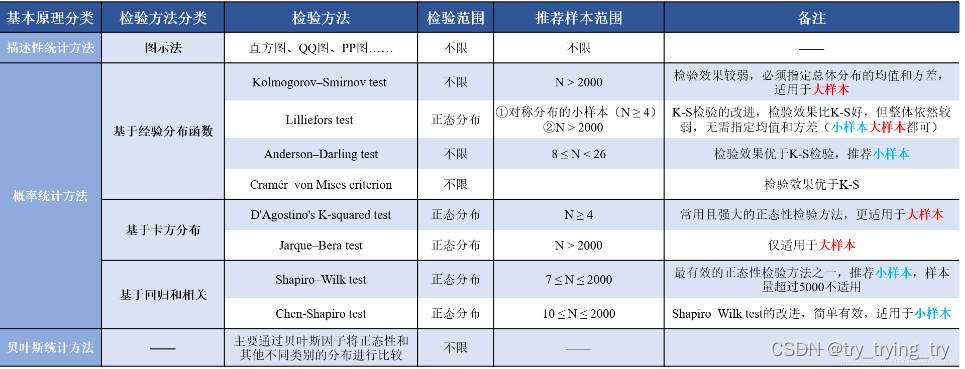
经验：

1. 在实际操作中可以根据样本量大小选择多种检验方法进行正态性检验，同时通过QQ图等图示法辅助判断；

参考：
正态性检验总结 特别特别地好