什么是并查集
并查集是一种数据结构,主要能够高效地实现以下两个功能
给出图中任意两点a,b:
- union(a,b) :将a,b所在的集合合并起来
- isConnected(a,b) :问这a,b两点能否通过任意路径连接起来
同时也能支持:
- size() :返回并查集中有多少个集合
为什么并查集快
我们也可以先求出两个节点的路径,只要有路径,那么就是连接的,否则就是不连接的
但回答两个节点是否连接,比回答两个节点的路径是什么,需要的信息更少
如果只想知道两个节点是否连接,但却耗费了更多的资源去求解两个节点的路径是什么,而这部分我们并不关心
这就是并查集快的原因:只计算和保存需要的信息
快速查找
假设图中有N个节点,每个节点的编号为0~N-1
则每个节点属于哪个集合,可以用数组int[] parent表示:

上图中,编号为0,1,2的节点属于编号为0的集合,编号为3,4的节点属于编号为1的集合
isConnected
这样判断a,b是否属于同一个集合,即是否已连接,只用判断parent[a] == parent[b]即可
union
但如果想好将两个集合合并,就比较麻烦
例如,需要将编号为2,3节点所在的集合合并,就需要:
- 找到节点2,3所属集合的编号,分别为0,1,集合编号不同,需要合并
- 遍历parent数组,要么将所有编号为0的节点的集合编号改为1,要么将1改为0
可以发现这种方式实现并查集,查找很快,但合并很慢,因为需要遍历所有的节点
快速合并
第二种实现方式,将并查集中每个节点相连接,形成树的结构
这棵树由孩子指向父亲,如果每棵树代表一个集合,用树的根节点来标识一个集合
这样当判断两个节点是否属于同一集合时,需要从当前节点往上,一直找到根节点,如果根节点相同,说明属于同一个集合

如上图所示,节点2指向节点3,节点3指向自己,因此节点3是该集合的根节点
还是用parent数组表示所有的集合,对应到上图的示例为:parent[2] = 3,parent[3] = 3
isConnected
判断两个节点是否属于同一集合的操作为:
- 从每个节点开始,不断往上找,直到找到根节点为止
- 如果根节点相同,则属于同一集合
public boolean isConnected(int a,int b) {
return find(a) == find(b);
}
public int find(int v) {
int cur = v;
while (cur != p[cur]) {
cur = p[cur];
}
return cur;
}
union
合并两个集合:
- 找到节点a,b所属集合的根节点parentA,parentB
- 将parentB挂到parentB下面即可,
parent[parentA] = parentB
例如:下图将根节点为5的集合,合并到根节点为3的集合中,合并后,根节点为5的结合中的所有节点的根节点变为3

代码为:
public void union(int a,int b){
int pa = find(a);
int pb = find(b);
if (pa != pb) {
p[pa] = pb;
}
}
这种实现方式合并和查找的时间复杂度为O(h),h为树的高度
合并时不用像上一种方法一样,遍历所有的节点,开销较低,但是查找需要遍历当前节点所在的树
因此优化方向为,降低树的高度
基于size的优化
要降低树的高度,可以考虑在union时,是将parentA挂到parentB的下面,还是将parentB挂到parentA的下面:
一种简单的方式处理方式为:将集合元素个数小的根节点,挂到集合元素个数大的根节点下面
因此需要用一个size数组维护以每个节点为根节点的集合的元素个数
新的union代码如下:
public void union(int a,int b){
int parentA = find(a);
int parentB = find(b);
if (parentA != parentB) {
if (size[parentA] <= size[parentB]) {
p[parentA] = parentB;
size[parentB] += size[parentA];
} else {
p[parentB] = parentA;
size[parentA] += size[parentB];
}
}
}
路径压缩
要降低树的高度,也可以在find操作时进行
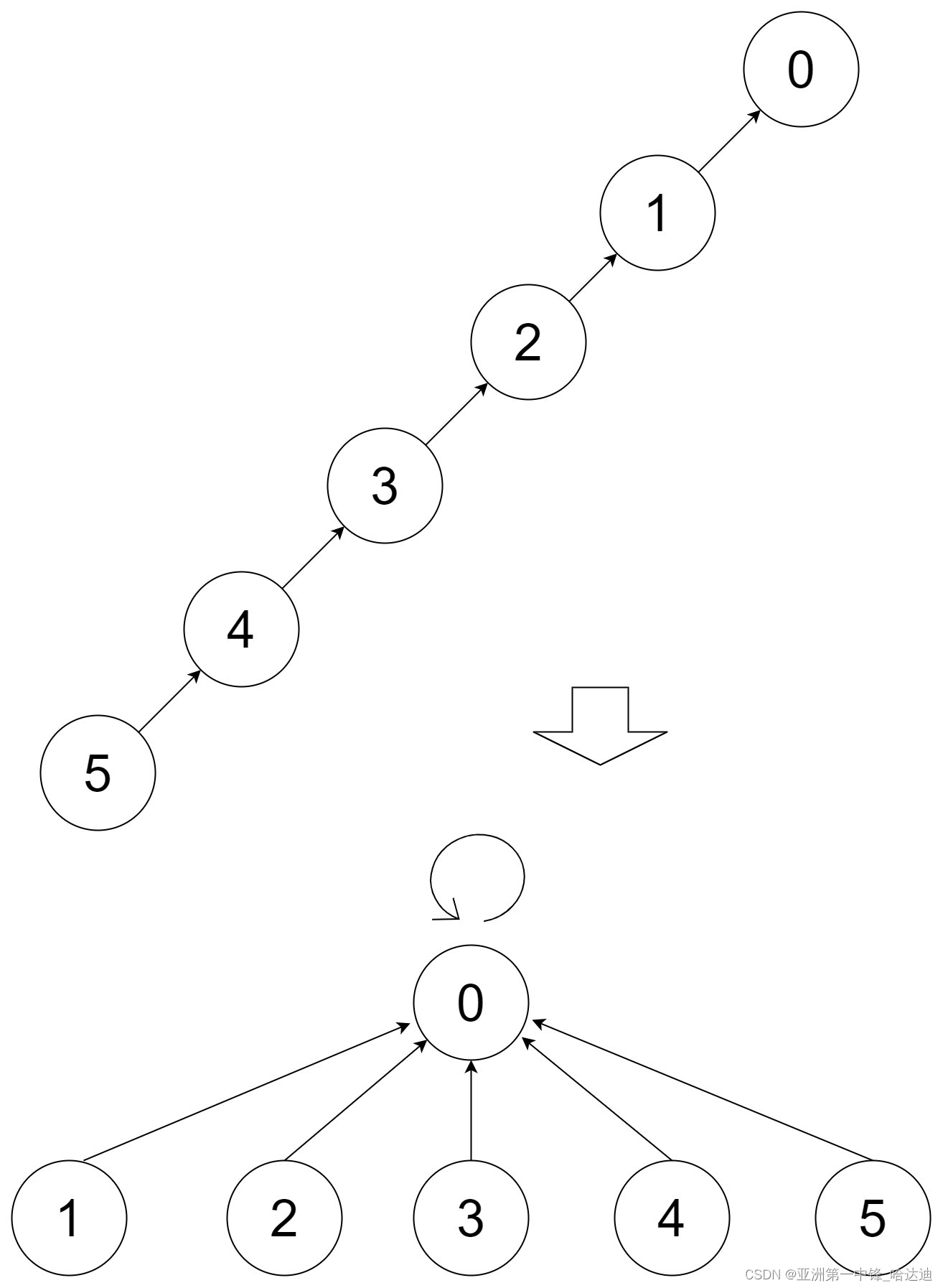
每棵树最理想的情况为,根节点在第一层,其他所有的节点都在第二层,这样后续在这棵树上执行find的时间复杂度为O(1):

在find操作寻找根节点的过程中,可以顺便将树的高度降低,将树变为上图中最理想的情况
怎么做呢?
- 在不断往上找根节点的过程中,
将沿途的所有节点记录到一个栈中 - 找到根节点后,
将栈中所有节点的parent修改为根节点
代码如下:
public int find(int v) {
Stack<Integer> stack = new Stack<>();
stack.push(v);
while (v != p[v]) {
v = p[v];
// 将这条路径上的节点都记录一个栈中
stack.push(v);
}
// 此时v为头结点
// 路径压缩,将这一条路径上所有节点的父都改为cur
while (!stack.isEmpty()) {
p[stack.pop()] = v;
}
return v;
}
完整代码
class UF {
int[] p;
int[] size;
int setSize;
public UF(int cap){
p = new int[cap];
for (int i = 0;i<cap;i++){
p[i] = i;
}
setSize = cap;
}
public int getSetSize() {
return setSize;
}
public int find(int v) {
Stack<Integer> stack = new Stack<>();
stack.push(v);
while (v != p[v]) {
v = p[v];
// 将这条路径上的节点都记录一个栈中
stack.push(v);
}
// 此时v为头结点
// 路径压缩,将这一条路径上所有节点的父都改为cur
while (!stack.isEmpty()) {
p[stack.pop()] = v;
}
return v;
}
public void union(int a,int b){
int parentA = find(a);
int parentB = find(b);
if (parentA != parentB) {
if (size[parentA] <= size[parentB]) {
p[parentA] = parentB;
size[parentB] += size[parentA];
} else {
p[parentB] = parentA;
size[parentA] += size[parentB];
}
}
setSize--;
}
public boolean isConnected(int a,int b) {
return find(a) == find(b);
}
}