
目录
1、Map 和 Set 的概念
2、模型
3、Map 的学习
3.1 关于 Map.Entry
3.2 Map 的常用方法
4、Set 的常用方法
5、 Map 和 Set 的注意点
1、Map 和 Set 的概念
Java 提供了 Map 和 Set 的接口,是一种专门用来进行搜索的容器或数据结构,而他搜索的效率与其具体实例化的子类有关,比如 TreeMap 和 HashMap 的搜索效率就不一样。
如果利用学习到现在的知识,我们要去找一个元素,可能会采取遍历这样的方式,那么时间复杂度是 O(n),也可也采取二分查找,时间复杂度能达到 O(logn), 但必须要求数据是有序的。
如上所说的比较适合静态的查找,也就是一般不会对里面的元素进行插入和删除操作了。
那么假设我要根据学生的学号,找出对应的姓名,或者我要根据学生这样的一个对象,找出他对应的学校相关信息,再或者通讯录中,根据姓名,找出电话。
这些例子是生活中经常会碰到的,也就是在查找时,会更新里面的数据,比如这个学生退学了,就删除掉,即动态查找,那么上述遍历呀,二分查找呀,就不合适了,而 Map 和 Set 是一种适合动态查找的集合容器。
2、模型
通俗来讲,你去吃火锅,有俩宫格的,和单宫格的,甚至多宫格的,那么放在编程里,一般把需要搜索的数据称为关键字 key,和关键字对应的称为值 value,将它称为 Key-value 的键值对,所以模型会有两种:
Key-value 模型:
- 比如有个XX火锅vip客户表,上面对应每个vip客户来消费的次数,即 <vip客户,消费次数>
- 比如每个身份证所对应的人,即 <身份证,人>
纯 Key 模型:
- 比如老师上网课,会议中出现了一个叫 篮球哥 的人,于是让班长看下这个班级中有没有篮球哥这个人。
- 比如当你情敌发了个动态,你会看看你女神有没有给他点赞。
通过两个模型例子来看啊,键值对,也就是说大部分是对应关系,而纯 key 模型,大部分在找是否存在这个key,具体我们后面再细说。
而 Map 存储就是 Key-value 的键值对,Set 只存储了 Key
3、Map 的学习
3.1 关于 Map.Entry<K,V>
Map.Entry<K,V> 是 Map 内部实现用的来存放 <key,value> 键值对的内部类,可以理解成我们之前模拟实现链表时候里面的 Node 节点,也是一个内部类。
这个内部类中,主要提供了 <key,value> 的获取方法和 value 的设置:
| 方法 | 解释 |
|---|---|
| K getKey() | 返回当前 Entry<K,V> 对象中的 key |
| V getValue() | 返回当前 Entry<K,V> 对象中的 value |
| V setValue(V value) | 将键值对中的 value 进行替换指定的 value |
注意:Entry<K,V> 并没有提供 key 的设置,key 的值一定是唯一的,不能重复!
3.2 Map 的常用方法
| 方法 | 解释 |
|---|---|
| V get(Object key) | 返回 key 对应的 value |
| V getOrDefault(Object key, V defaultValue) | 返回 key 对应的 value,key 不存在,返回默认值 |
| V put(K key, V value) | 设置 key 对应的 value |
| V remove(Object key) | 删除 key 对应的映射关系 |
| Set keySet() | 返回所有 key 的不重复集合 |
| Collection values() | 返回所有 value 的可重复集合 |
| Set> entrySet() | 返回所有的 key-value 映射关系 |
| boolean containsKey(Object key) | 判断是否包含 key |
| boolean containsValue(Object value) | 判断是否包含 value |
4、Set 的常用方法
| 方法 | 解释 |
|---|---|
| boolean add(E e) | 添加元素,但重复元素不会被添加成功 |
| void clear() | 清空集合 |
| boolean contains(Object o) | 判断 o 是否在集合中 |
| Iterator iterator() | 返回迭代器 |
| boolean remove(Object o) | 删除集合中的 o |
| int size() | 返回set中元素的个数 |
| boolean isEmpty() | 检测set是否为空,空返回true,否则返回false |
| Object[] toArray() | 将set中的元素转换为数组返回 |
| boolean containsAll(Collection c) | 集合c中的元素是否在set中全部存在,是返回true,否则返回 false |
| boolean addAll(Collection c) | 将集合c中的元素添加到set中,可以达到去重的效果 |
5、 Map 和 Set 的注意点
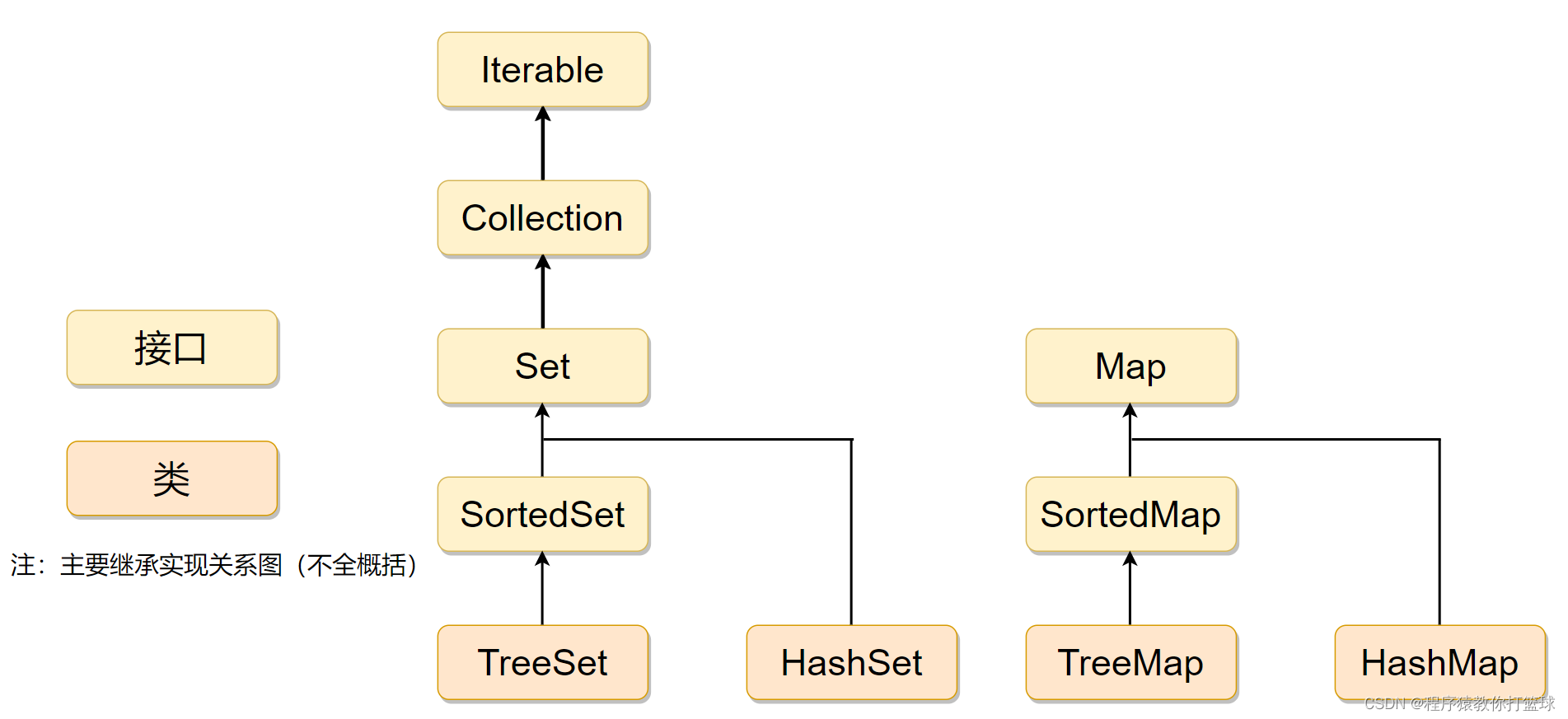
Set 的底层是 Map 来实现的, 讲到后续会体现出来。
Map 没有继承 Iterator 所以不能返回迭代器,而 Set 继承了 Iterator 可以采用迭代器遍历:
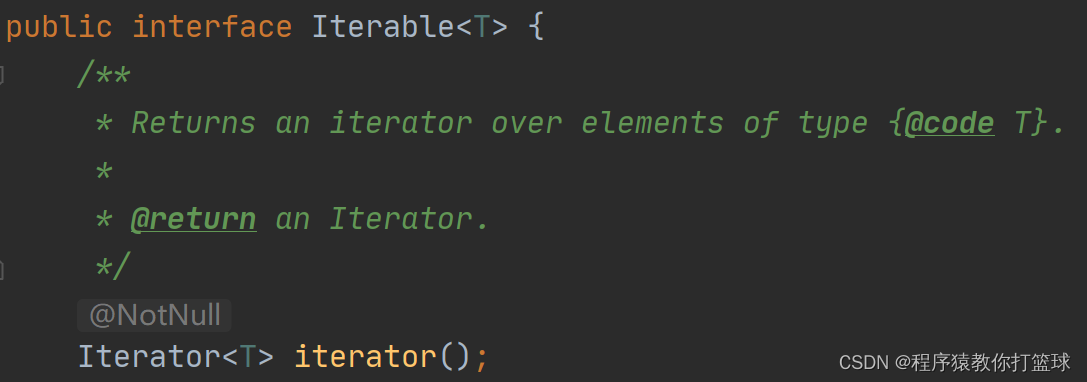
Map 并没有继承 Collection,里面的 key 不能重复,而 Set 虽然继承了 Collection 但是底层实现还是 Map 所以 Set 中的 key 也不能重复。
HashSet 的基础上维护了一个双向链表来记实现Set接口的常用类有 TreeSet 和 HashSet,还有一个LinkedHashSet,LinkedHashSet是在录元素的插入次序。
到这里先了解这么多,具体在后续的 TreeMap,TreeSet,HashMap,HashSet 会体现。
下期预告:【Java 数据结构】TreeMap 和 TreeSet














![比特位计数[动态规划 || bitCount计数]](https://img-blog.csdnimg.cn/726b280349664609b0e96bb52ae66398.png)