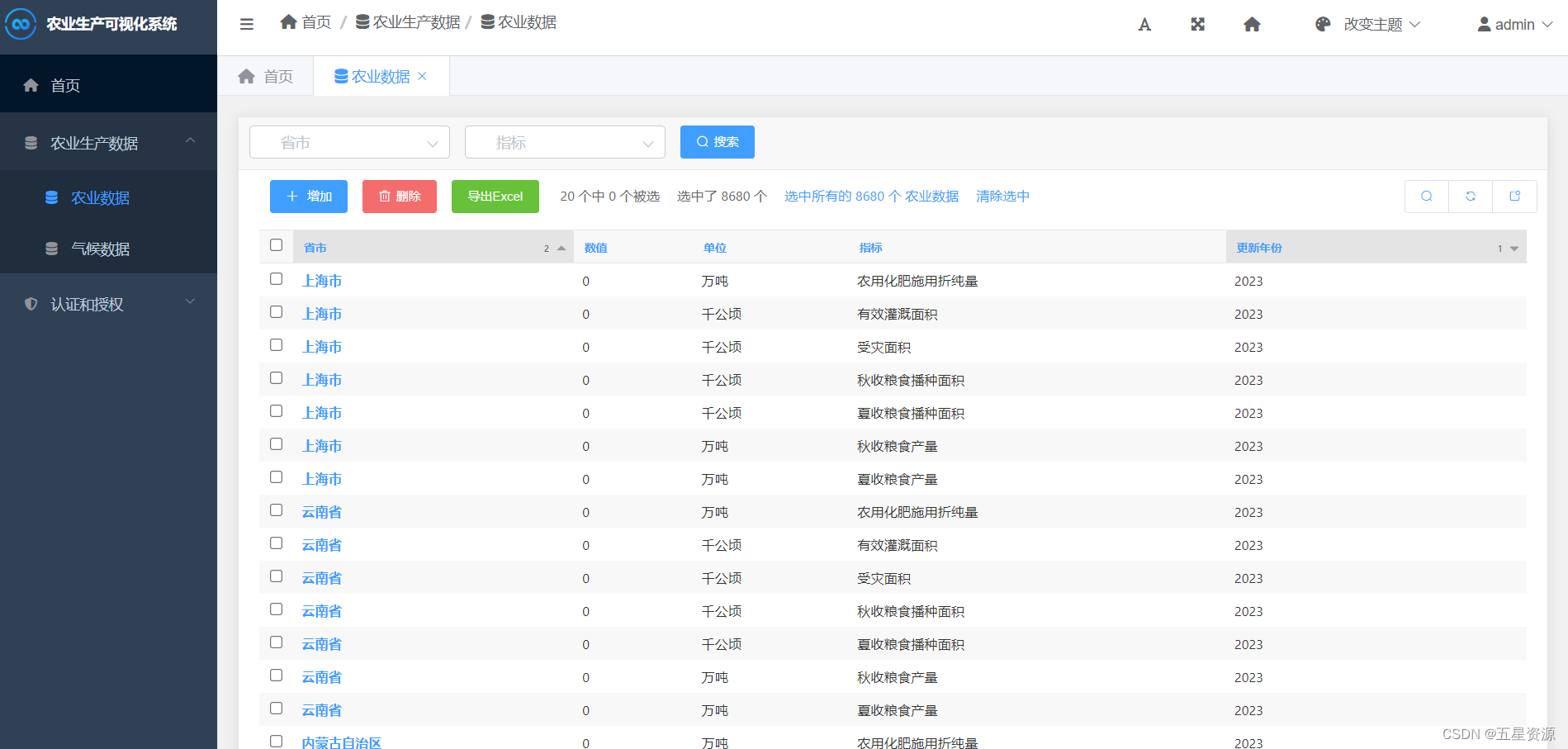
这两天一直在琢磨如下矩阵计算问题。
已知d×m矩阵X和h×q矩阵Y,求如下矩阵:
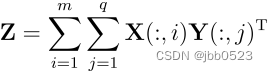
其中X(:,i), Y(:,j)分别表示矩阵X, Y的第i列和第j列,易知Z为d×h矩阵。
如果直接串行计算矩阵Z,两个循环共有m×q,则会很慢,能不能并行化呢?
实际上是可以的,为便于理解,我们先把Z写成如下形式:
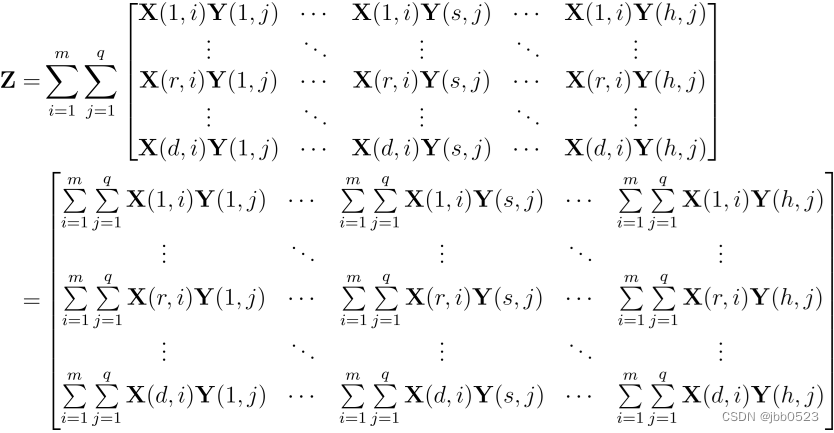
对于矩阵Z中的第(r,s)个元素:
.
注意到第一个括号是X的第r行之和,第二个括号是Y的第s行之和。
也就是说,矩阵Z中的第(r,s)个元素等于X的第r行之和乘以Y的第s行之和。因此,可以先分别将X和Y所有列对应相加,得到长为d的列向量Xsum和长为h的列向量Ysum,则Z等于Xsum乘以Ysum的转置。实际上,推导可以不用这么麻烦,对于目标计算式:

注意到第一个括号是将X所有列对应相加,第二个括号是将Y所有列对应相加,因此Z也就是前面提到的Xsum乘以Ysum的转置。
Matlab代码如下:
function [ Z ] = Mtx_Col_Multi( X, Y )
% Mtx_Col_Multi returns Z = \sum_{i=1}^{m}\sum_{j=1}^{q} X(:,i)*Y(:,j)'
% Here, X(:,i) and Y(:,j) denote the i-th and j-th column of X and Y, respectively
% INPUT:
% X - A dxm matrix
% Y - A hxq matrix
% OUTPUT:
% Z - A dxh matrix
X_sum = sum(X,2);
Y_sum = sum(Y,2);
Z = X_sum*Y_sum';%dxh
% %This function implements the following procedure in parallel
% Z = zeros(d,h);%dxh
% for ii=1:m
% x_i = X(:,ii);
% for jj=1:q
% y_j = Y(:,jj)';
% Z = Z + x_i*y_j;
% end
% end
end其实我真正想计算的是如下运算,里面包含一个系数:

其中C(i,j)是一个系数,是矩阵C中的第(i,j)个元素。那么这个运算能不能并行化呢?
使用类似的思想:
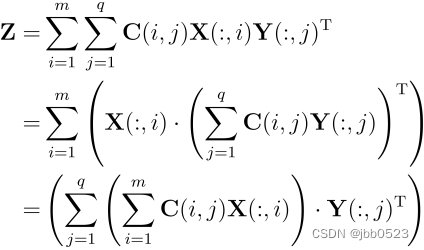
因此,可以编写如下函数:
function [ Z ] = Mtx_Coef_Col_Multi( X, Y, C )
% Mtx_Coef_Col_Multi returns Z = \sum_{i=1}^{m}\sum_{j=1}^{q} C(i,j)*X(:,i)*Y(:,j)'
% Here, X(:,i) and Y(:,j) denote the i-th and j-th column of X and Y, respectively
% C(i,j) denotes the item in i-th row and j-th column of C.
% INPUT:
% X - A dxm matrix
% Y - A hxq matrix
% C - A mxq matrix
% OUTPUT:
% Z - A dxh matrix
d = size(X,1);
h = size(Y,1);
[m,q] = size(C);
if q<m
Z = zeros(d,h);%dxh
for jj=1:q
y_j = Y(:,jj)';%1xh
c_j = C(:,jj)';%1xm
X_c = bsxfun(@times, X, c_j);%dxm
X_sum = sum(X_c,2);%dx1
Z = Z + X_sum*y_j;%dxh
end
else
Z = zeros(d,h);%dxh
for ii=1:m
x_i = X(:,ii);%dx1
c_i = C(ii,:);%1xq
Y_c = bsxfun(@times, Y, c_i);%hxq
Y_sum = sum(Y_c,2);%hx1
Z = Z + x_i*Y_sum';%dxh
end
end
% %This function implements the following procedure in parallel
% Z = zeros(d,h);%dxh
% for ii=1:m
% x_i = X(:,ii);
% for jj=1:q
% y_j = Y(:,jj)';
% Z = Z + C(ii,jj)*x_i*y_j;
% end
% end
end可以使用如下代码测试一下上述并行化实现方法与串行实现的效率差异:
%demo for Mtx_Coef_Col_Multi
clc;clear;close;
d = 5;
m = 10000;
h = 8;
q = 50;
X = rand(d,m);
Y = rand(h,q);
C = rand(m,q);
tic;
Z_serial = zeros(d,h);%dxh
for ii=1:m
x_i = X(:,ii);
for jj=1:q
y_j = Y(:,jj)';
Z_serial = Z_serial + C(ii,jj)*x_i*y_j;
end
end
toc;
tic;
Z = Mtx_Coef_Col_Multi(X, Y, C);
toc;
norm(Z_serial-Z,'fro')命令行窗口输出如下信息(有一定的随机性,每次运行结果有些差异):
时间已过 1.011418 秒。
时间已过 0.009981 秒。
ans =
6.5505e-09
也就是在当前设置下,并行实现版本的效率提交了100倍左右。