引言

今天把所有的最短路算法和最小生成树算法又给复习了一下，有 $spfa,朴素版dijkstra,堆优化版dijkstra,floyd,prim,kruskal$ 这些算法全部都给写了个一遍，感觉还是很多都是很像的，比如说 $朴素版dijkstra和prim$ 简直是非常的相像，并且自我感觉这些算法已经很熟了，因为我最开始写模板就是写最短路算法的，估计已经写了快七八十遍了，但是今天写的时候还是感觉有点不太熟悉，可能是这几周各种比赛和事都比较多，也很迷茫所以状态也没有之前的那么好，心里总是静不下来，还是放松了，干啥都不在状态，所以感觉在下降，所以得继续静下心来，好好地学新的东西了，加油！

---

一、滑动窗口

标签：单调队列、模板题

思路：就是维护一个长度小于等于 $k$ 的一个单调队列，以找窗口的最小值为例。我们要做的就是保证这个窗口里的元素是单调递增的，然后最小值就是队头的元素。首先进行一个操作的时候我们要确保该窗口的大小是小于等于 $k$ 的，即队头不能出这个窗口，因为当窗口移动到第 $i$ 号元素的时候，我们的队头要确保 $q[hh]\ge i-k+1$ ，然后再进行维护该队列是一个单调递增的，所以因为当前队列里的元素是单调递增的，所以我们得从队尾和第 $i$ 号元素进行比较，如果队尾大于等于该元素，那么就出队。如下图所示，如果该窗口里的元素为 $3,-1,-3$ ，那么 $3$ 就没有存在的必要了，因为总有 $-3\le 3$ ，并且 $-3$ 比 $3$ 活得时间还长，$-1$ 也是同理，所以这样自然而然整个队列就是一个严格单调递增的队列了，所以每次维护这个队列，并且当满足 $k$ 个元素时，输出队头元素即可，输出最大值同理。

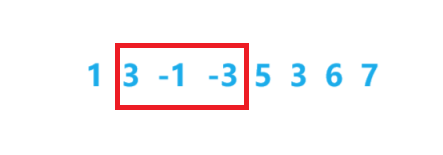
题目描述：

给定一个大小为 n≤106 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式
输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式
输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：
8 3
1 3 -1 -3 5 3 6 7
输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 1e6+10;

int n, k;
int a[N], q[N];

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	cin >> n >> k;
	for(int i = 0; i < n; ++i) cin >> a[i];
	
	int hh = 0, tt = -1;
	for(int i = 0; i < n; ++i)
	{
		if(hh <= tt && q[hh] < i - k + 1) hh++;
		while(hh <= tt && a[i] <= a[q[tt]]) tt--;
		
		q[++tt] = i;
		if(i >= k - 1) cout << a[q[hh]] << " ";
	}
	cout << endl;
	
	hh = 0, tt = -1;
	for(int i = 0; i < n; ++i)
	{
		if(hh <= tt && q[hh] < i - k + 1) hh++;
		while(hh <= tt && a[i] >= a[q[tt]]) tt--;
		
		q[++tt] = i;
		if(i >= k - 1) cout << a[q[hh]] << " ";
	}
	cout << endl;
	
	return 0;
}

---

二、单调栈

标签：单调栈、模板题

思路：在一个序列中，求每一个数的左边或者右边第一个比它小或者大的数，就可以用单调栈来求，以这道题为例，求每个数左边第一个比它小的数，那么这个单调栈里面存的是一个严格上升的序列，首先取栈顶判断是否比它小，如果比它大那么出栈顶继续判断，因为只要有当前元素存在，这些出栈的元素就不会用到，所以栈里面存的就是有用且最简的元素，在里面找就行了，最后输出，然后入栈当前元素。

题目描述：

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式
第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式
共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围
1≤N≤105

1≤数列中元素≤109
输入样例：
5
3 4 2 7 5
输出样例：
-1 3 -1 2 2

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 1e5+10;

int n;
int stk[N];

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	cin >> n;
	
	int tt = 0;
	while(n--)
	{
		int x; cin >> x;
		while(tt && stk[tt] >= x) tt--;
		if(tt) cout << stk[tt] << " ";
		else cout << -1 << " ";
		
		stk[++tt] = x;
	}
	
	return 0;
}

---

三、繁忙的都市

标签：最小生成树

思路：其实就是一个 $prim$ 算法，看题目没有说无解，所以第一问肯定是 $n-1$ ，然后第二问就是在求生成的最小生成树里的边找一个最大的就行了，没什么难的。只要这个算法不是死记硬背的，真的理解了，其实就是很小的改动而已。

题目描述：

城市C是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。

城市C的道路是这样分布的：

城市中有 n 个交叉路口，编号是 1∼n，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。

这些道路是 双向 的，且把所有的交叉路口直接或间接的连接起来了。

每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。

但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

1．改造的那些道路能够把所有的交叉路口直接或间接的连通起来。

2．在满足要求1的情况下，改造的道路尽量少。

3．在满足要求1、2的情况下，改造的那些道路中分值最大值尽量小。

作为市规划局的你，应当作出最佳的决策，选择哪些道路应当被修建。

输入格式
第一行有两个整数 n,m 表示城市有 n 个交叉路口，m 条道路。

接下来 m 行是对每条道路的描述，每行包含三个整数u,v,c 表示交叉路口 u 和 v 之间有道路相连，分值为 c。

输出格式
两个整数 s,max，表示你选出了几条道路，分值最大的那条道路的分值是多少。

数据范围
1≤n≤300,1≤m≤8000,1≤c≤10000
输入样例：
4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8
输出样例：
3 6

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 310;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int prim()
{
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;
	
	int maxv = 0, cnt = 0;
	for(int i = 0; i < n; ++i)
	{
		int t = -1;
		for(int j = 1; j <= n; ++j)
		{
			if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
		}
		
		if(i) maxv = max(maxv, dist[t]);
		st[t] = true;
		
		for(int j = 1; j <= n; ++j) dist[j] = min(dist[j], g[t][j]);
	}
	
	return maxv;
}

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	memset(g, 0x3f, sizeof g);
	cin >> n >> m;
	while(m--)
	{
		int a, b, c; cin >> a >> b >> c;
		g[a][b] = g[b][a] = min(g[a][b], c);
	}
	
	int t = prim();
	cout << n - 1 << " " << t << endl;
	
	return 0;
}