一. 题目链接 

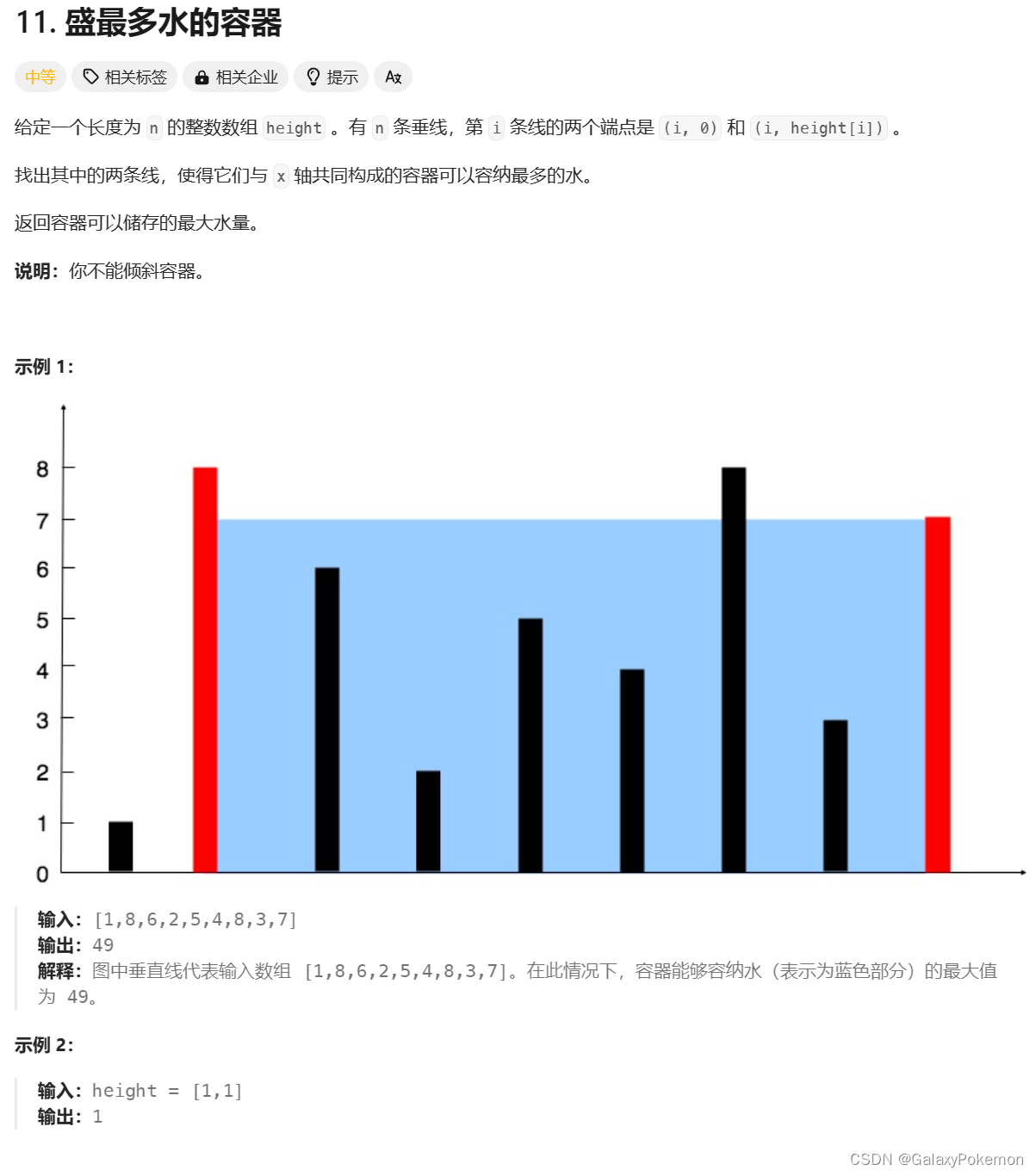
LeetCode - 11.盛最多水的容器

二. 思路解释

利用双指针的思想，定义一个left和reght，left指向首部，right指向尾部，计算当前两个指针所对应的高度构成容器的体积。根据当前双指针所指的高度的大小，然后让指针向内移动，直到left=right（一开始left指向首部，right指向尾部，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，在这种情况下想要让容器盛水变多，就只有在容器的高上下功夫。 那我们该如何决策哪个指针移动呢？我们能够发现不管是左指针向右移动一位，还是右指针向左移动一位，容器的底都是一样的，都比原来减少了 1。这种情况下我们想要让指针移动后的容器面积增大，就要使移动后的容器的高尽量大，所以我们选择指针所指的高较小的那个指针进行移动，这样做可以保留较高柱子的边界，同时增加找到更高柱子并提升容器高度的可能性）

1. 初始化指针： 设置两个指针，一个在数组的开始位置（称为left），另一个在数组的结束位置（称为right）。

2. 计算容积： 容器的容积由两个指针指向的柱子中较短的那一个决定（因为水的高度由较短的柱子决定），以及两个柱子之间的距离。容积的计算公式为：(right - left) * min(height[left], height[right])。

3. 移动指针： 比较两个指针指向的柱子的高度：

   • 如果height[left] < height[right]，则移动left指针向右移动（即left++），因为在这种情况下，可能存在一个更高的柱子在左指针的右边，能与右指针形成更大容积的容器。
   • 反之，如果height[right] <= height[left]，则移动right指针向左移动（即right--），出于同样的逻辑，可能存在一个更高的柱子在右指针的左边。

4. 重复计算与移动： 持续进行容积的计算，并根据上述逻辑移动指针，直到left和right相遇。

5. 输出最大容积： 在整个过程中，保持一个变量来记录遇到的最大容积，最后输出这个最大值。

使用双指针方法的优点是时间复杂度为O(n)，比暴力解法的O(n^2)要高效得多。这种方法之所以有效，是因为它利用了柱子之间距离的递减和可能遇到更高柱子的机会来逐步缩小搜索范围，同时保证没有错过可能的最大容积配置。

• 时间复杂度 O(N)
• 空间复杂度 O(1)

三. 动画解释

四. 代码解释

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;//初始化左指针
        int right = height.size() - 1;//初始化右指针
        int res = 0;  // 初始化结果变量

        while (left < right) {
            int currentArea = (right - left) * min(height[left], height[right]);//计算当前的面积
            res = max(res, currentArea);  // 更新最大面积

            if (height[left] > height[right]) {
                right--;  // 移动较短的一边
            } else {
                left++;  // 移动较短的一边
            }
        }
        return res;
    }
};

注意：每次进行完计算res体积之后，要和之前的res进行对比，如果比它大就替换，比它小就不替换