最近在调研符号执行工具优化方式时，发现好几篇工作都用到了动态程序切片，以前大部分接触的都是静态切片，对动态切片几乎不了解。所以开始学习动态切片，我主要参考的是90年的一篇上古paper。

1.静态依赖图和静态切片

说到程序切片，就离不开程序依赖图这个概念，我之前写了一篇blog介绍静态程序依赖图，这里再简单提一下。

在程序依赖图中：

每个结点表示一个语句（statement，与之相对的是块语句-compound statement）或者指令（read, write, assignment）。
边包括控制依赖边和数据依赖边（paper中给出的依赖方向和我平时应用的相反，这里按照paper中的来）
- 数据依赖边 $v_i \rightarrow v_j$ ，意味着语句 $v_i$ 使用了变量 var，是在语句 $v_j$ 中定义的。并且从 $v_j$ 到 $v_i$ 的路径上 var 没有重新被定义。
- 控制依赖边 $v_i \rightarrow v_j$ 表示 $v_i$ 是否被执行取决于条件表达式 $v_j$ 的值。

以下面程序为例

示例1

x = read(); // S1
if (x < 0) { // S2
    y = f1(x); // S3
    z = g1(x); // S4
}
else {
    if (x == 0) { // S5
        y = f2(x); // S6
        z = g2(x); // S7
    }
    else { 
        y = f3(x); // S8
        z = g3(x); // S9
    }
}
write(y); // S10
write(z); // S11

静态依赖图如下（标注了 CD 的是控制依赖边）：

在静态依赖图中，在 S10 关于变量 y 的reaching-definition包括了 S3, S6, S8，在整个依赖图上进行切片，可以得到slice为 {1, 2, 3, 5, 6, 8}。

2.动态切片

上面示例中的程序，S3, S6, S8 都会对 y 赋值，对于任意输入 x，3条语句只有1个会执行。所以动态切片指挥保留1个。

如果输入 x = -1，那么最终的动态slice为 {1, 2, 3}，显然动态slice比静态slice要更精简，更容易定位bug。

下面部分我就给出paper中提到的4种进行动态切片的算法，首先给出execution history（执行历史）的概念。

execution history是一个在给定testcase下的语句序列 ${v_1, ..., v_n\}$ ，序列按照执行顺序排序好。如果同一个语句在execution history中出现多次，那么会用上标表示，比如下面示例：

示例2

n = read(); // S1
z = 0; // S2
y = 0; // S3
i = 1; // S4
while (i <= n) { // S5
    z = f1(z, y); // S6
    y = f2(y); // S7
    i = i + 1; // S8
}
write(z); // S9

依赖图为

上面示例当输入 n = 2 时，execution history为 ${1, 2, 3, 4, 5^1, 6^1, 7^1, 8^1, 5^2, 6^2, 7^2, 8^2, 5^3, 9\}$ 。

给定程序 P 的execution history hist，testcase test，变量 var。关于 var 的动态slice是 hist 中执行结果对 var 有影响的结点集合。简单的说，动态slice仅关注 hist 中的语句而不是整个程序 P 中的。

2.1.方法1

在第一个示例中 S10 中 y 的值受 S3, S6, S8 影响。但这3个语句一次只可能执行1个。那么在静态依赖图中标注出当前testcase执行过的语句，并且切片时只遍历标注的结点。那么就可以获得当前testcase的动态切片。

跟纯静态切片相比，这种方法多出的步骤就是标记执行过的语句，并且切片时只遍历标记过的语句。

以第一个示例为例，输入 x = -1。execution history为 1, 2, 3, 4, 10, 11。所以对于变量 y slice出的结果是 1, 2, 3。

但是这种朴素的方法也不是总会产生精准的动态切片，它有时候会引入额外的结点（过拟合）。示例2中当输入 n = 1 时，execution history为 ${1, 2, 3, 4, 5^1, 6, 7, 8, 5^2, 9\}$ ，此时关于变量 z 产生的动态切片为包含所有结点。但实际上execution history中 $7$ 对 y 进行了赋值而之后再也没使用，所以 S7 不应该出现在动态切片中。

可以看到上面的问题是在循环语句中引入的，那么从静态slice -> 方法1，由分支语句引起的依赖过拟合问题已得到缓解。

2.2.方法2

方法2可以看作方法1的改进。方法1的问题在于，一个语句可能在程序流图中具有同一变量的多个到达定义（Reaching-Definition），但同一时刻只有1个会影响其变量值。

在示例2中， S6 关于变量 y 依赖于 S3 和 S7，关于变量 z 依赖于 S2 和 S6。当 n = 1 时，这4个依赖语句都被执行了，但是 S6 --> S7 之间的依赖关系并没有被触发，方法1错误的包含了这种依赖关系。

方法2的思路就是标记边（方法1是标记结点），在程序执行的过程中如果一条依赖边边被触发了，那么标记该依赖边。切片时只遍历标记过的依赖边。

以示例2为例，输入 n = 1 时，依赖边 S6 --> S7 和 S9 --> S2 没有被标记，那么最终动态切片为 {1, 2, 3, 4, 5, 6, 8}（没有7）。

当没有循环出现的时候，上面的方法能找到准确的动态切片。但是有时候，方法2依旧会引入一些不必要的语句。以下面示例为例

示例3

n = read(); // S1
i = 1; // S2
while (i <= n) { // S3
    x = read(); // S4
    if (x < 0) // S5
        y = f1(x); // S6
    else
        y = f2(x); // S7
    z = f3(y); // S8
    write(z); // S9
    i = i + 1; // S10
}

当输入 n = 2，2次输入 x 分别为 -4, 3 时。execution history为 ${1, 2, 3^1, 4^1, 5^1, 6, 8^1, 9^1, 10^1, 3^2, 4^2, 5^2, 7, 8^2, 9^2\}$ ，在第2轮， $9^2 \rightarrow 7$ ，在第1轮， $9^1 \rightarrow 6$ 。当要对变量 z 进行动态切片时，采用方法2会将 S6, S7 都包括进来，而实际上只需要 S7 就够了。因为第2轮 $9^2 \rightarrow 7$ 。

一种朴素的解决方案在标记一个语句的依赖关系前取消其已有的标记（unmark），这种方案对示例3是管用的，但是依旧可能会造成错误的切片，以下面示例为例

示例4

n = read(); // S1
a = 0; // S2
i = 1; // S3
while (i <= n) { // S4
    x = read(); // S5
    if (x < 0) // S6
        y = f1(x); // S7
    else
        y = f2(x); // S8
    z = f3(y); // S9
    if (z > 0) // S10
        a = f4(a, z); // S11
    i = i + 1; // S12
}
write(a); // S13

循环执行了2次，第一次执行了 S7 和 S11，第二次执行了 S8 跳过了 S11，那么在结尾对 a 进行切片时，slice中出现的是 S8 而不是 S7。根源在于 S7 --> S9 的依赖关系被 S8 --> S9 取代了，而 a 依赖的是第一次循环的结果。

2.3.方法3

方法2中因为循环的问题，1个语句可能在execution history中出现多次，每次可能会依赖不同的语句，从而导致过拟合。这就催生出了第3种方法：

对于execution history中的语句，如果出现多次，那么每一次都在动态依赖图上创建一个不同的结点，它们只依赖于当前对它们有影响的结点。在这种情况下，每一个结点针对一个变量只会依赖于一个结点。

以示例3为例，输入 n = 3，3次 x 取值分别为 -4, 3, 2， execution history为 ${1, 2, 3^1, 4^1, 5^1, 6^1, 8^1, 9^1, 10^1, 3^2, 4^2, 5^2, 7, 8^2, 9^2, 10^2, 3^3, 4^3, 5^3, 6^2, 8^3, 9^3, 10^3, 3^4\}$

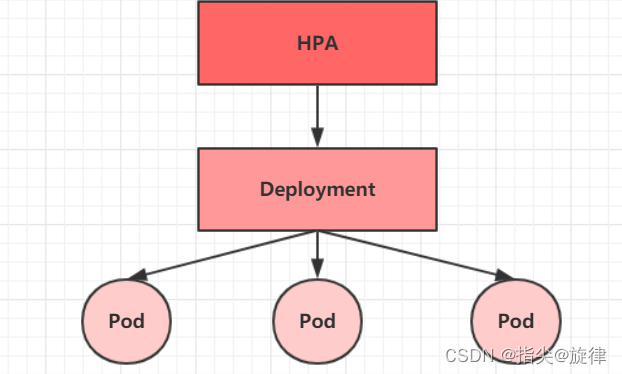
依赖图如下图所示，同一条语句循环n次就会创建n个结点，每次的依赖关系可能不同，对同一个变量只会依赖1个结点。图中粗体显示的为对 write(z); 进行slice得到的结点集合。

在这里插入图片描述

2.4.方法4

方法3中动态依赖图的大小（节点和边的总数）通常是无限的。这是因为图中的节点数等于execution history中的语句数而非代码的语句数，而这通常取决于运行时输入的值。而同时，每个程序只能有有限数量的可能动态切片——每个切片都是（有限）程序的子集。

这表明限制动态依赖图中的节点数量是可行的。第4个方法便是利用这个insight：不要为execution history中的每一个语句创建一个新节点，而是仅当具有相同传递依赖关系的另一个节点不存在时才创建一个节点。

基于上述方法创建出来的依赖图叫Reduced Dynamic Dependence Graph（简化动态依赖图，RDDG）。为了创建RDDG，执行时需要创建2个表 DefnNode, PredNode：

DefnNode 将1个变量名映射到上次赋值到这个变量中的依赖图结点，在C++中可通过 map 实现，在python中通过 dict 实现。
PredNode 将1个control predicate statement（条件判断语句，基本上就是 if, while 条件）映射为该predicate在execution history中的最后一次出现相对应的结点。

此外，依赖图中每一个结点，都会包含1个 set 型成员变量：ReachableStmts，包含该结点依赖路径上的全部语句（是语句不是结点，不区分第几次执行）。算法执行过程包括：

1.每当一个语句 $S_i$ 被执行，算法会计算由最近一次对 $S_i$ 引用的变量赋值的结点组成的集合 $D$ 。以及由 $S_i$ 控制依赖的结点（结点对应条件判断在execution history中最近一次出现）组成的集合 $C$ 。
2.如果 $S_i$
- 2.1.之前已经执行过并且对应的结点是 $n$ ，其直接后代与 $\cup C$ 相同，则 $S_i$ 这次执行对应的结点依旧是 $n$ 。
- 2.2.否则，为 $S_i$ 创建一个新的结点 $n^{'}$ ， $n^{'}$ 所有的出边指向 $\cup C$ 中的所有结点。
3.如果 $S_i$ 对一些变量进行了赋值，那么将这些变量在 DefnNode 中的表项更新为 $n^{'}$ 。
4.如果 $S_i$ 是一个control predicate（条件判断），PredNode 中 $S_i$ 对应的表项更新为 $n^{'}$ 。

上述4个步骤在没有环路依赖的情况下可以正常工作，但是程序中存在环路依赖（由循环语句导致的），上述依赖图缩减工作不能正常运行。可以添加下面步骤解决：

对于语句 $S_i$ ，在需要创建结点的时候（2.2）首先确定对应结点 $n^{'}$ 的直接后继结点集合（ $\cup C$ 中的）中的任意一结点，记作 $v$ （ $n^{'}$ 依赖于 $v$ ），是否对 $S_i$ 之前执行对应的结点产生依赖以及 $n^{'}$ 的其它直接后继结点是否从 $v$ 可达。这可以通过检查 $n^{'}$ 的 ReachableStmts 是否是 $v$ 的 ReachableStmts 的子集来实现。
- 如果是，那么将 $n^{'}$ 与 $v$ 合并。

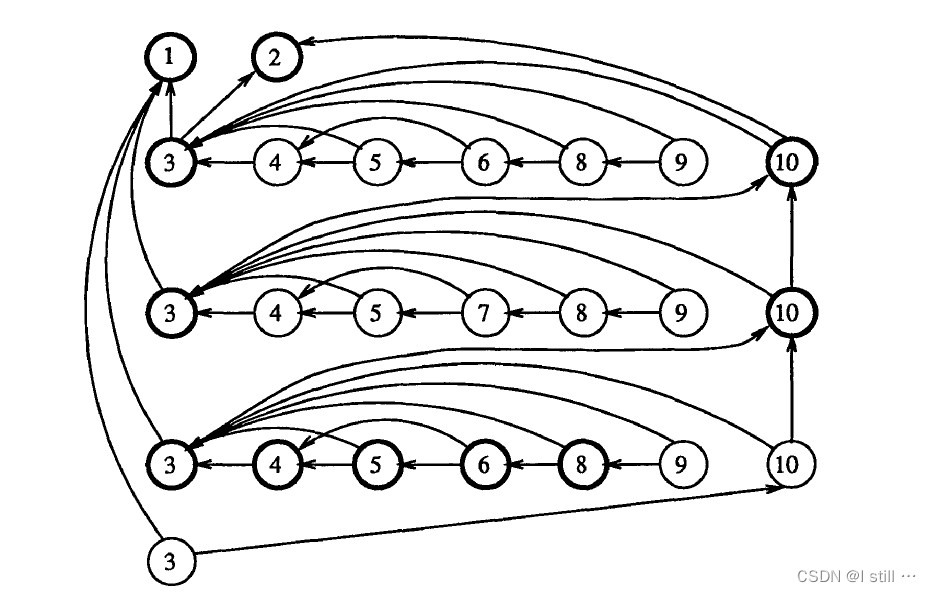
示例3对应的RDDG如下，每个结点都标注了其 ReachableStmts，当 S3 第2次执行时，对应结点 $3^2$ 依赖于 $10$ 。并且 $3^1$ 的 ReachableStmts: {1, 2, 3} 是 $10$ 的 ReachableStmts: {1, 2, 3, 10} 的子集。因此 $3^2$ 并入 $10$ 。

在进行slice时，直接查找结点就能找到slice包含的语句，都不需要遍历RDDG了。

在这里插入图片描述
用方法4分析示例3大致过程如下：

执行代码 n = read();，且该语句并没有依赖任何结点，所以 $\emptyset, C = \empty$ ，该语句此前未执行过，因此创建结点 $n_1$ 。该语句定义了变量 n，DefnNode[n] = n1。
执行代码 i = 1;，跟 S1 一样，没有执行过没有依赖结点，创建依赖图结点 $n_2$ 。定义了变量 i，DefnNode[i] = n2。
执行代码 i <= n，引用了变量 i, n ，上一次赋值分别在 $n_1, n_2$ 结点（查 DefnNode 表），没有控制依赖于其它结点。 $\{n_1, n_2\}, C = \empty$ ，没有执行过，创建结点 $n_3$ 。并且添加 $n_3 \rightarrow n_2, n_3 \rightarrow n_1$ 的数据依赖边。S3 为控制语句，PredNode[S3] = n3。
执行代码 x = read();，对 S3 有控制依赖，上一次执行是在 $n_3$ （查 PredNode 表）。 $\empty, C = \{n_3\}$ ，没有执行过，创建结点 $n_4^1$ 。添加控制依赖边 $n_4^1 \rightarrow n_3$ 。定义了变量 x，DefnNode[x] = n41。
执行代码 x < 0，引用变量 x，上一次赋值是在 $n_4^1$ ；控制依赖于 S3，上一次执行是在 $n_3$ ， $D = \{n_4^1\}, C = \{n_3\}$ ；没有执行过，创建结点 $n_5^1$ 。添加数据依赖边 $n^1_5 \rightarrow n_4^1$ ，控制依赖边 $n^1_5 \rightarrow n_3$ 。为控制语句，PredNode[S5] = n51。
执行代码 y = f1(x);，引用了变量 x，上一次赋值是在 $n_4^1$ ；控制依赖于 S5，上一次执行是在 $n_5^1$ ， $D = \{n_4^1\}, C = \{n_5^1\}$ ；没有执行过，创建结点 $n_6^1$ ；添加数据依赖边 $n^1_6 \rightarrow n_4^1$ ，控制依赖边 $n^1_6 \rightarrow n^1_5$ 。S6 定义了 y，DefnNode[y] = n61。
执行代码 z = f3(y);，引用了变量 y，上一次赋值是在 $n_6^1$ ；控制依赖于 S3，上一次执行是在 $n_3$ ， $D = \{n_6^1\}, C = \{n_3\}$ ；没有执行过，创建结点 $n_8^1$ ；添加数据依赖边 $n^1_8 \rightarrow n_6^1$ ，控制依赖边 $n^1_8 \rightarrow n_3$ 。S8 定义了 z，DefnNode[z] = n81。
执行 write(z); … ,创建 $n_9^1$ ，添加数据依赖边 $n_9^1 \rightarrow n_8^1$ ，控制依赖边 $n_9^1 \rightarrow n_3$ 。
执行 i = i + 1，创建 $n_{10}$ ，添加数据依赖边 $n_{10} \rightarrow n_2$ ，控制依赖边 $n_10 \rightarrow n_3$ 。DefnNode[i] = n10。
再次执行 i <= n，引用变量 i, n，上次赋值分别是在 $n_{10}, n_1$ 。 $\{n_{10}, n_2\}, C = \empty$ ，执行过一次，上次执行结点为 $n_3$ ，但是 $n_3$ 后继为 $n_1, n_2$ 。所以新建结点 $n_3^{'}$ ，应该添加数据依赖边 $n_3^{'} \rightarrow n_{10}, n_3^{'} \rightarrow n_1$ 。但是 $n_3^{'}$ 对应的 ReachableStmts 为 1, 2, 3, 10，跟 $n_{10}$ 相同，算子集，因此 $n_3^{'}$ 并入 $n_{10}$ 。 $n_3^{'} \rightarrow n_1$ 变成 $n_{10} \rightarrow n_1$ 。PredNode[S3] = n10。
再次执行 x = read();，控制依赖于 S3， $\empty, C = \{n_{10}\}$ 。执行过一次但是 $n_4^1$ 的直接后继为 $n_3$ ，与 $\cup C$ 不同。新建 $n_4^2$ ，且不需要合并结点。DefnNode[x] = n42。
再次执行 x < 0，引用 x，控制依赖于 S3， $D = n_4^2, C = n_{10}$ 。执行过一次但是依旧需要新建结点，新建 $n_5^2$ ，不需要合并结点。PredNode[S5] = n52。
执行 y = f2(x);，引用 x，控制依赖于 S5， $D = \{n_4^2\}, C = \{n_5^2\}$ 。没有执行过，新建 $n_7$ 。添加数据依赖边 $n_7 \rightarrow n_4^2$ ，控制依赖边 $n_7 \rightarrow n_5^2$ 。DefnNode[y] = n7。
再次执行 z = f3(x);，新建结点 $n_8^2$ ， $D = \{n_7\}, C = \{n_{10}\}$ 。添加数据依赖边 $n_8^2 \rightarrow n_7$ ，控制依赖边 $n_8^2 \rightarrow n_{10}$ 。DefnNode[z] = n82。
再次执行 write(z)，新建 $n_9^2$ ，添加数据依赖边 $n_9^2 \rightarrow n_8^2$ ，控制依赖边 $n_9^2 \rightarrow n_{10}$ 。
再次执行 i = i + 1，引用 i，控制依赖于 S3， $D = \{n_{10}\}, C = \{n_{10}\}$ 。可以新建结点 $n_{10}^{'}$ ，但是 $n_{10}^{'}$ 和 $n_{10}$ 的 ReachableStmts 相同，因此可以合并2个结点。
第3次执行 i <= n，引用 i, n， $D = \{n_{10}, n_1\}$ 。同样，新建了结点但是又并入 $n_{10}$ 。
第3次执行 x = read();， $\empty, C = \{n_{10}\}$ 。之前执行过对应结点为 $n_4^2$ ，后继为 ${n_{10}\}$ 和 $\cup C$ 相同。因此不新建结点。
第3次执行 x < 0，同理不新建结点。
再次执行 y = f1(x);，引用变量 x，控制依赖于 S5， $D = \{n_4^2\}, C = \{n_5^2\}$ 。执行过对应结点 $n^1_6$ ，后继和 $\cup C$ 不同，新建 $n_6^2$ 。添加数据依赖边 $n_6^2 \rightarrow n_4^2$ ，控制依赖边 $n_6^2 \rightarrow n_5^2$ 。DefnNode[y] = n62。
对于之后2个语句，它们之前执行过但是由于之前对应结点后继和 $\cup C$ ，不同，需要新建结点。
对于最后执行的 i = i + 1，依旧是先新建结点然后合并。