树与二叉树
在之前的学习中,我们一直学习的是一个线性表,数组和链表这两种都是一对一的线性表,而在生活中的更多情况我们要考虑一对多的情况,这时候就引申出了我的新的数据结构那就是树,而树经过一些规矩的指定也就成为了我们的一个二叉树。
树的定义
树是一种非线性的一种数据结构,是一种一对多的数据结构,特点如下:
- 结点之间存在分支关系
- 结点之间存在层次关系
树的基本定义如下:
-
树(Tree)是n(n≥0)个结点的有限集
-
有且仅有一个特定的称为根(Root)的结点
-
n = 0是一个空树
-
当n>1时,其余结点可分为m(m>0)个互不相交的有限集T 1 、T 2 、……、T m ,其中每一个集合本身又是一棵树,并且称为根的子树。
树如下图所示:
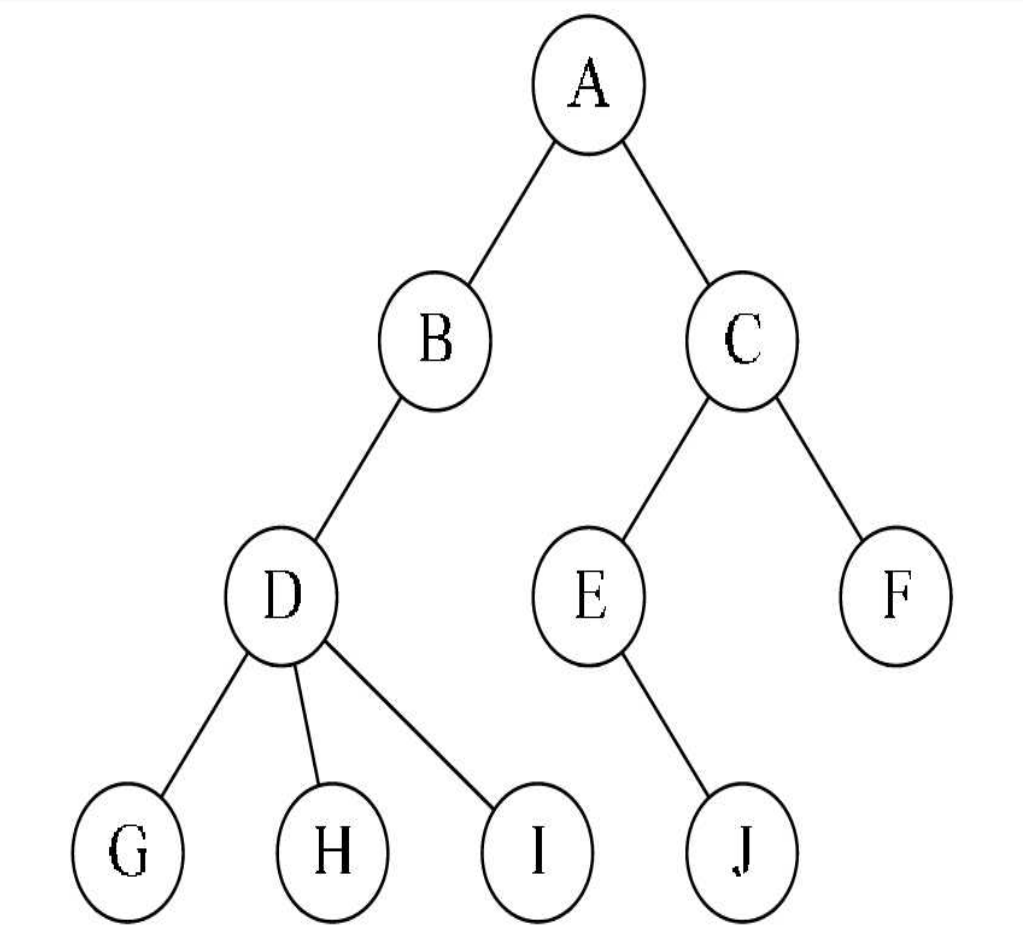
注:
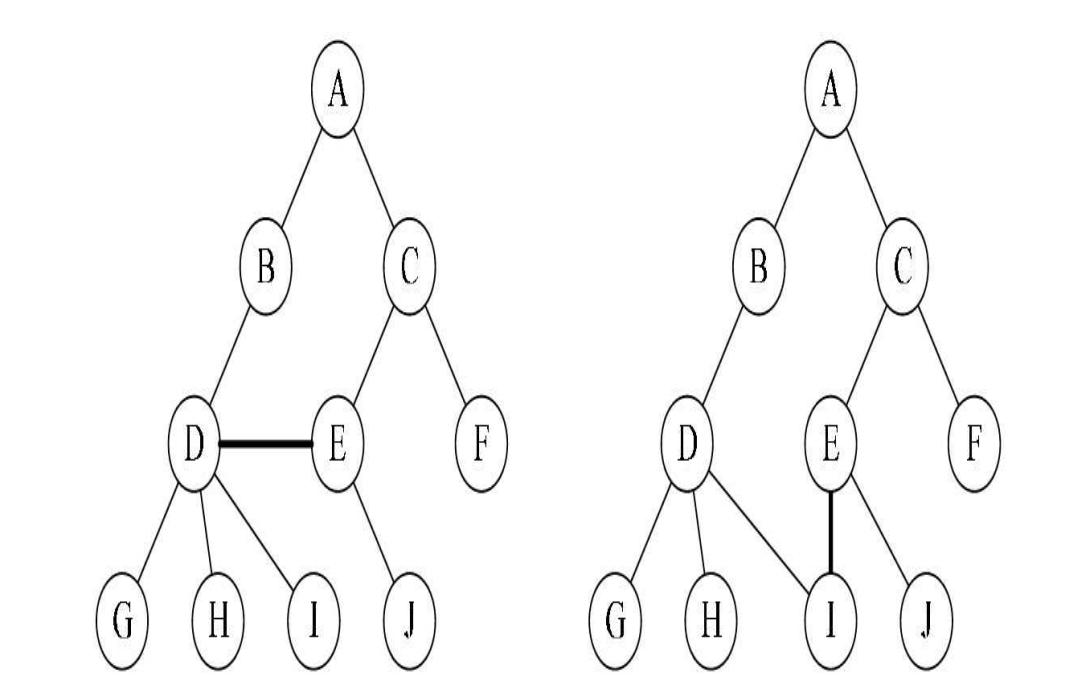
根节点一定是唯一的,不可能存在多个根节点。
子树的个数没有限制,但它们一定是互不相交的
不可能出现下面的一个树
结点的分类
在认识结点之前,我们先要认识一下度这个概念。度:结点拥有的子树数。就像之前图中的根结点的度是一个2。然后我们通过度来定义不同结点。
叶子结点 :度为0的结点。
内部结点:除根结点之外所有的结点都是内部结点。
树的度 : 树的度是树内各结点的度的最大值
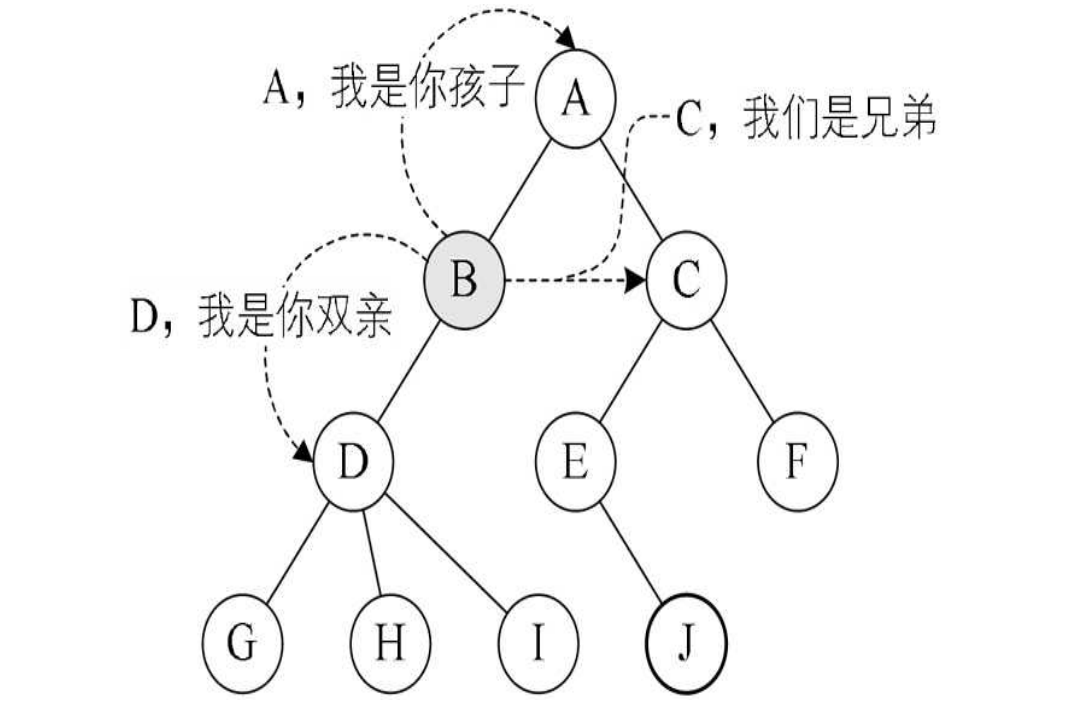
结点之间的关系
结点的子树的根称为该结点的孩子。下面这张图很好的展示了结点之间的一个关系。
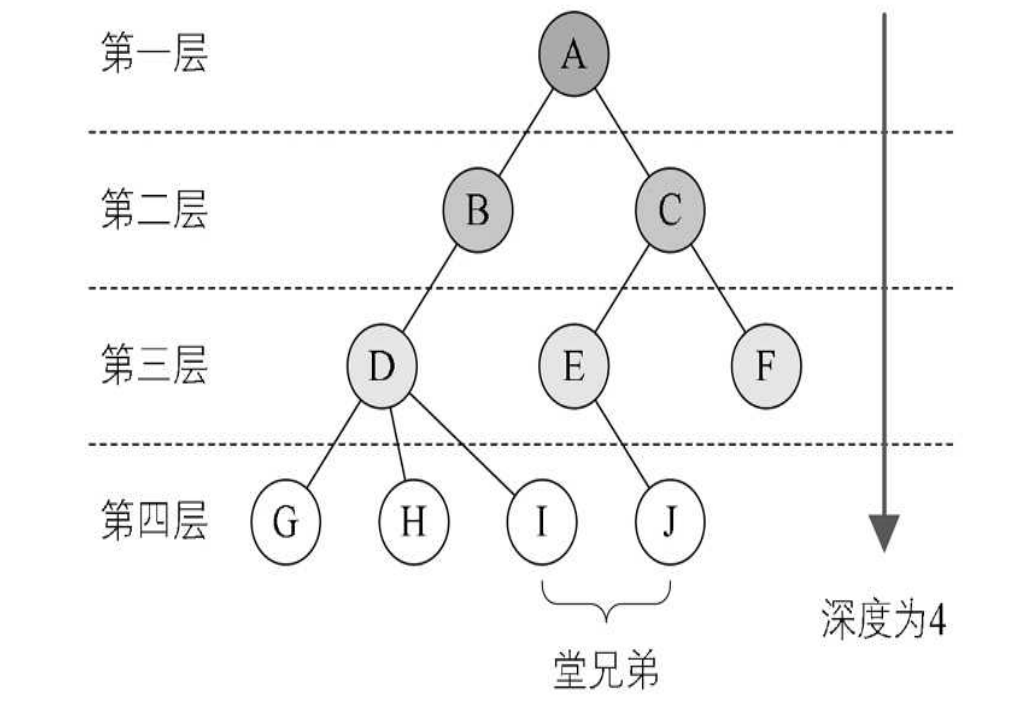
深度与高度
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。树中结点的最大层次称为树的深度(Depth)或高度,当前树的深度为4
高度 :从距离该结点最远的叶节点到该结点所经过的边的数量
二叉树
二叉树对于我们的意义
简单性:二叉树的结构相对简单,每个结点最多只有两个子结点,易于理解和实现。任何树都可与二叉树相互转换
高效性:二叉树的结构简单,许多基于二叉树的算法和数据结构具有高效性。例如,二叉搜索树的查找、插入和删除操作的时间复杂度都是O(log n),非常高效。
定义
二叉树是 n (n≥0) 个结点的有限集,它或者是空集 (n=0) ,或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。
特点
- 每个结点最多有两个孩子
- 子树有左右之分
- 子树可以为空
基本形态
空二叉树。
只有一个根结点。
根结点只有左子树。
根结点只有右子树。
根结点既有左子树又有右子树
特殊二叉树
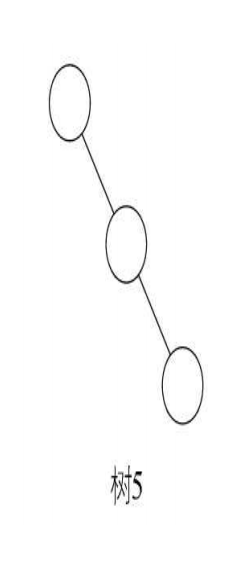
- 斜树
就是每一层都只有一个结点,结点的个数与二叉树的深度相同
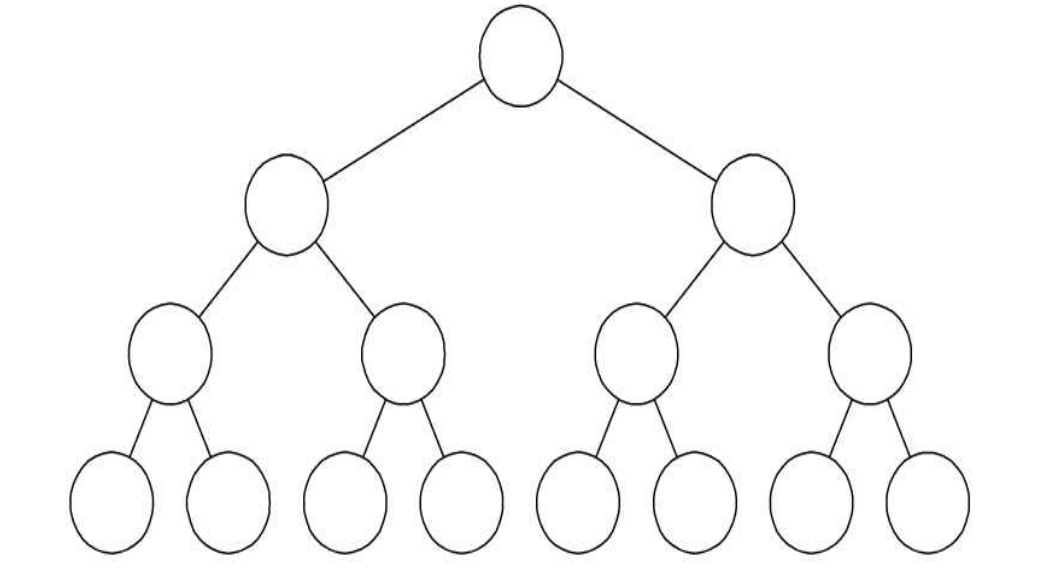
- 满二叉树
因此,满二叉树的特点有:
(1)叶子只能出现在最下一层。出现在其他层就不可能达成平衡。
(2)非叶子结点的度一定是2。否则就是“缺胳膊少腿”了
(3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多
- 完全二叉树
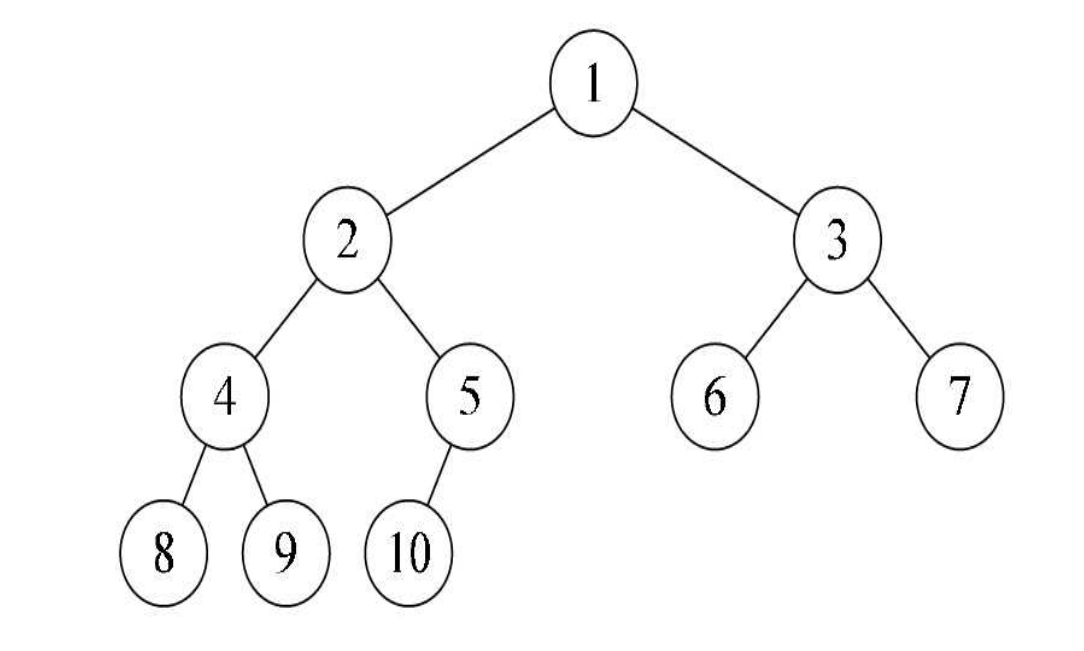
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树.
(1)叶子结点只能出现在最下两层。
(2)最下层的叶子一定集中在左部连续位置。
(3)倒数二层,若有叶子结点,一定都在右部连续位置。
(4)如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
(5)同样结点数的二叉树,完全二叉树的深度最小
二叉链表
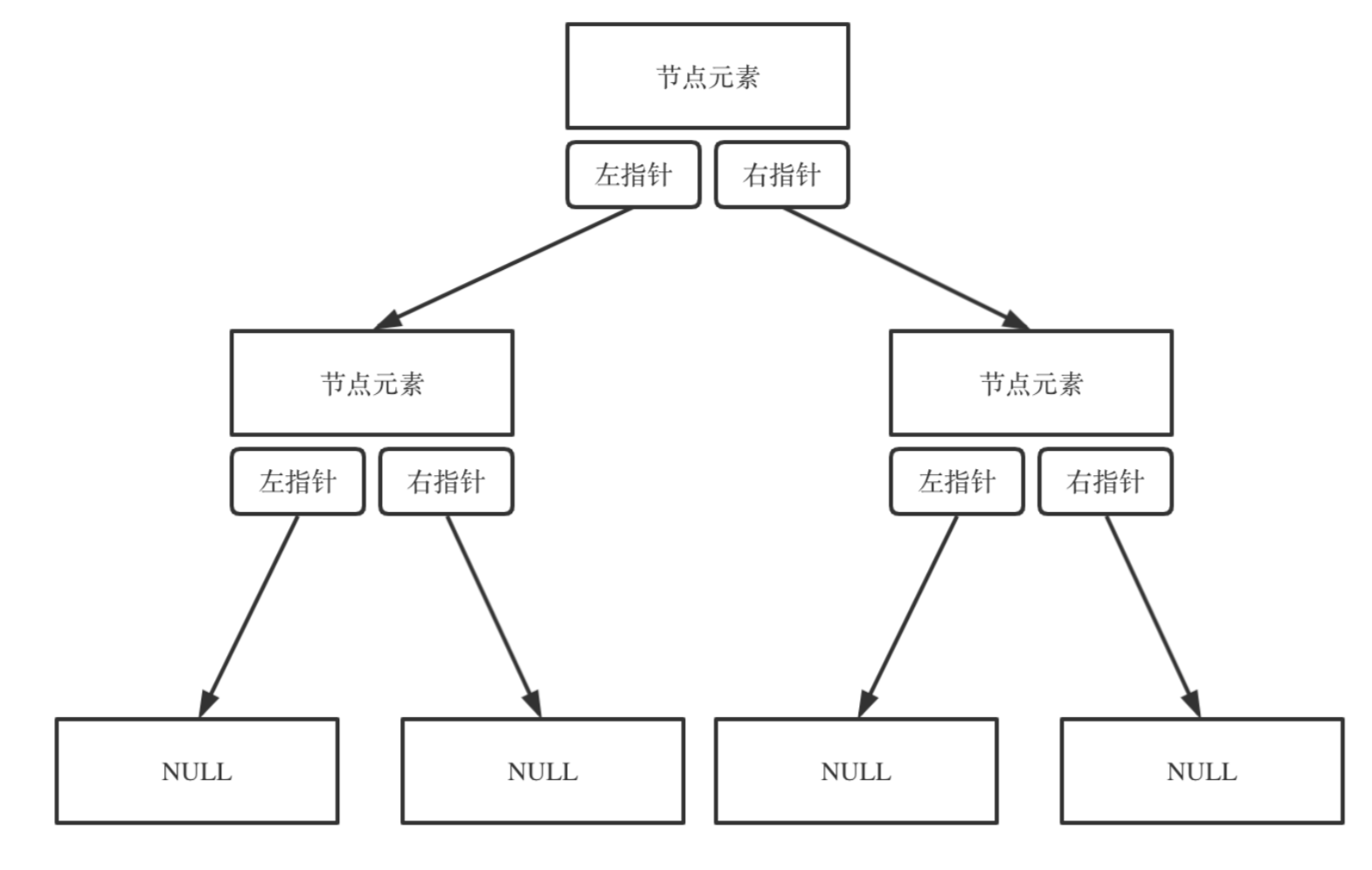
因为二叉树不适合用顺序表存储,所以我们应该采用一个二叉链表来存储我们的一个二叉树。
二叉树的链式存储结构是使用链表来表示二叉树的一种方法。在这种存储结构中,每个结点由数据域和两个指针域组成,分别用来指向该结点的左孩子结点和右孩子结点。这种结构的结点通常被称为二叉树结点。
通常我们的二叉树表示成下面这种结构
typedef struct BinaryTreeNode {
int data;
struct BinaryTreeNode *left,*right;
} BiNode;
三种遍历方式
遍历原理
- 深度优先,沿着树的深度尽可能远的搜索数的一个分支。当到达树的最深处的时候,再回溯树的上一级及结点继续搜索完成遍历,知道遍历一整棵树。
- 广度优先,从根结点开始沿着树的宽度遍历树的结点,首先访问根节点,然后依次访问与根结点相邻的结点,直到遍历完整层的节点再向下一层移动。
这两种不同的原理会让我们的二叉树的遍历结果推向不一样。
深度优先(前序,中序,后序遍历)
前序遍历
前序遍历的规则:规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。这里我们引入一道题目来帮助我们理解这个遍历二叉树的一个规则。
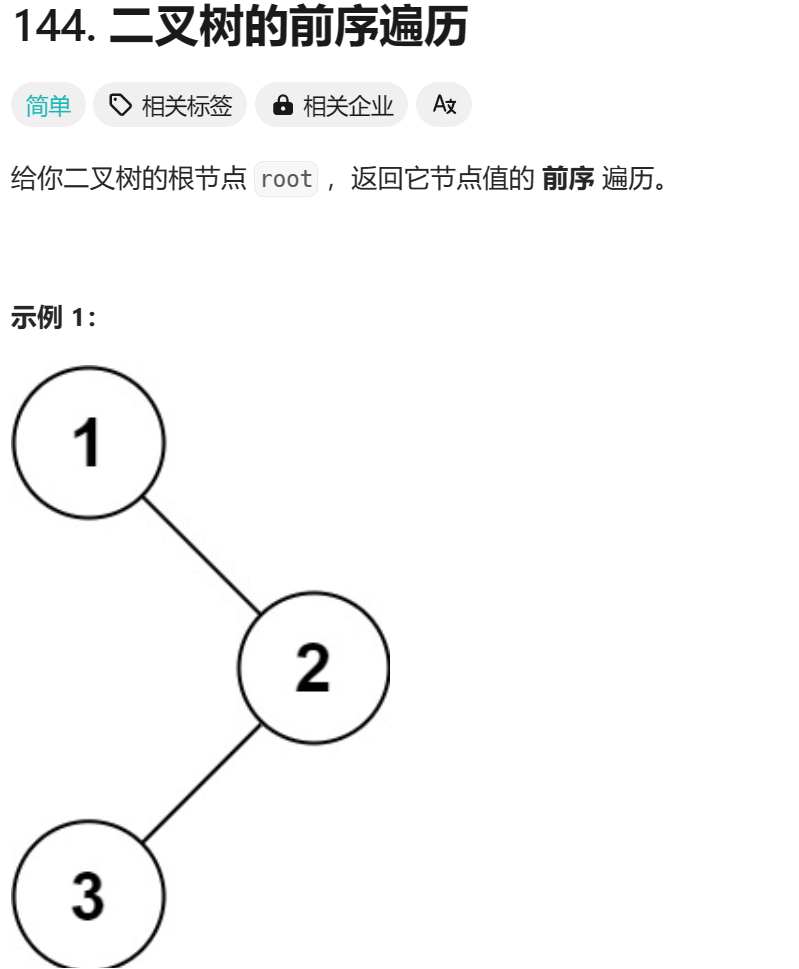
二叉树的题目我们一般采用一个递归遍历的方式来解决这类问题。
我们现在用递归三部曲来思考一下这个问题:
- 递归函数的参数和返回值
这里我们不难看出这个函数是一个空类型,每一次我们要传入的是他所在的一个结点。
void Traversal(TreeNode* root) {
;
}
- 递归的终止条件
递归的终止条件从我们上面的规则不难看出我们只要走到头就结束,所以也就是我们传入的节点是一个空就退出
if (root == NULL) {
return;
}
- 单层递归的逻辑
这里的逻辑就是我们前序遍历的一个顺序,也就是中左右的原则。我们每一次都先把中添加到我们的数组中间,然后先向左节点进行一个递的操作,在向右节点进行一个递的操作。
void Traversal (TreeNode* root, vector<int> & vec) {
if (root == NULL) {
return;
}
vec.push_back(root->val);
Traversal(root->left, vec);
Traversal(root->right, vec);
}
AC代码
class Solution {
public:
void Traversal (TreeNode* root, vector<int> & vec) {
if (root == NULL) {
return;
}
vec.push_back(root->val); //中
Traversal(root->left, vec); //左
Traversal(root->right, vec); //右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> arrary;
Traversal(root, arrary);
return arrary;
}
};
中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
其实通过递归三部曲的分析我们发现这三种遍历方式在递归写法上的唯一区别就是我们最后单层递归的一个逻辑不同。
AC代码
class Solution {
public:
void Traversal (TreeNode* root, vector<int> & vec) {
if (root == NULL) {
return;
}
Traversal(root->left, vec); //左
vec.push_back(root->val); //中
Traversal(root->right, vec); //右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> arrary;
Traversal(root, arrary);
return arrary;
}
};
后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。
AC代码
class Solution {
public:
void Traversal (TreeNode* root, vector<int> & vec) {
if (root == NULL) {
return;
}
Traversal(root->left, vec); //左
Traversal(root->right, vec); //右
vec.push_back(root->val); //中
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> arrary;
Traversal(root, arrary);
return arrary;
}
};
注:二叉树可以采用一个迭代遍历的方式 ,我们采用一个栈的先进后出的结构来实现这个二叉树的一个遍历(因为递归的特性和栈一样是一个先进后出)下面给出代码。
我们现在对这个部分进行一个分析,入栈出栈的一系列的一些条件。
前序遍历很简单,我们发现我们按照我们的顺序进行一个遍历,也就是中左右的顺序进行遍历即可。
前序遍历
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> stk;
vector<int> vec;
if (root == NULL) {
return vec;
}
stk.push(root); //入栈一个根节点
while (!stk.empty()) { //栈不为空
TreeNode* tmp = stk.top(); //出栈根结点,然后分别将他的左右子树的根节点入栈
stk.pop();
vec.push_back(tmp->val);
if (tmp->right) {
stk.push(tmp->right);
}
if (tmp->left) {
stk.push(tmp->left);
}
}
return vec;
}
};
中序遍历
而中序遍历就比较复杂了,我们发现我们不能像递归一样稍微修改一下就可以得出一个答案了,因为我们发现采用上面那种方法会出问题。所以这一次中序遍历我们则需要一个指针来进行一个迭代操作,这个指针用来记录我们的位置然后用栈进行一个数据的记录
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) { // 指针来访问节点,访问到最底层
st.push(cur); // 将访问的节点放进栈
cur = cur->left; // 左
} else {
cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)
st.pop();
result.push_back(cur->val); // 中
cur = cur->right; // 右
}
}
return result;
}
};
后序遍历
后序遍历的迭代可以采用和前序遍历一样的思路,同样是一次遍历便可以实现一个结果,最后我们进行一个反转数组的操作便可以实现了。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) {
st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
}
if (node->right) {
st.push(node->right); // 空节点不入栈
}
}
reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
return result;
}
};
广度优先(层序遍历)
广度优先我们采用一个队列的数据结构实现遍历,记录每一层的节点然后依次入队出队。
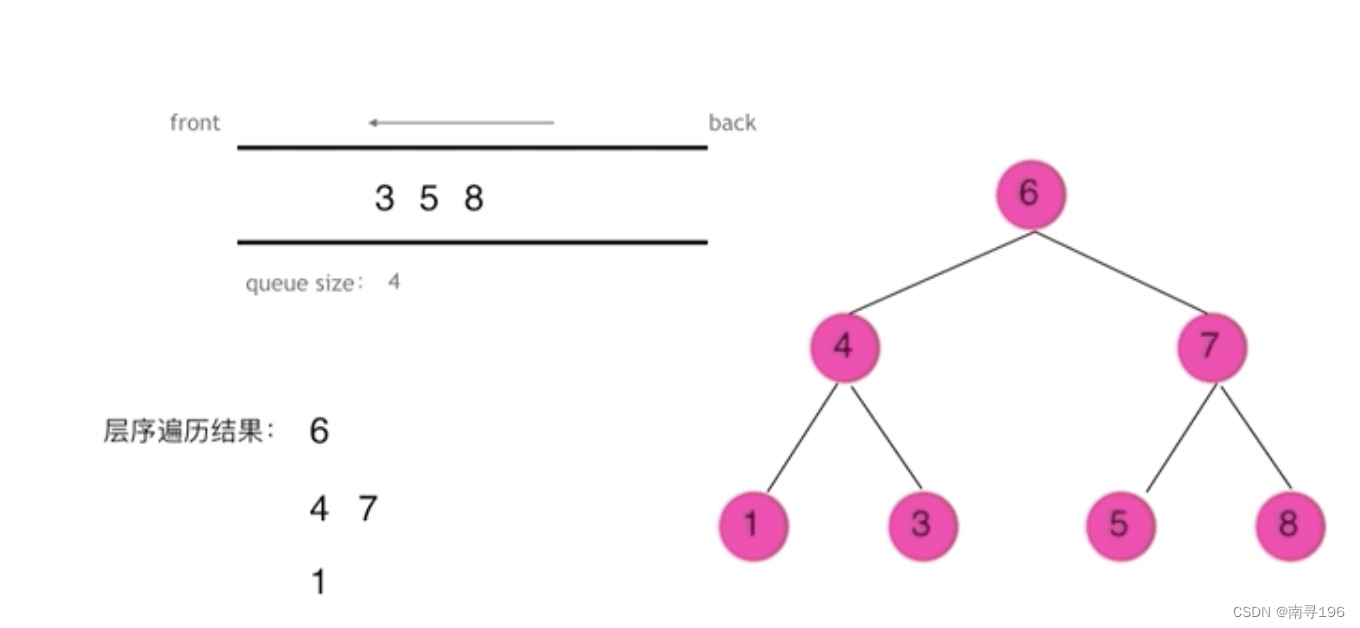
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) {
que.push(root);
}
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size(); // 记录长度
vector<int> vec;
for (int i = 0; i < size; i++) { //这里的size一定要使用上面记录的,不能用que.size()因为这个会时刻变化
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) {
que.push(node->left);
}
if (node->right) {
que.push(node->right);
}
}
result.push_back(vec);
}
return result;
}
};
小结
这里主要是认识二叉树以及遍历二叉树的三种方法进行了一个讲解,仅仅只是二叉树的一个入门知识,后面还有B+树和线索二叉树以及平衡二叉树需要我去学习,后续会继续进行补充。