已知

1. 有四个虫子,分别是$A,B,C,D$
2. $A,B,C,D$分别在$(0,0),(0,1),(1,1),(1,0)$
3. 四个虫子A追B，B追C，C追D，D追A
4. 四个速度相同

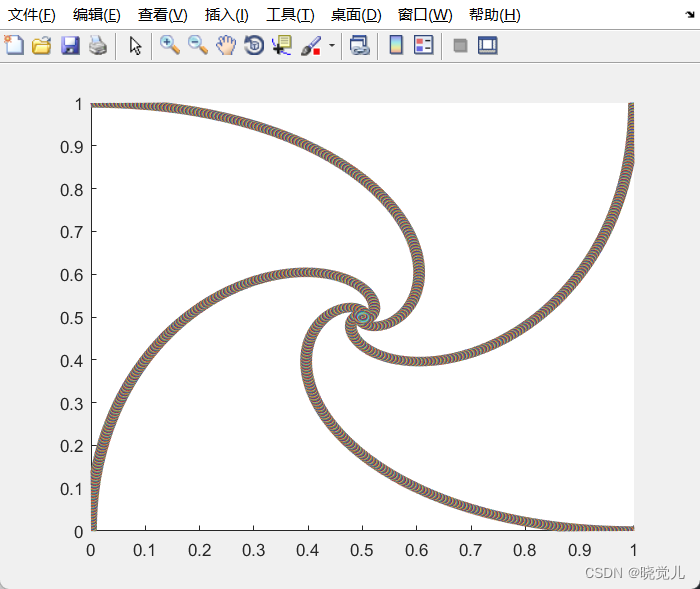
问题1:虫子追逐轨迹图

建立追击模型:
设在$t$时刻时候，虫子$A(x_a,y_a)$追虫子$B(x_b,y_b)$，求下一时刻$t+\Delta t$时候虫子$A$的坐标$(x,y)$
连接$A,B$两点，可以求出运动方向(角度),利用运动方向求下一刻坐标

$\{\begin{array}{l}\cos \alpha =(x_b-x_a)/\sqrt{(x_b-x_a{)}^2+(y_b-y_a{)}^2}\\ \sin \alpha =(y_b-y_a)/\sqrt{(x_b-x_a{)}^2+(y_b-y_a{)}^2}\end{array}$

$\{\begin{array}{l}\cos \alpha =(x-x_a)/\sqrt{(x-x_a{)}^2+(y-y_a{)}^2}\\ \sin \alpha =(y-y_a)/\sqrt{(x-x_a{)}^2+(y-y_a{)}^2}\end{array}$
按照物理模型
$\{\begin{array}{l}x=x_a+cos(\alpha )\ast \Delta t\ast v\\ y=y_a+sin(\alpha )\ast \Delta t\ast v\end{array}$

速度相同，消除速度得到最终模型
$\{\begin{array}{l}x=x_a+(x_b-x_a)/\sqrt{(x_b-x_a{)}^2+(y_b-y_a{)}^2}\ast \Delta t\\ y=y_a+(y_b-y_a)/\sqrt{(x_b-x_a{)}^2+(y_b-y_a{)}^2}\ast \Delta t\end{array}$

MATLAB:

x = [0,0,1,1];
y = [0,1,1,0];
detat = 0.001;%Δt
round = 0:pi/180:2*pi;
xlim([0,1]);
ylim([0,1]); 
hold on;
for i= 1:4
    plot(x(i),y(i));
end
flag = false;
for t=1:0.1:200
    for i= 1:4
        j = mod(i,4)+1;
        x(i) = x(i) + (x(j)-x(i))/sqrt((x(j)-x(i))^2+(y(j)-y(i))^2)*detat;
        y(i) = y(i) + (y(j)-y(i))/sqrt((x(j)-x(i))^2+(y(j)-y(i))^2)*detat;
        plot(x(i)+ 0.01*cos(round),y(i)+ 0.01*sin(round));
        if sqrt((x(j)-x(i))^2+(y(j)-y(i))^2)<=0.001%判断碰撞
            flag = true;
            break;
        end
    end
    if flag
        break;
    end
end