0.基础概念(复习一下)
1.小批量随机梯度下降

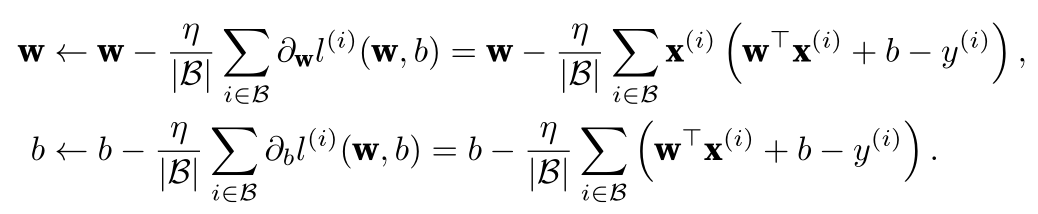
目的: 希望找到最佳的参数,使损失函数最小。
使损失函数对w求导(b就是x等于1的w),一个小批次的/eta(学习率)*小批次的平均梯度(/beta是小批次的样本数量)
遍历完全部批次的为一个epoch
2.反向传播的实现

一个一个运算子,pytorch是隐式构造
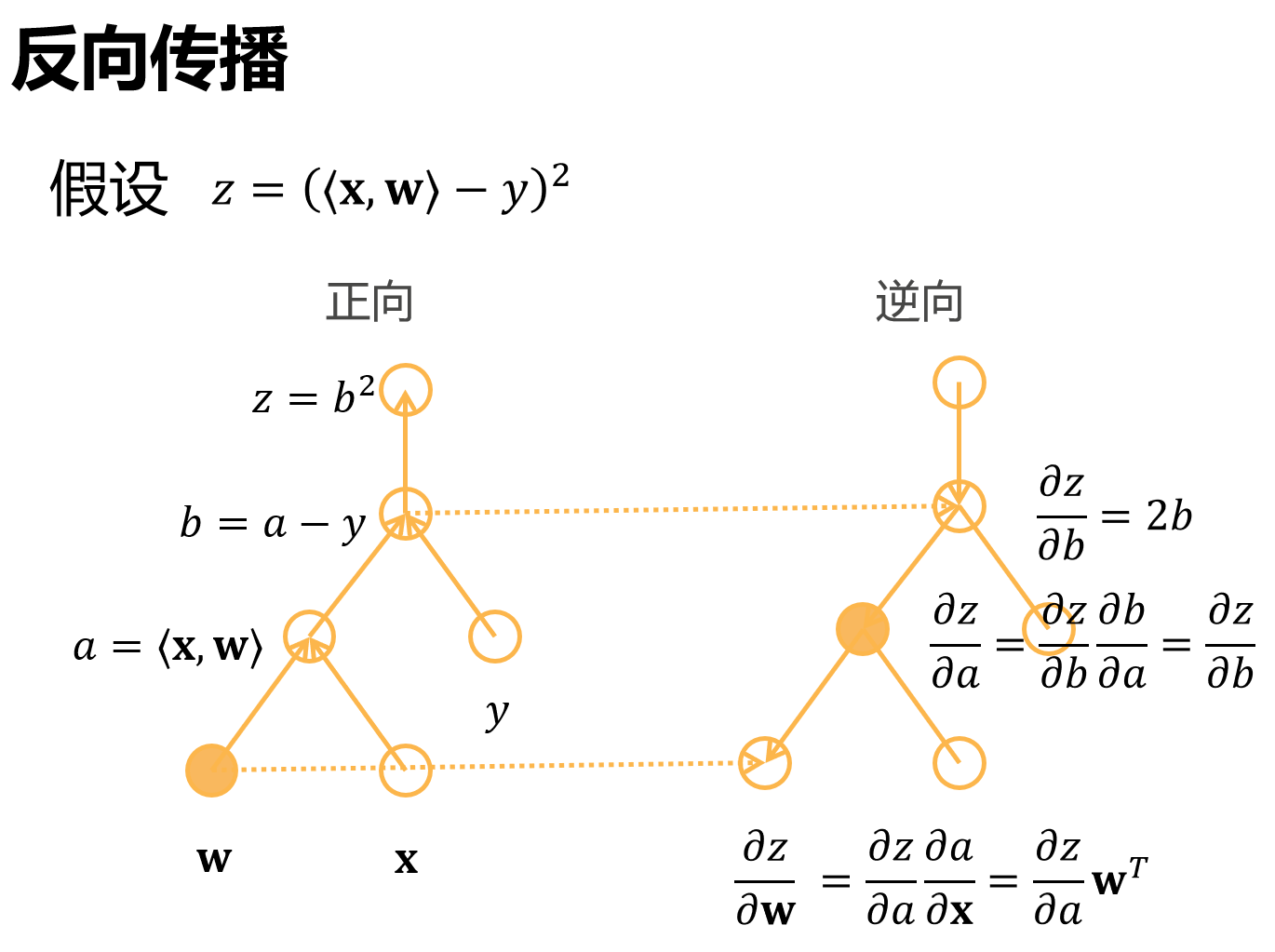
正向传播
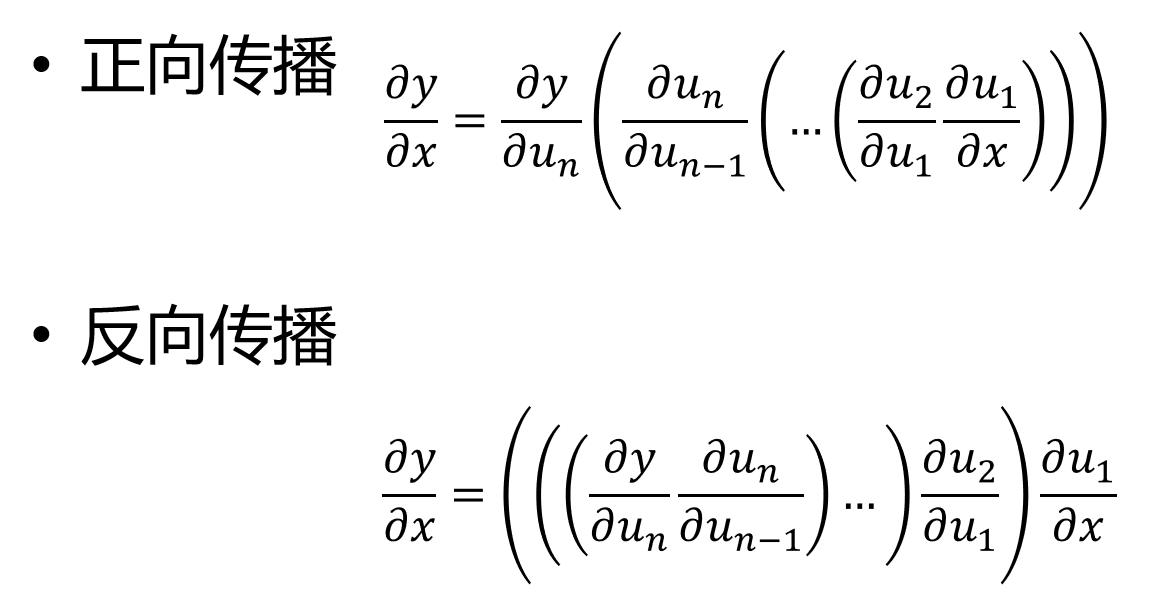
正向传播一般不存在,应为他更新一个参数就要从头算一次,更新大量参数计算量太大
反向传播复杂度:
时间复杂度 : O(n) , 计算所有导数 , 基本上与正向复杂度一致内存复杂度 : O(n) , 需要储存所有正向计算的中间值对比正向传播 :时间复杂度 : O(n) , 计算 k 个变量的导数为 O(n*k)内存复杂度 : O(1)
放弃一部分中间值• 内存是逆向传播的瓶颈• 随着层数和批量大小线性增长• 有限 GPU 内存 ( 最多 32GB )• 用算力换内存• 只保存一部分中间计算值• 当需要时重新计算未保存中间值
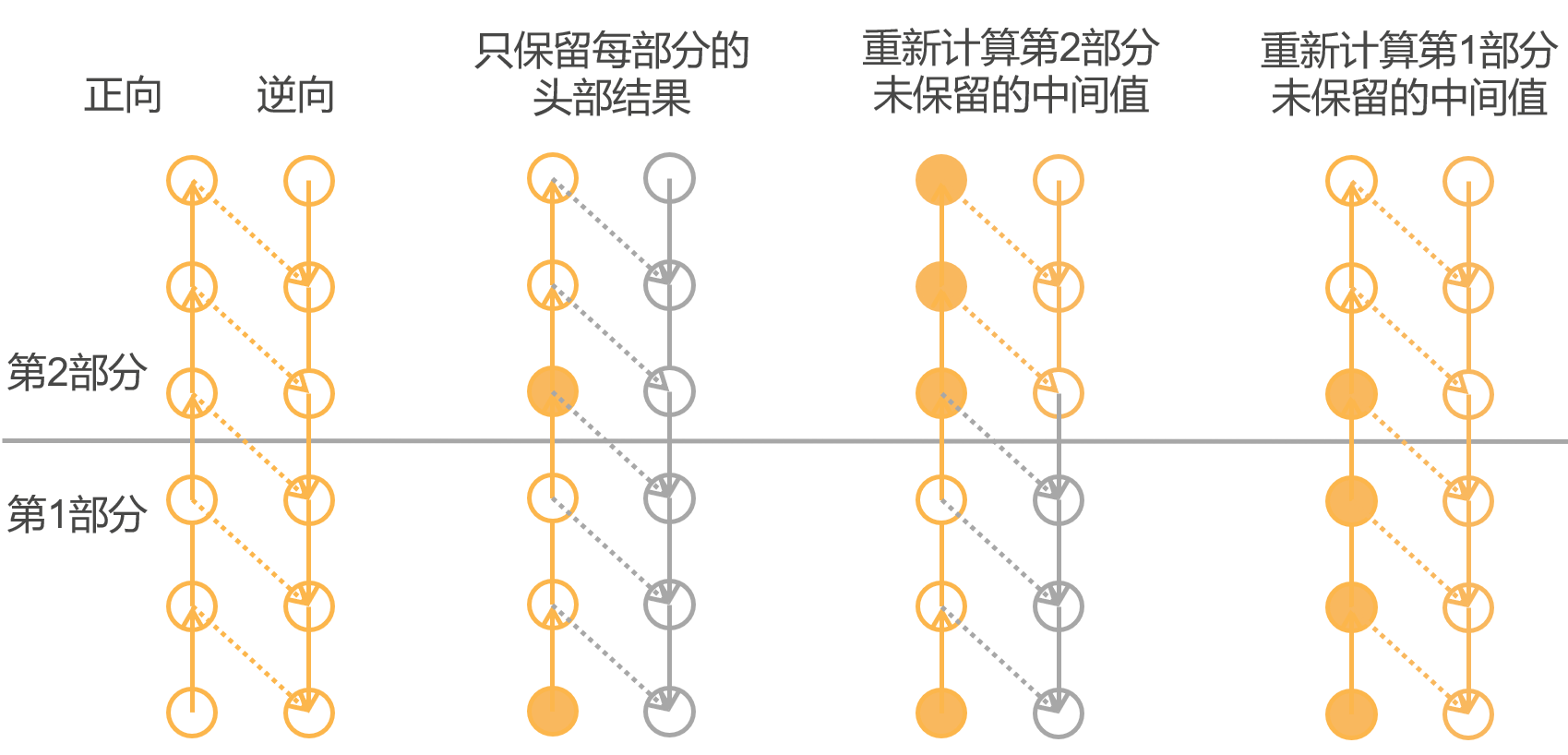
从头部开始第二次正向,反向传播,算是一个小的梯度下降
在PyTorch中有个简单的规定,不让张量对张量求导,只允许标量对张量求导。
import torch
x = torch.arange(4.0)
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad # 默认值是None
y = 2 * torch.dot(x, x)
y
tensor(28., grad_fn=<MulBackward0>)
y.backward()
x.grad
tensor([ 0., 4., 8., 12.])
x.grad == 4 * x
tensor([True, True, True, True])
x.grad.zero_()# _ 的方法通常表示原地操作,一种约定俗成的写法
y = x.sum()
y.backward()
x.grad
tensor([1., 1., 1., 1.])对x向量开启梯度下降,对y反向传播(y对X求导),把梯度存入x.grad中,shape和x一样。之后清空x.grad 再次记录梯度。
目标量对一个非标量调用backward(),则需要传入一个gradient参数。传入这个参数就是为了把张量对张量的求导转换为标量对张量的求导。
# 对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和,所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad
tensor([0., 2., 4., 6.])y现在是一个一维张量了,把所有y对x的导数加在一起就好
把y理解为多个损失函数就好 ,最后加在一起
分离计算
y是作为x的函数计算的,而z则是作为y和x的函数计算的。我们想计算z关于x的梯度,但由于某种原因,希望将y视为一个常数,并且只考虑到x在y被计算后发挥的作用。
这里可以分离y来返回一个新变量u,该变量与y具有相同的值,但丢弃计算图中如何计算y的任何信息。换句话说,梯度不会向后流经u到x。因此,下面的反向传播函数计算z=u*x关于x的偏导数,同时将u作为常数处理,
而不是z=x*x*x关于x的偏导数。(正向传播x>y,x>z,即z对x有两条传播途径,分别是y,2x*x,相加就是结果,现在把对y求导那条路断了,结果只有y了,也就是x^2,也就是u)
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u
#tensor([True, True, True, True])
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
#tensor([True, True, True, True])自动微分的一个好处
即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。即使一堆循环,也可以得到变量梯度k(d=ka)
也就是可以把这一堆循环变成一个计算f(a),得到a的梯度
a = torch.randn(size=(), requires_grad=True)
# 使用torch.randn()
函数生成一个随机的标量张量。size=()参数指定了张量的形状为空,表示创建一个标量(0维张量)
d = f(a)
d.backward()我们现在可以分析上面定义的f函数。 请注意,它在其输入a中是分段线性的。 换言之,对于任何a,存在某个常量标量k,使得f(a)=k*a,其中k的值取决于输入a,因此可以用d/a验证梯度是否正确。
a.grad == d / a输出结果:
tensor(True)
3.DataLoader
data.DataLoader得到一个数据迭代器对象,小批次取出数据
import torchvision
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
#train=True 时,表示加载训练数据集;而当 train=False 时,表示加载测试数据集。
# 准备的测试数据集 数据放在了CIFAR10文件夹下
test_data = torchvision.datasets.CIFAR10("./CIFAR10",
train=False, transform=torchvision.transforms.ToTensor())
test_loader = DataLoader(dataset=test_data, batch_size=4,
shuffle=True, num_workers=0, drop_last=False)
#创建一个迭代器对象,test_loader,遍历数据,每次4张
# 测试数据集中第一张图片及target
img, target = test_data[0]
print(img.shape)
print(target)
# 在定义test_loader时,设置了batch_size=4,表示一次性从数据集中取出4个数据
for data in test_loader:
imgs, targets = data
print(imgs.shape)
print(targets)
# 在定义test_loader时,设置了batch_size=4,表示一次性从数据集中取出4个数据
writer = SummaryWriter("logs")
for epoch in range(2):
step = 0
for data in test_loader:
imgs, targets = data
writer.add_images("Epoch: {}".format(epoch), imgs, step)
step = step + 1
writer.close() 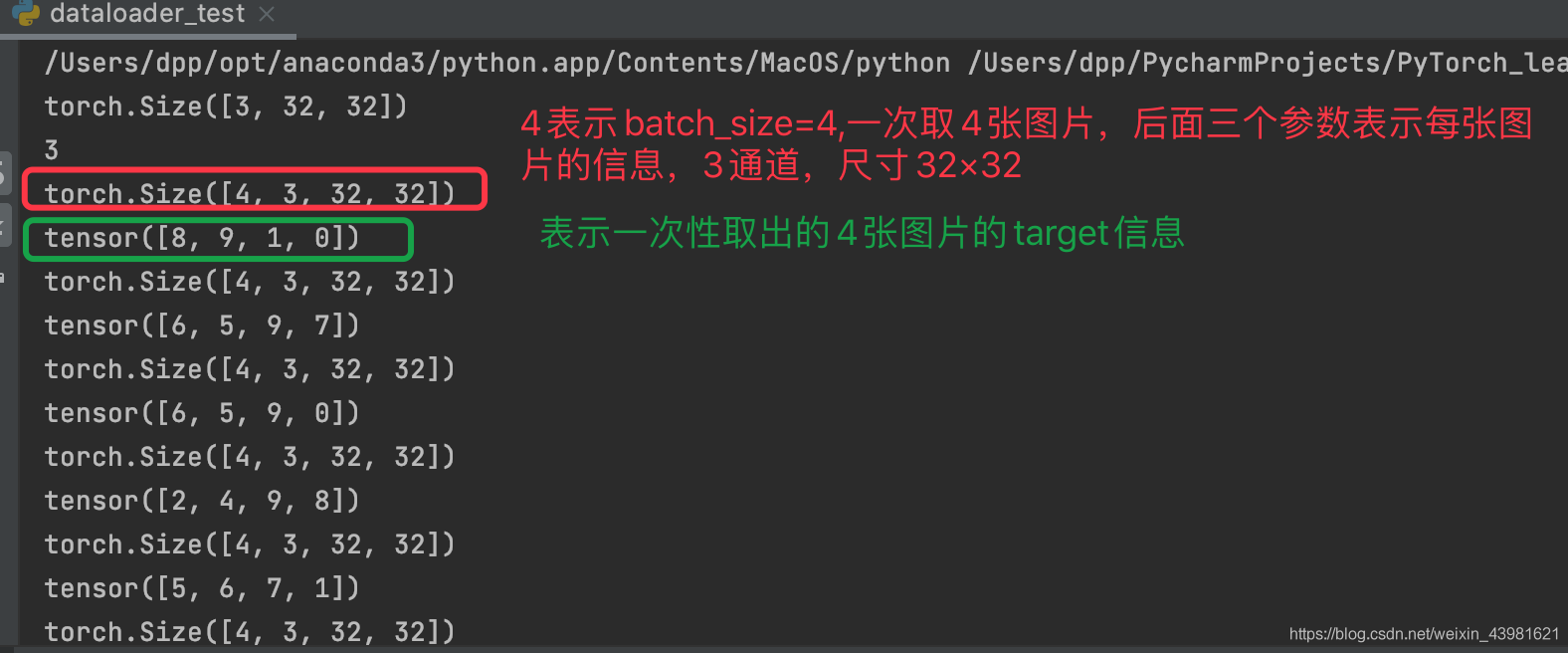
4.线性模型和非线性模型
softmax回归中,虽然加入了softmax,但是大小的顺序并没有改变,仍是线性模型,然而我们可以很容易找出违反单调性的例子。
例如,对猫和狗的图像进行分类:增加位置(13,17)处像素的强度是否总是增加(或降低)图像描绘狗的似然?对线性模型的依赖对应于一个隐含的假设,即区分猫和狗的唯一要求是评估单个素的强度。在一个倒置图像后依然保留类别的世界里,这种方法注定会失败。所以,这里的线性很荒谬
因此,我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系类型。
5.激活函数

如果没有激活函数,在添加隐藏层之后,我们没有好处!
因为仿射函数的仿射函数本身就是仿射函数,但是我们之前的线性模型已经能够表示
任何仿射函数。
![]()
为了发挥多层架构的潜力,我们需要非线性的激活函数
即使是网络只有一个隐藏层,给定足够的神经元和正确的权重,我们可以对任意函数建模,尽管实际中学习该函数是很困难的。而且,虽然一个单隐层网络能学习任何函数,但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。事实上,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。
6.欠拟合和过拟合
模型不能降低训练误差,这可能意味着模型过于简单(即表达能力不足),无法捕获试图学习的模式。此外,由于我们的训练和验证误差之间的泛化误差很小,我们有理由相信可以用一个更复杂的模型降低训练误差。这种现象被称为欠拟合(underfitting)。
另一方面,当我们的训练误差明显低于验证误差时要小心,这表明严重的过拟合(overfitting)。注意,过拟合并不总是一件坏事。特别是在深度学习领域,众所周知,最好的预测模型在训练数据上的表现往往比在保留(验证)数据上好得多。最终,我们通常更关心验证误差,而不是训练误差和验证误差之间的差距。
7.权重衰减(weight decay)(L 2 正则化)
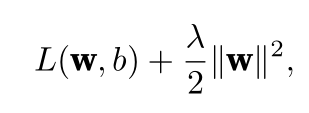
lambd = 0禁用权重衰减后运行这个代码。注意,这里训练误差有了减少,但测试误差没有减少,
这意味着出现了严重的过拟合。减少过拟合
8.暂退法(Dropout)
经典泛化理论认为,为了缩小训练和测试性能之间的差距,应该以简单的模型为目标。简单性以较小维度的形式展现。此外,正如权重衰减(L 2 正则化)时,参数的范数也代表了一种有用的简单性度量。
简单性的另一个角度是平滑性,即函数不应该对其输入的微小变化敏感。即当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的。
在训练过程中,在计算后续层之前向网络的每一层注入噪声。因为当训练一个有多层的深层网络时,注入噪声只会在输入‐输出映射上增强平滑性。这个想法被称为暂退法(dropout)。
在标准暂退法正则化中,每个中间活性值h以暂退概率p由随机变量h ′ 替换

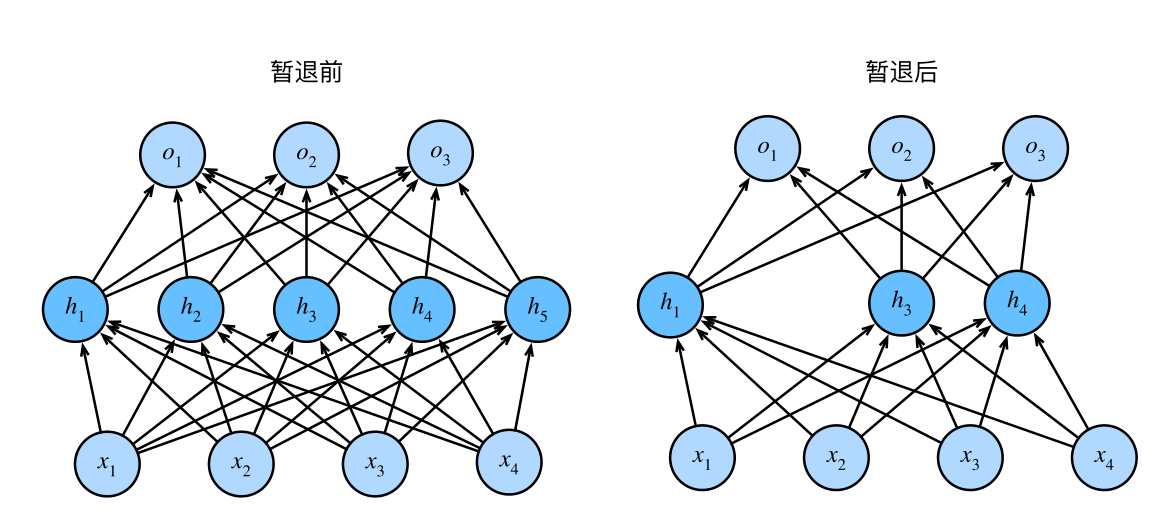
测试时(预测时)不用暂退法。给定一个训练好的模型和一个新的样本,我们不会丢弃任何节点,因此不需要标准化。
9.卷积输入通道和输出通道
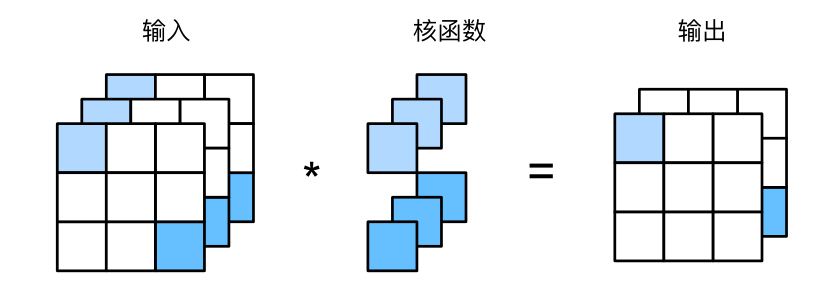
1.构建alexnet网络
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
# 这里使用一个11*11的更大窗口来捕捉对象。
# 同时,步幅为4,以减少输出的高度和宽度。
# 另外,输出通道的数目远大于LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口。
# 除了最后的卷积层,输出通道的数量进一步增加。
# 在前两个卷积层之后,汇聚层不用于减少输入的高度和宽度
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# 这里,全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# 最后是输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10))
X = torch.randn(1, 1, 224, 224)
for layer in net:
X=layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape)
Conv2d output shape: torch.Size([1, 96, 54, 54])
ReLU output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Conv2d output shape: torch.Size([1, 256, 26, 26])
ReLU output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 256, 12, 12])
ReLU output shape: torch.Size([1, 256, 12, 12])
MaxPool2d output shape: torch.Size([1, 256, 5, 5])
Flatten output shape: torch.Size([1, 6400])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])2.读取数据集
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)3.训练数据集
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward() #把梯度下降值存到grad里
optimizer.step()#-grad更新参数
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())



![[2024更新]如何从Android恢复已删除的相机照片?](https://img-blog.csdnimg.cn/direct/3c0f9cd2ecb747a48c1886bd0e1e31a7.png)