【LeetCode 684. 冗余连接】

思路：

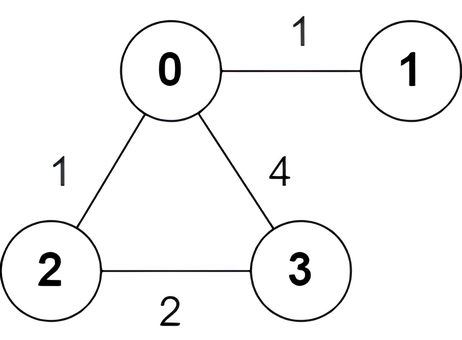
首先因为这是一个无向图，所以不需要考虑谁是树根。

那么我们一条条边加入到图里去，直到出现了环为止，那么这条边就是冲突的边，需要删除掉。

那么怎么判断是否出现了环呢？如果加入一条边 [u , v] 的时候，两个结点所在的连通块不是同一个，那么一定没有环。否则的话，两个结点连在了同一棵子树上，那么一定会产生一个环。

如何高效的判断两个结点是否在同一棵子树上呢？这就需要用到一个数据结构——并查集。

并查集采用一个数组 f[i] 来表示结点 i 的父结点。那么初始的时候没有任何边，定义所有结点的父结点等于它自身：f[i] = i 。

当加入一条边 [u , v] 的时候，可以沿着 u -> f[u] ->f[f[u]] -> … 的路径递归找到 u 所在子树的根结点 ru（ v 同理得到 rv ），然后只需要判断两个根结点是否相同就行了。如果根结点相同，那么就产生环了，直接输出这个冲突边就行。否则的话就要把这两棵子树连到一起，最简单的做法就是直接把 ru 连到 rv 下面，当作它的子结点，那么就需要更新 f[ru] = rv 。

下面讲两个常用的并查集优化。

路径压缩： 因为我们无需关注每一棵子树结构是什么样的，我们只关注它的根结点是谁。所以为了减小查找根结点的时间，每个结点离根结点要尽量近。

那么我们定义查找根结点函数 find(u) ，如果 u = f[u] ，那么不用找了，它自己就是根结点。否则的话调用 find(f[u]) 递归寻找子树的根结点。最后做一步路径压缩的优化，把根结点当作 u 的父结点： f[u] = find(f[u]) 。这样下次再查找的时候，路径长度就变为了 1 ，一步就能找到根结点了。

按秩合并： 合并两棵子树的时候，为了使得合并后的子树高度尽量小，需要把高度小的那棵子树接在高度高的那棵下面，当作儿子。

所以定义一个 rank[i] 数组，用来记录 i 这个结点作为根结点的子树高度，初始时全都是 1 。那么在合并的时候，把 rank 值小的接到大的下面去，如果一样怎么办呢？随便接，然后把合并后的根结点 rank 值加 1 就行了。

代码实现：

申请两个全局数组记录父节点和树高；

static const int N = 1010;
int f[N], rank[N];

主函数；

vector<int> findRedundantConnection(vector<vector<int>>& edges) {
    init();
    for (auto e : edges) {
        int u = e[0], v = e[1];
        if (same(u, v)) return {u, v};
        else join(u, v);
    }
    return {-1, -1};
}

初始化每个节点为一棵新的树；

    void init() {
        for (int i = 0; i < N; ++i) {
            f[i] = i;
            rank[i] = 1;
        }
    }

寻找父节点的功能函数；

    int find(int u) {
        return u==f[u] ? u : f[u]=find(f[u]);
    }

合并树；

void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return;
    if (rank[u] < rank[v]) {
        f[u] = v;
    } else {
        f[v] = u;
        if (rank[u] == rank[v]) {
            rank[u]++;
        }
    }
}

判断输入的节点对中的两个节点是否属于同一个根节点；

bool same(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

提交总览：

至此，本题结束。

【LeetCode 685. 冗余连接 II】

思路：

这题是上一道题 684. 冗余连接 - 力扣（LeetCode）的进阶版，区别就是无向图变成了有向图。

上一道题解说过，无向图能构成一棵树的条件是没有环，那么有向图的条件是什么呢？

首先还是得没有环，其次因为是边是有向的，所以一个结点只能有一个父结点（也就是入度为 1 ）。那么这题解法就有了。

• 首先判断有没有入度为 2 的结点，如果有的话，那两条边一定有一条得删掉。
• 按照出现时间从后到前看那两条边，删掉其中一条之后是否能构成一棵树（也就是无环）。如果删掉了无环，那就直接返回这条边作为答案。
• 如果入度全是 1 ，那就直接按照出现时间从前到后看添加了哪一条边之后开始出现了环，那么那条边就是答案。

判断能否构成一棵树的话还是用并查集，唯一区别就是不需要用按秩合并的优化了，而且给定有向边 [u , v]，只能把 v 接在 u 下面。

代码实现：

申请记录父节点和入度；

    static const int N = 1010;
    int f[N], degree[N];
    int n;

主函数；

vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
    n = edges.size();
    memset(degree, 0, sizeof degree);
    for (auto e : edges) ++degree[e[1]];
    for (int i = n-1; i >= 0; --i) {
        if (degree[edges[i][1]] == 2 && !wrongEdge(edges, i).size()) {
            return edges[i];
        }
    }
    return wrongEdge(edges, n);
}

判断是否无环的功能函数；

    vector<int> wrongEdge(vector<vector<int>>& edges, int except) {
        init();
        for (int i = 0; i < n; ++i) {
            if (i == except) continue;
            int u = edges[i][0], v = edges[i][1];
            if (same(u, v)) return edges[i];
            join(u, v);
        }
        return {};
    }

同上题功能相似的四个基础的功能函数，注意这里是有向图，所以 join 函数写法不同；

void init() {
    for (int i = 1; i <= n; ++i) {
        f[i] = i;
    }
}

int find(int u) {
    return u==f[u] ? u : f[u]=find(f[u]);
}

void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return;
    f[v] = u;
}

bool same(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

提交总览：

至此，本题结束。

并查集算法系列到此结束！！