Leetcode 第 394 场周赛
- 1. [统计特殊字母的数量 I](https://leetcode.cn/problems/count-the-number-of-special-characters-i/)
- 2. [统计特殊字母的数量 II](https://leetcode.cn/problems/count-the-number-of-special-characters-ii/)
- 3. [使矩阵满足条件的最少操作次数](https://leetcode.cn/problems/minimum-number-of-operations-to-satisfy-conditions/)
- 4. [最短路径中的边](https://leetcode.cn/problems/find-edges-in-shortest-paths/)
本次周赛是手速场,奈何我卡在第三题实在是太久了,其实第四题比第三题要简单,第四题图论题就是非常简单的单次迪杰斯特拉+父节点回溯,第三题是动态规划反而不太好想出来,一开始写了半天的 DFS 遍历结果只能过 50% 的用例……
- 统计特殊字母的数量 I
- 统计特殊字母的数量 II
- 使矩阵满足条件的最少操作次数
- 最短路径中的边
1. 统计特殊字母的数量 I
给你一个字符串 word。如果 word 中同时存在某个字母的小写形式和大写形式,则称这个字母为 特殊字母 。
返回 word 中 特殊字母 的数量。
示例 1:
输入: word = “aaAbcBC”
输出: 3
解释:
word 中的特殊字母是 'a'、'b' 和 'c'。
示例 2:
输入: word = “abc”
输出: 0
解释:
word 中不存在大小写形式同时出现的字母。
示例 3:
输入: word = “abBCab”
输出: 1
解释:
word 中唯一的特殊字母是 'b'。
提示:
1 <= word.length <= 50word仅由小写和大写英文字母组成。
模拟题,没啥好说的,看完题之后再仔细读几遍题,确保没有坑之后就可以开始动手实现了,比较简单。
class Solution {
public:
int numberOfSpecialChars(string word) {
vector<int> lowerMark(26);
vector<int> upperMark(26);
for (const char& c : word) {
if ((int)c >= 97)
lowerMark[(int)c - 97] = 1;
else
upperMark[(int)c - 65] = 1;
}
int ans = 0;
for (int i = 0; i < 26; ++i)
ans += lowerMark[i] & upperMark[i];
return ans;
}
};
2. 统计特殊字母的数量 II
给你一个字符串 word。如果 word 中同时出现某个字母 c 的小写形式和大写形式,并且 每个 小写形式的 c 都出现在第一个大写形式的 c 之前,则称字母 c 是一个 特殊字母 。
返回 word 中 特殊字母 的数量。
示例 1:
输入: word = “aaAbcBC”
输出: 3
解释:
特殊字母是 'a'、'b' 和 'c'。
示例 2:
输入: word = “abc”
输出: 0
解释:
word 中不存在特殊字母。
示例 3:
输入: word = “AbBCab”
输出: 0
解释:
word 中不存在特殊字母。
提示:
1 <= word.length <= 2 * 105word仅由小写和大写英文字母组成。
非常好模拟题,使我的数组旋转。还是简单的模拟题,开两个数组,分别记录小写字母最后一次出现的位置以及大写字母第一次出现的位置,最后统计两个数组对应位置上符合题目的 “小写字母最后一次位置小于大写字母第一次位置” 的数量即可(由于我初始化为 -1 ,因此还需额外判断是否存在,而不只是简单的小于关系,否则 − 1 < 0 -1<0 −1<0 这种也被判定为合法就是错的,因为 − 1 -1 −1 代表这个字符没有出现在字符串中)。
class Solution {
public:
int numberOfSpecialChars(string word) {
vector<int> lowerMark(26, -1);
vector<int> upperMark(26, -1);
int len = word.length();
for (int i = 0; i < len; ++i) {
if ((int)word[i] >= 97)
lowerMark[(int)word[i] - 97] = i;
else if (upperMark[(int)word[i] - 65] < 0)
upperMark[(int)word[i] - 65] = i;
}
int ans = 0;
for (int i = 0; i < 26; ++i)
ans += (int)(lowerMark[i] >= 0 && upperMark[i] >= 0 && lowerMark[i] < upperMark[i]);
return ans;
}
};
3. 使矩阵满足条件的最少操作次数
给你一个大小为 m x n 的二维矩形 grid 。每次 操作 中,你可以将 任一 格子的值修改为 任意 非负整数。完成所有操作后,你需要确保每个格子 grid[i][j] 的值满足:
- 如果下面相邻格子存在的话,它们的值相等,也就是
grid[i][j] == grid[i + 1][j](如果存在)。 - 如果右边相邻格子存在的话,它们的值不相等,也就是
grid[i][j] != grid[i][j + 1](如果存在)。
请你返回需要的 最少 操作数目。
示例 1:
输入: grid = [[1,0,2],[1,0,2]]
输出: 0
解释:

矩阵中所有格子已经满足要求。
示例 2:
输入: grid = [[1,1,1],[0,0,0]]
输出: 3
解释:
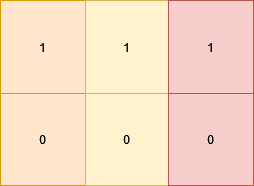
将矩阵变成 [[1,0,1],[1,0,1]] ,它满足所有要求,需要 3 次操作:
- 将
grid[1][0]变为 1 。 - 将
grid[0][1]变为 0 。 - 将
grid[1][2]变为 1 。
示例 3:
输入: grid = [[1],[2],[3]]
输出: 2
解释:

这个矩阵只有一列,我们可以通过 2 次操作将所有格子里的值变为 1 。
提示:
1 <= n, m <= 10000 <= grid[i][j] <= 9
根据题目的描述,我们可以把题目转换为更清晰明了的约束:
- 每一列值必须相同
- 相邻两列值必须不同
那么不受约束的列应该是最右边那一列,它的选择将作为初始约束一直链式约束到第一列,至于每一列调整成哪个数,那当然是看每一列哪个数出现的次数最多,那么剩下需要调整为众数的位置就越少,需要花费的调整次数就越少。不过这是一种贪心的想法,本题能用贪心吗?简单思考一下,如果第一列选择了它那列最优的数字导致第二列不能选某个数字进而导致第三列不能选到最优选择,进而导致非常多后续的列都无法选择到最优数,这是得不偿失的,因此我们没有办法证明这种贪心思路是正确的,只能每列都尝试一遍哪个数会导致总体最优的结果。由于最右边的列是不受约束的,因此 DFS 自然是从最右边的列开始了。
统计各列出现的数的次数,然后 DFS 回溯的时候 记录/消除 本列已选择数的状态,把每一列的每个数都尝试一遍,累积每一列的修改次数,完成最后一列修改之后和最小值比较维护更新。
class Solution {
private:
int m; // row
int n; // col
vector<unordered_map<int, int>> colNumCnt;
vector<int> colChoice; // choice of each column
int ans;
private:
void dfs(int colIdx, const int& tmp) {
// will dfs 1000 level at most (equal to the number of column)
if (colIdx < 0) {
ans = min(ans, tmp);
return;
}
if (tmp >= ans)
return; // no need to dfs more
for (auto [k, v] : colNumCnt[colIdx]) {
colChoice[colIdx] = k;
if (colIdx < n - 1 && colChoice[colIdx] == colChoice[colIdx + 1])
continue;
else
dfs(colIdx - 1, tmp + m - v);
colChoice[colIdx] = -1;
}
}
public:
int minimumOperations(vector<vector<int>>& grid) {
// some initializations
m = grid.size();
n = grid[0].size();
colNumCnt = vector<unordered_map<int, int>>(n);
colChoice = vector<int>(n, -1);
ans = INT_MAX;
// ensurance, incase that each col just have 1 kind of digit
for (int j = 0; j < n; ++j)
for (int k = 0; k < 10; ++k)
colNumCnt[j][k] = 0;
// record times of each digit in each column
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
colNumCnt[j][grid[i][j]]++;
}
}
// dfs
dfs(n - 1, 0);
return ans;
}
};
发现会超时,所以这题没有继续做下去了,当时就感觉是 DP 了,因为能 完全遍历DFS 的情况很多时候都能用 DP 替代。竞赛结束之后看了看交流区的题解,确实是 动态规划 ,并且也不是很难的动态规划。因为调整结束后,每一列的值一定相同,所以动态规划的单词操作就是把一整列赋值为某个值使得子问题的解最优。定义 d p [ i ] [ j ] dp[i][j] dp[i][j] 为计算到第 i i i 列时,前一列选择数为 j j j 的时候具有的最小值, j ∈ [ 0 , 9 ] j \in [0,\ 9] j∈[0, 9] ,因此 d p [ i ] [ j ] dp[i][j] dp[i][j] 所依赖的子问题就是 d p [ i − 1 ] [ 0 ] , … , d p [ i − 1 ] [ 9 ] dp[i-1][0],\ \dots,\ dp[i-1][9] dp[i−1][0], …, dp[i−1][9] 了,因此当前问题依赖的子问题全部属于相邻的上一列,则二维的动态规划矩阵可以使用滚动数组来实现空间复杂度的优化。枚举当前列选择各个数字 [ 0 , 9 ] [0,\ 9] [0, 9] ,通过依赖上一列子问题来求解出每个枚举的最优解,当前调整次数即:上一列调整次数+当前列枚举的数所需剩余调整次数。
class Solution {
public:
int minimumOperations(vector<vector<int>>& grid) {
int m = grid.size(); // m rows
int n = grid[0].size(); // n cols
vector<int> dpcurr(10); // must pre-initialized
vector<int> dpprev(10); // must pre-initialized
vector<int> colcnt(10); // must pre-initialized
for (int col = n-1; col >= 0; --col) {
dpcurr = vector<int>(10, 1<<31-1);
colcnt = vector<int>(10, 0);
for (int row = 0; row < m; ++row)
colcnt[grid[row][col]]++;
for (int i = 0; i < 10; ++i) {
for (int j = 0; j < 10; ++j) {
if (i ^ j) {
dpcurr[i] = min(dpcurr[i], dpprev[j] + m - colcnt[i]);
}
}
}
dpprev = dpcurr;
}
return *std::min_element(dpprev.begin(), dpprev.end());
}
};
4. 最短路径中的边
给你一个 n 个节点的无向带权图,节点编号为 0 到 n - 1 。图中总共有 m 条边,用二维数组 edges 表示,其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。
对于节点 0 为出发点,节点 n - 1 为结束点的所有最短路,你需要返回一个长度为 m 的 boolean 数组 answer ,如果 edges[i] 至少 在其中一条最短路上,那么 answer[i] 为 true ,否则 answer[i] 为 false 。
请你返回数组 answer 。
注意,图可能不连通。
示例 1:

输入: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]
输出: [true,true,true,false,true,true,true,false]
解释:
以下为节点 0 出发到达节点 5 的 所有 最短路:
- 路径
0 -> 1 -> 5:边权和为4 + 1 = 5。 - 路径
0 -> 2 -> 3 -> 5:边权和为1 + 1 + 3 = 5。 - 路径
0 -> 2 -> 3 -> 1 -> 5:边权和为1 + 1 + 2 + 1 = 5。
示例 2:
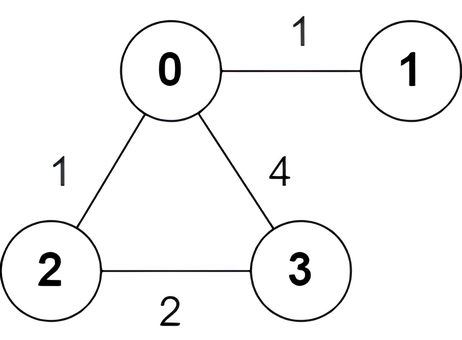
输入: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]
输出: [true,false,false,true]
解释:
只有一条从节点 0 出发到达节点 3 的最短路 0 -> 2 -> 3 ,边权和为 1 + 2 = 3 。
提示:
2 <= n <= 5 * 10^4m == edges.length1 <= m <= min(5 * 10^4, n * (n - 1) / 2)0 <= ai, bi < nai != bi1 <= wi <= 10^5- 图中没有重边。
早知道第四题这么简单就不去死磕第三题了,第三题卡了我半天 DFS 结果还只能过一半的用例。第四题没什么特殊技巧,就是使用迪杰斯特拉记录单源最短路径(多条)然后记录每个节点的来向父节点,最后从终点回溯到起点顺便把经过的边记录到哈希表中以供查询即可。
需要注意的是迪杰斯特拉的设计方式,因为普通的迪杰斯特拉模板只是计算单源最短路径(单个节点到其他节点)的权值之和,但是并不会记录路径,所以必须额外开一个父节点数组,记录每个节点在 迪杰斯特拉BFS 过程中最短路径上的父节点是谁,这样方便后续能从终点回溯到起点。当记录每个节点的路径父节点时需注意,如果多条路径在不同时刻到达同一个节点,且到达时所花费的路径权值之和相同,则无需再将该节点重复入队,否则试想当一个节点被成千上万个节点相连时,每条达到该节点处的路径都将重复的将该节点入队,这是没必要的,因为第一条来到该节点的路径已经负责把该节点入队了,其他到达该节点的路径只需要负责记录路径父节点关系,无需重复将该节点入队,否则当图的边是比较稠密的时候,时间复杂度会大大增加。因此我们在将一个节点入队的时候需要判断到达此节点的路径目前权值之和:
- 更小,我们找到了一条更短的路径,这条路径的父节点关系应该覆盖掉之前已经存在的父节点关系
- 相等,我们找到了一条额外的路径,这条路径的父节点关系应该添加到之前已经存在的父节点关系
- 更大,什么也不做
class Solution {
public:
vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
unordered_map<int, unordered_map<int, int>> graph;
for (const vector<int>& edge : edges) {
graph[edge[0]][edge[1]] = edge[2];
graph[edge[1]][edge[0]] = edge[2];
}
// perform dijkstra once to find all shortest path
vector<vector<int>> parent(n);
vector<int> dist(n, INT_MAX);
queue<pair<int, int>> dijkstraQ;
dist[0] = 0;
dijkstraQ.emplace(0, dist[0]);
while (!dijkstraQ.empty()) {
auto [curr, cdst] = dijkstraQ.front();
dijkstraQ.pop();
for (auto [next, ewgh] : graph[curr]) {
int ndst = cdst + ewgh;
if (ndst <= dist[next]) {
if (ndst < dist[next]) {
dist[next] = ndst;
parent[next].clear();
dijkstraQ.emplace(next, ndst);
}
parent[next].emplace_back(curr);
}
}
}
// restore path from parent relationship
unordered_map<int, unordered_map<int, bool>> valid;
vector<bool> rvSeen(n, false);
queue<int> backtrackQ;
backtrackQ.emplace(n-1);
rvSeen[n-1] = true;
while (!backtrackQ.empty()) {
int curr = backtrackQ.front();
backtrackQ.pop();
for (const int& next : parent[curr]) {
valid[curr][next] = true;
valid[next][curr] = true;
if (rvSeen[next]) continue;
rvSeen[next] = true;
backtrackQ.emplace(next);
}
}
vector<bool> ans(edges.size(), false);
for (int i = 0; i < edges.size(); ++i) {
const vector<int>& edge = edges[i];
if (valid[edge[0]][edge[1]] || valid[edge[1]][edge[0]])
ans[i] = true;
}
return ans;
}
};
注意通过从终点回溯到起点来从父节点关系恢复边关系的时候,也是一样存在前文提到的多条可能路径访问到同一个节点是否要重复入队的问题,因为一条边我们只需要经过一次即可恢复,那么多条可能的路径回溯的时候在不同时刻回到同一节点,当然是只需要第一时刻回溯到该节点的路径负责入队该节点来扩散之后的回溯(也就是使得后续的 BFS 只生效一次),其他后续时刻到来的路径探测只需要恢复与该节点的边关系即可了(如果还入队该节点那么后续的 BFS 会重复执行多次,没必要)。
另外对于只有正边权值的图,进行迪杰斯特拉 BFS 的时候,无需额外的维护一个 “已访问” 节点变量,可以通过到达节点的路径的权值之和判断一个节点是否是回头路,如果绕回头路到达一个节点那么权值之和肯定大于节点已经记录在案的最短距离,因此:
- 新路径权值之和小于节点记录的距离:入队,此时 迪杰斯特拉BFS 对每个节点只计算一条最短路径,尽管可能存在多条同样距离的最短路径
- 新路径权值之和小于等于节点记录的距离:入队,此时 迪杰斯特拉BFS 对每个节点计算多条最短路径,如果存在多条同样距离的最短路径
最后的边是否存在于最短路径上的判断,我一开始还很天真的想用 unordered_map<pair<int, int>, bool> 发现不行,这个 pair<int, int> 默认没有重载哈希。但是 pair<int, int> 是标准库实现了比较运算的,因此可以使用基于红黑树的 set<pair<int, int>> 来做查询。我试了一下,用哈希表的空间占用是 290MB ,用红黑树的空间占用是 216MB。
// restore path from parent relationship
set<pair<int, int>> valid;
vector<bool> rvSeen(n, false);
queue<int> backtrackQ;
backtrackQ.emplace(n-1);
rvSeen[n-1] = true;
while (!backtrackQ.empty()) {
int curr = backtrackQ.front();
backtrackQ.pop();
for (const int& next : parent[curr]) {
valid.emplace(curr, next);
valid.emplace(next, curr);
if (rvSeen[next]) continue;
rvSeen[next] = true;
backtrackQ.emplace(next);
}
}
vector<bool> ans(edges.size(), false);
for (int i = 0; i < edges.size(); ++i) {
const vector<int>& edge = edges[i];
if (valid.count(pair<int, int>(edge[0], edge[1])) || valid.count(pair<int, int>(edge[1], edge[0])))
ans[i] = true;
}



![[数字人]唇形驱动,不生成头部动作算法总结](https://img-blog.csdnimg.cn/direct/ae77ad70a10c45bda8d71267e1298843.png)