【数学建模】优劣解距离法Topsis模型（含MATLAB代码）

news2024/9/20 3:33:44

TOPSIS法，全称 Technique for Order Preference by Similarity to an Ideal Solution，是由C.L.Hwang和K.Yoon于1981年首次提出的 。这是一种多目标决策分析中常用的有效方法，也被称作优劣解距离法 。 TOPSIS法的基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序。如果一个方案距离理想最优解越近，距离最劣解越远，我们就认为这个方案更好 。

TOPSIS法的主要适用场景包括：

土地利用规划：在土地资源管理和规划中，TOPSIS法可以用来评估不同土地利用方案的优劣，帮助决策者选择最佳的土地利用策略 。

物料选择评估：在供应链管理和物料采购中，TOPSIS法可以用来评估不同供应商提供的物料质量，帮助企业选择性价比最高的物料 。

项目投资：在金融管理和投资决策中，TOPSIS法可以用来评估不同投资项目的风险和收益，帮助投资者选择最有利的投资方案 。

医疗卫生：在医疗管理和健康政策制定中，TOPSIS法可以用来评估不同治疗方案的效果，帮助医生和患者选择最佳的治疗方案。

指标类型：

极大型（效益型）期望取值越大越好
极小型期望取值越小越好
中间型期望取值为适当的中间值最好
区间型期望取值落在某一个确定的区间内最好

一致化处理（正向化）：所谓一致化处理就是将评价指标的类型进行统一；使得表中任意属性下性能越优的方案变换后的属性值越大（极大型）。

无量纲化处理：不同指标，不同单位。

归一化：不同指标，不同数值大小。

构造计算评分公式：

TOPSIS法符号说明：

设：多属性决策方案集A={a1，a2，……，am}，即有m个可行方案；

  衡量方案优劣的属性变量（指标）为x1，x2，……，xn，即有n个评价指标这时方案集A中的方案ai（i=1，2，……，m）的n个属性值构成了向量[ai1,ai2,……,ain]它作为n维空间中的一个点，则每个方案依照其各项指标的值就对应n维空间中一个坐标点。

举个栗子：以下是五所高校（ai）的基本情况，我们要根据“人均专著”（x1）、“逾期毕业率”（x2）两个方面来为这五所高校进行一个排名。

序号人均专著/（本/人）逾期毕业率/%
10.14.1
20.35.1
30.46.8
40.80.3
51.21.7

正理想解C+是设想各指标属性都达到最满意值的解[1.2,0.3]

负理想解C-是设想各指标属性都达到最不满意值的解 [0.1,6.8]

在n维空间中，算出方案集D中的各备选方案ai与正理想解C+和负理想解C-的距离：

d*：备选方案di（i=1，2，……，m）到正理想解的距离；

d-：备选方案di（i=1，2，……，m）到负理想解的距离。

理论介绍：

第一步：将n个评价指标x1，x2，……，xn，看成n条坐标轴，由此可以构造出一个n维空间，则每个方案依照其各项指标的数据就对应n维空间中每一个坐标点。

第二步：针对各项指标从所有待评价方案中选出该指标的最优值（正理想解，对应最有坐标点）和最差值（负理想解，对应最差标点），依次求出各个待评价方案的坐标点分别最优坐标点和最差坐标点的距离d*和d-。

第三步：构造相对贴进度（评价参考值）f：

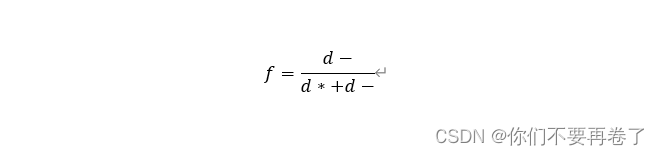
则f值越大代表评价结果越优。

算法步骤：

（1）构造决策矩阵A=(aij)m×n，每一列是一个评价指标，每一行是一个待评价方案；

为了去掉量纲的影响，为了方便比较，做规范化处理得到B=(bij)m×n,其中：

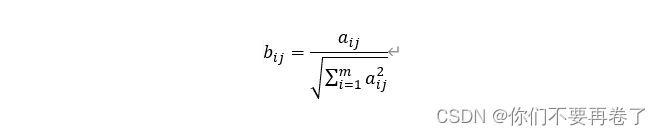
注：该规范化（向量归一化法）处理后，各评价方案的同一评价指标的平方和为1.

（2）根据每个评价指标对评价结果的贡献程度不同，指定不同的权重：

W=[w1,w2,……,wn]，将B的第j列乘以其权重wj，得到带权的规范矩阵C=(cij)m×n。

（3）确定正理想解C+和负理想解C-：

C+=[c1+,c2+,……,cn+];C-=[c1-,c2-, ……,cn-];

（4）计算每个待评价方案到正理想解和负理想解的距离：

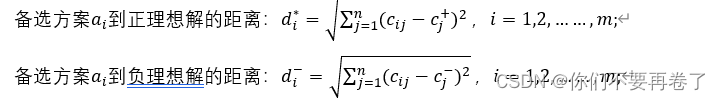 （5）计算每个待评价方案的相对贴进度（评价参考值）：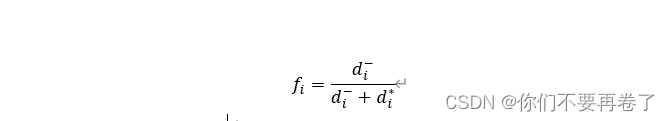

再将从大到小排列 ，得到各备选方案的优先序。

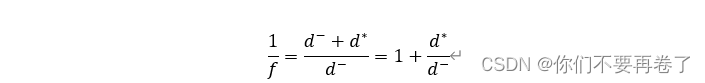
案例分析：以下是五所高校的基本情况，我们要根据“人均专著”、“师生比”、“科研经费”、“逾期毕业率”四个方面围着五所高校进行一个评估。

序号人均专著/（本/人）师生比科研经费/（万元/年）逾期毕业率/%
10.1450004.1
20.3570005.1
30.4960006.8
40.811100002.6
51.228001.7

第一步：导入数据、数据预处理、构建决策矩阵

先把数据规范化，规范化的作用：

a.正向化  b.无量纲化  c.归一化

方法

法1.线性变换法：将原始决策矩阵A =(aij)m×n，进行线性比例变换

    若x为极大型（效益型）属性：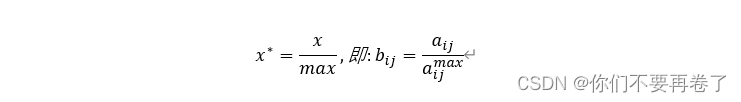

    若x为极小型（成本型）属性：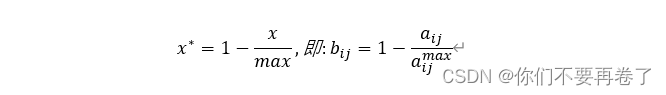 

注：经过该变换之后的bij最优值不一定是1，最差值不一定为0.

0<=bij<=1；所有指标均为正向指标。

法二、极差变换法（使变换后的每个属性的最优值为1，最差为0）

          若x为极大型（效益型）属性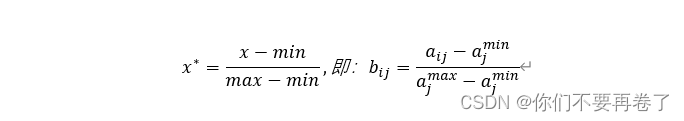：          若x为极小型（成本型）属性：

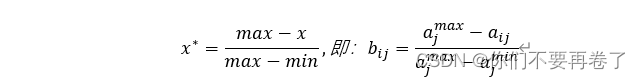
法三、区间型属性的变换：若x区间型属性

           假设给定最优属性区间为[c,d]， 为无法容忍下限，为无法容忍下限

若以该案列为例：假设2某地高校师生比的最有区间为[5,9]，且a2-=1；a2*=12.

序号师生比
14
25
39
411
52

数据处理——>

序号师生比变换后的师生比
140.75
251
391
4110.3333333
520.25

法四、中间属性的变换

           若x为中间型属性，且假设最优值为k，那么：

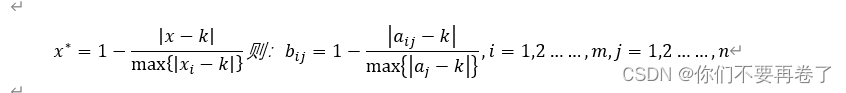 比如：

生产线零件长/cm
112
211
313
415

假设零件在12cm为最佳，则处理后的矩阵为

生产线零件长/cm变换后的零件长/cm
1121
2111/3
3132/3
4150

法五、向量归一化（使得每列平方和为1）

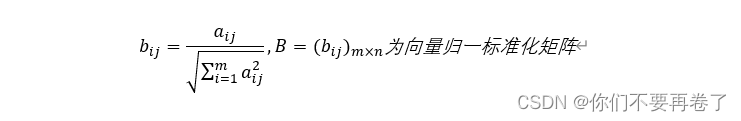 注：向量归一标准化后：

1、0<=bij<=1;

2、正、负向指标的方向没有发生变化

法六、标准样本变换法（大数定律）：

 

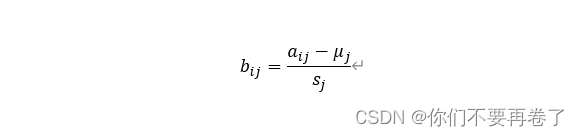
序号人均专著/（本/人）师生比科研经费/（万元/年）逾期毕业率/%
10.1450004.1
20.3570005.1
30.4960006.8
40.811100002.6
51.228001.7

称B=(bij)m×n 为向量标准样本变换矩阵。

注：经标准样本变换后标准化矩阵的样本均值为0，方差为1.

先对第二列进行区间型属性的变换，再对所有属性进行规范化（向量归一法）

序号人均专著/（本/人）师生比科研经费/（万元/年）逾期毕业率/%
10. 0653720450.453413450.3445082140.412670364
20. 1961161350.6045512660. 48231150.513321672
30. 261488180.6045512660. 4134098570.684428896
40. 522976360.2015170890. 6890164280.261693401
50. 7844645410.151137817 0. 055121314 0.171107224

 

确定正理想解和负理想解

正理想解C+=[0.235339362,0.1209102531,0.275606571,0.017110722]

负理想解C-=[0.019611614,0.030227563,0.022048526,0.06844289]

计算各方案到正理想解和负理想解的距离

d*：备选方案ai（i=1，2，……，m）到正理想解的距离；

d-：备选方案ai（i=1，2，……，m）到负理想解的距离

序号d*d-
10.2588927190.133388582
20.1978920460.198124257
30. 1985039370. 179510995
40. 112842220. 291592888
50. 2692861540. 22175088

计算各方案的相近贴进度 

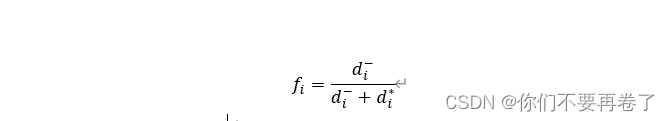
序号fi排行
40.720988071
20.5002931842
30.4748780533
50.4515970594
10.3400329855

 在实际应用中，TOPSIS法因其简便、直观和易于理解的特性，已经被广泛应用于各个领域。然而，需要注意的是，TOPSIS法也有其局限性，比如对数据敏感性高、对样本容量的要求、以及对权重确定的主观性等问题 。因此，在使用TOPSIS法时，应结合实际情况和具体需求，合理考虑其适用性和局限性.

看代码部分：

%%  第一步：把数据复制到工作区，并将这个矩阵命名为X
% （1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
% （2）在Excel中复制数据，再回到Excel中右键，点击粘贴Excel数据（Ctrl+Shift+V）
% （3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）
% （4）注意，代码和数据要放在同一个目录下哦，且Matlab的当前文件夹也要是这个目录。
clear;clc
load data_water_quality.mat
%% 注意：如果提示: 错误使用 load，无法读取文件 'data_water_quality.mat'。没有此类文件或目录。
% 那么原因是因为你的Matlab的当前文件夹中不存在这个文件
% 可以使用cd函数修改Matlab的当前文件夹
% 比如说，我的代码和数据放在了: D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据
% 那么我就可以输入命令：
% cd 'D:第2讲.TOPSIS法（优劣解距离法）\代码和例题数据'
% 也可以看我更新的视频：“更新9_Topsis代码为什么运行失败_得分结果怎么可视化以及权重的确定如何更加准确”，里面有介绍

%%  第二步：判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end

%% 第三步：对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

%% 第四步：计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% A = magic(5)  % 幻方矩阵
% M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
% sort(A)若A是向量不管是列还是行向量，默认都是对A进行升序排列。sort(A)是默认的升序，而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵，默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数：sort（A），排序是按升序进行的，其中A为待排序的向量；
% 若欲保留排列前的索引，则可用 [sA,index] = sort(A,'descend') ，排序后，sA是排序好的向量，index是向量sA中对A的索引。
% sA  =  8     3     2     1
% index =  4     3     1     2

% % 注意：代码文件仅供参考，一定不要直接用于自己的数模论文中
% % 国赛对于论文的查重要求非常严格，代码雷同也算作抄袭
% % 视频中提到的附件可在售后群（购买后收到的那个无忧自动发货的短信中有加入方式）的群文件中下载。包括讲义、代码、我视频中推荐的资料等。
% % 关注我的微信公众号《数学建模学习交流》，后台发送“软件”两个字，可获得常见的建模软件下载方法；发送“数据”两个字，可获得建模数据的获取方法；发送“画图”两个字，可获得数学建模中常见的画图方法。另外，也可以看看公众号的历史文章，里面发布的都是对大家有帮助的技巧。
% % 购买更多优质精选的数学建模资料，可关注我的微信公众号《数学建模学习交流》，在后台发送“买”这个字即可进入店铺(我的微店地址：https://weidian.com/?userid=1372657210)进行购买。
% % 视频价格不贵，但价值很高。单人购买观看只需要58元，三人购买人均仅需46元，视频本身也是下载到本地观看的，所以请大家不要侵犯知识产权，对视频或者资料进行二次销售。
% % 如何修改代码避免查重的方法：https://www.bilibili.com/video/av59423231（必看）

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1612995.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Abaqus python二次开发2-扭转弹簧刚度计算

Abaqus python二次开发2-扭转弹簧刚度计算

Abaqus python二次开发2-扭转弹簧刚度计算 1、定义弹簧参数2、绘制弹簧2.1、绘制弹簧截面2.12、绘制弹簧实体part&#xff08;螺旋旋转截面&#xff09; 3、设置材料、截面属性、并赋给弹簧&#xff08;set&#xff09;4、创建组件的坐标系、参考点和instance&#xff08;弹簧&…
阅读更多...
政安晨：【Keras机器学习示例演绎】（五）—— 利用视觉变换器进行物体检测

政安晨：【Keras机器学习示例演绎】（五）—— 利用视觉变换器进行物体检测

目录 导言 导入和设置 准备数据集 实施多层感知器&#xff08;MLP&#xff09; 实施补丁创建层 显示输入图像的补丁 实施补丁编码层 构建 ViT 模型 运行实验 评估模型 政安晨的个人主页&#xff1a;政安晨 欢迎 &#x1f44d;点赞✍评论⭐收藏 收录专栏: TensorFlow与…
阅读更多...
4.9 启动系统任务❤❤❤

4.9 启动系统任务❤❤❤

有一些特殊的任务需要在系统启动时执行&#xff0c;例如配置文件加载、数据库初始化等操作。 Spring Boot对此提供了两种解决方案&#xff1a;CommandLineRunner和ApplicationRunner。 CommandLineRunner和ApplicationRunner基本一致&#xff0c;差别主要体现在参数上。 1. Co…
阅读更多...
【Linux】在centos快速搭建K8S1.18集群

【Linux】在centos快速搭建K8S1.18集群

使用 kubeadm 创建集群帮助文档 如果您需要以下几点&#xff0c;该工具是很好的选择&#xff1a;kubeadm 一种简单的方法&#xff0c;让你尝试 Kubernetes&#xff0c;可能是第一次。现有用户自动设置群集并测试其应用程序的一种方式。其他生态系统和/或安装程序工具中的构建…
阅读更多...
sublime text的json快捷键

sublime text的json快捷键

系统 macos 配置 sublime Text->Settings->Key Bindings 效果 可以看到&#xff0c;按&#xff1a;shiftcommandp&#xff0c;会出现快捷键窗口&#xff0c;打pretty&#xff0c;会出现Format JSON&#xff0c;最右侧显示⌘J&#xff0c;说明只需要macos的⌘和J同时按…
阅读更多...
目标检测YOLO数据集的三种格式及转换

目标检测YOLO数据集的三种格式及转换

目标检测YOLO数据集的三种格式 在目标检测领域&#xff0c;YOLO&#xff08;You Only Look Once&#xff09;算法是一个流行的选择。为了训练和测试YOLO模型&#xff0c;需要将数据集格式化为YOLO可以识别的格式。以下是三种常见的YOLO数据集格式及其特点和转换方法。 1. YOL…
阅读更多...
https协议的加密方式详解

https协议的加密方式详解

各位大佬能多多点赞关注评论收藏&#xff0c;球球各位大佬们了&#xff01;&#xff01; &#xff01; 目录 1.为什么要加密&#xff1f; 2.如何加密 1.密钥&#xff08;yue,第四声&#xff09; 2.对称加密 3.非对称加密 4.公证机构 3.总结 1.为什么要加密&#xff1f;…
阅读更多...
【机器学习】朴素贝叶斯解决实际问题

【机器学习】朴素贝叶斯解决实际问题

之前写过这样一道题&#xff1a; 现在换成使用朴素贝叶斯解决这个问题 首先先了解一下朴素贝叶斯 这是之前课本里的笔记记录&#xff1a; 【机器学习笔记】朴素贝叶斯&#xff08;从先验分布到后验分布&#xff09;-CSDN博客 简单的讲解一下这道题需要的知识点 朴素贝叶斯是…
阅读更多...
JVM-垃圾收集算法

JVM-垃圾收集算法

前言 在 Java 中&#xff0c;垃圾收集&#xff08;Garbage Collection&#xff09;是一种自动管理内存的机制&#xff0c;它负责在运行时识别和释放不再被程序使用的内存&#xff0c;从而避免内存泄漏和悬空引用问题。本篇文章将介绍三种常见的垃圾收集算法。 标记-清除&…
阅读更多...
11.接口自动化学习-Yaml学习

11.接口自动化学习-Yaml学习

1.配置文件作用 配置文件项目角度&#xff1a; &#xff08;1&#xff09;现成的应用–第三方组件 mysql–数据库–my.conf tomcat–web服务器–server.xml 修改&#xff1a;连接数/端口 redis–缓存服务器–redis.conf 修改配置 jemeter–压测工具–jemeter.properties–修改…
阅读更多...
tcp网络编程——2

tcp网络编程——2

1.一个服务器只能有一个客户端连接&#xff08;下面代码&#xff09; ​​​​​​​tcp网络编程&#xff08;基础&#xff09;-CSDN博客 2.一个服务器可以有多个客户端连接&#xff08;多线程&#xff09; server端创建多个线程&#xff0c;每个线程与不同的client端建立连…
阅读更多...
【Camera Sensor Driver笔记】一、Sensor基本概念

【Camera Sensor Driver笔记】一、Sensor基本概念

时钟 sensor clock sensor的输入时钟 MCLK 输出时钟&#xff1a; 1. VTPixelClock&#xff1a;会影响sensor内部的帧率、曝光 VTPixelClock(vt_clk)Video Timing Clock, From sensor PLL VTPixelClock Framelengthlines x LinelengthPixelClock x FPS Framelengthlines L…
阅读更多...
数据库主从复制

数据库主从复制

一、主从复制概述 1、介绍&#xff1a; 主从复制是指将主数据库的 DDL 和 DML 操作写入到二进制日志中&#xff0c;将二进制日志传送到从库服务器&#xff0c;然后在从库上对这些日志重新执行&#xff08;重做&#xff09;&#xff0c;从而使得从库和主库的数据保持同步。 M…
阅读更多...
复合机器人在磁钢上下料中的应用及其优势分析

复合机器人在磁钢上下料中的应用及其优势分析

复合机器人是一种集成了移动机器人和工业机器人功能的设备&#xff0c;其独特之处在于拥有“手、脚、眼、脑”的综合能力&#xff0c;从而实现了更高的灵活性和操作效率。在磁钢上下料的应用场景中&#xff0c;复合机器人能够发挥显著的优势。 首先&#xff0c;复合机器人可以根…
阅读更多...
chrome浏览器查看css样式

chrome浏览器查看css样式

样式的查看 1.匹配器为灰色文本&#xff1a; 表示非当前选择器 2.样式有划线标识&#xff1a;CSS属性无效或未知 / 属性值无效 / 被其他属性覆盖的属性 3.属性以浅色文本显示且有感叹号提示&#xff1a;属性虽然有效&#xff0c;但由于CSS逻辑而没有任何影响 转自&#xff1a;…
阅读更多...
判断完数（C语言）

判断完数（C语言）

一、N-S流程图&#xff1b; 二、运行结果&#xff1b; 三、源代码&#xff1b; # define _CRT_SECURE_NO_WARNINGS # include <stdio.h>int main() {//初始化变量值&#xff1b;int n 0;int i 1;int j 0;int result 1;//提示用户&#xff1b;printf("请输入一个…
阅读更多...
Axure如何实现限制选择项数量的交互

Axure如何实现限制选择项数量的交互

大家经常会看到这样的功能设计&#xff1a;可以多选&#xff0c;但是限制多选。比如某招聘网站城市的选择只能选择5个。再选择第6个的时候会提示最多只能选择5项。 这个效果是我们经常会遇到的&#xff0c;在工作中也经常会遇到需要制作这样的效果。今天我们一起来看看&#xf…
阅读更多...
Matlab无基础快速上手1（遗传算法框架）

Matlab无基础快速上手1（遗传算法框架）

本文用经典遗传算法框架模板&#xff0c;对matlab新手友好&#xff0c;快速上手看懂matlab代码&#xff0c;快速应用实践&#xff0c;源代码在文末给出。 基本原理&#xff1a; 遗传算法&#xff08;Genetic Algorithm&#xff0c;GA&#xff09;是一种受生物学启发的优化算法…
阅读更多...
IDEA JAVA项目如何设置JVM参数

IDEA JAVA项目如何设置JVM参数

问题背景&#xff1a; 有时候项目在本地启动时会报参数引用不到&#xff0c;如果确实找不到在哪里添加的话&#xff0c;我们可以先加JVM参数来暂时解决本地环境的调试。 解决方案&#xff1a; 编辑配置Edit Configurations 选择需要配置的项目&#xff0c;点击Modify options 选…
阅读更多...
FileNotFoundError: [Errno 2] No such file or directory: ‘llvm-config‘

FileNotFoundError: [Errno 2] No such file or directory: ‘llvm-config‘

查找本地的llvm-config find / -name llvm-config 2>/dev/null 输出 /usr/local/Cellar/llvm/17.0.6_1/bin/llvm-config 执行安装命令 LLVM_CONFIG/usr/local/Cellar/llvm/17.0.6_1/bin/llvm-config pip install llvmlite # 看自己路径在哪
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023