之前写过这样一道题:
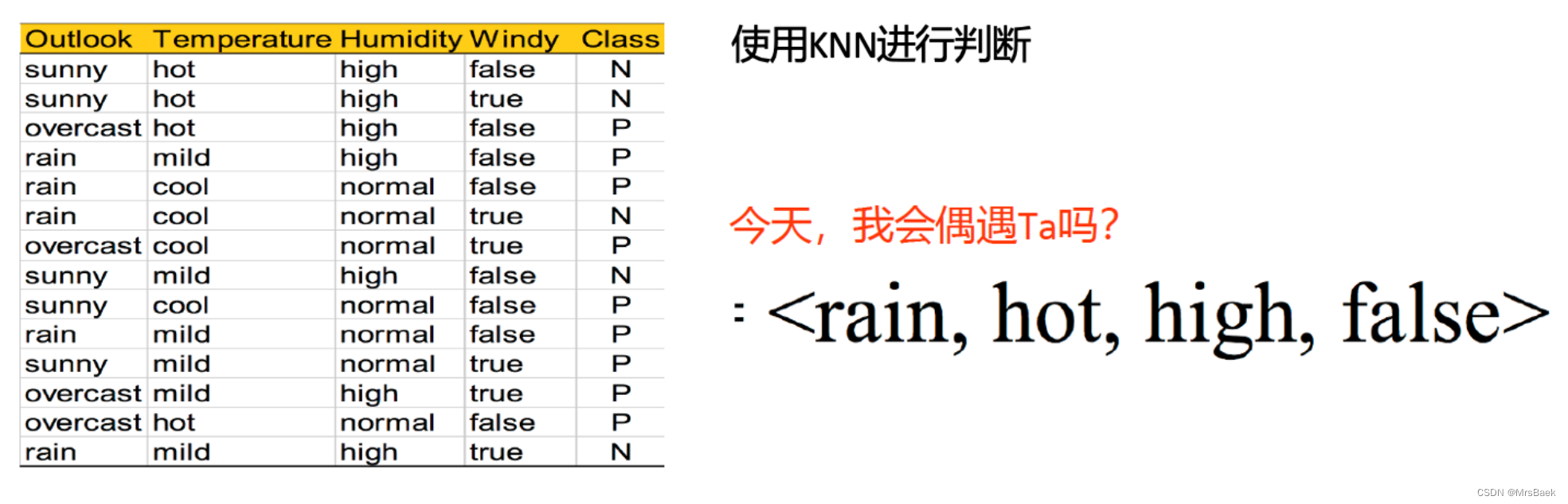
现在换成使用朴素贝叶斯解决这个问题
首先先了解一下朴素贝叶斯
这是之前课本里的笔记记录:
【机器学习笔记】朴素贝叶斯(从先验分布到后验分布)-CSDN博客
简单的讲解一下这道题需要的知识点
朴素贝叶斯是一个基于贝叶斯定理的简单概率分类器,它假设给定目标值时特征之间的条件独立性。"朴素"这个词意味着这个模型在概率模型中忽略了特征之间的相互作用。
它工作的方式如下:
贝叶斯定理: 这是朴素贝叶斯分类器的核心,它提供了给定某个类别下观测到某些特征的概率。公式如下:![]()
在这里 P(A|B) 是在给定 B 的情况下 A 的概率, P(B|A)是在给定 A 的情况下观察到 B 的概率,P(A)和P(B)分别是 A 和 B 的边缘概率。
条件独立性假设: 在给定目标类别的情况下,假设所有特征都是相互独立的。尽管这个假设在实际情况中很少成立,但朴素贝叶斯分类器在实践中表现得出奇地好,即使特征之间存在一定的依赖。
训练: 在训练过程中,分类器会通过数据集计算特征与类别之间的关系,即每个类别下特征的条件概率。
预测: 在预测时,它会使用这些概率和贝叶斯定理来预测未见实例的类别。对于每个类别,它会计算一个概率,并将实例分类到具有最高概率的类别。
朴素贝叶斯分类器适用于多种分类任务,特别是文本分类。因为其计算效率很高,并且易于实现,所以在处理大型数据集时尤其受欢迎。此外,由于其对缺失数据不敏感,它也适用于不完整数据集。
朴素贝叶斯算法是一种基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对于给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。
我们要预测的新实例是:
![]()
对于这个示例,我们要使用朴素贝叶斯算法来预测它是否属于类别N或P。
步骤如下:
1. 数据准备:
数据集由不同天气情况的属性(Outlook, Temperature, Humidity, Windy)和一个类别标签(Class)组成。
LabelEncoder被用来将文本数据转换为模型可以理解的数值数据。

2. 数据转换:
数据集中的每一行都被转换成数值格式,这一过程使用了之前拟合好的编码(`LabelEncoder`)。

3. 模型训练:
创建了GaussianNB分类器实例,并使用特征和对应的标签来训练它。

4. 新数据点的预测:
定义了一个新的数据点,表示今天的天气情况。
使用相同的编码器将新数据点转换为数值。
使用训练好的朴素贝叶斯模型对新数据点的类别进行预测。

5. 解码和输出结果:
使用class_encoder.inverse_transform方法将预测结果从数值转换回原始的类别标签。

根据解码后的标签输出预测结果,即今天是否会遇见所询问的人。
每一步都关键地支持了整个预测流程,确保数据以正确的格式输入模型,并且预测结果以人类可读的形式呈现。你的代码组织得很好,并且包含了从数据准备到结果输出的完整流程。

完整代码如下:
from sklearn.naive_bayes import GaussianNB
from sklearn.preprocessing import LabelEncoder
# 数据准备
data = [
["sunny", "hot", "high", False, "N"],
["sunny", "hot", "high", True, "N"],
["overcast", "hot", "high", False, "P"],
["rain", "mild", "high", False, "P"],
["rain", "cool", "normal", False, "P"],
["rain", "cool", "normal", True, "N"],
["overcast", "cool", "normal", True, "P"],
["sunny", "mild", "high", False, "N"],
["sunny", "cool", "normal", False, "P"],
["rain", "mild", "normal", False, "P"],
["sunny", "mild", "normal", True, "P"],
["overcast", "mild", "high", True, "P"],
["overcast", "hot", "normal", False, "P"],
["rain", "mild", "high", True, "N"]
]
# 转换数据集
outlook_encoder = LabelEncoder().fit(["sunny", "overcast", "rain"])
temperature_encoder = LabelEncoder().fit(["hot", "mild", "cool"])
humidity_encoder = LabelEncoder().fit(["high", "normal"])
windy_encoder = LabelEncoder().fit([False, True])
class_encoder = LabelEncoder().fit(["N", "P"])
numerical_data = []
for row in data:
numerical_row = [
outlook_encoder.transform([row[0]])[0],
temperature_encoder.transform([row[1]])[0],
humidity_encoder.transform([row[2]])[0],
windy_encoder.transform([row[3]])[0],
class_encoder.transform([row[4]])[0]
]
numerical_data.append(numerical_row)
# 分离特征和类别标签
features = [row[:-1] for row in numerical_data]
labels = [row[-1] for row in numerical_data]
# 创建和训练朴素贝叶斯模型
nb = GaussianNB()
nb.fit(features, labels)
# 预测新的数据点
new_point = ["rain", "hot", "high", False]
numerical_new_point = [
outlook_encoder.transform([new_point[0]])[0],
temperature_encoder.transform([new_point[1]])[0],
humidity_encoder.transform([new_point[2]])[0],
windy_encoder.transform([new_point[3]])[0]
]
# 使用朴素贝叶斯进行预测
predicted_class = nb.predict([numerical_new_point])[0]
# 解码预测结果
predicted_label = class_encoder.inverse_transform([predicted_class])[0]
# 根据预测的标签输出结果
if predicted_label == 'P':
print("今天会遇见ta吗: 能")
elif predicted_label == 'N':
print("今天会遇见ta吗: 不能")
这是我的作业啊。。查重率我不怕 仅供学习和记录


![FileNotFoundError: [Errno 2] No such file or directory: ‘llvm-config‘](https://img-blog.csdnimg.cn/direct/ba8556612b334d8c94a656517bf6e4f1.png)


![[数据结构与算法]-什么是二叉树?](https://img-blog.csdnimg.cn/direct/ff30a20a727b44c8a7ff28d35994e478.png#pic_center)