同质图中的注意力网络
注意力网络
GAT 核心就是对于每个顶点都计算其与邻居节点的注意力系数，通过注意力系数来聚合节点的特征，而非认为每个邻居节点的贡献程度都是相同的
单头注意力机制
为了计算注意力权重 eij，我们首先将即节点特征 hi 和 hj 通过 W 映射到一个高维空间，然后将这两个向量拼接在一起，之后通过一个全连接层 afc 将拼接后的向量映射到一个标量，再应用 LeakyReLU 激活函数得到注意力系数 eij
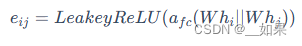，其中afc 的参数是被共享的
假设目标节点 i 有 k 个邻居节点 j，因此我们需要用 softmax 对得到的所有注意力系数进行归一化，就可以用其对邻居节点特征进行线性组合，得到最终的目标节点特征
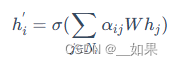
多头注意力机制
使用 K 个 Wk 将原特征进行映射到 K 个不同的高维空间，然后重复上述计算单头注意力的步骤
最后concat或者加权组合起来
注意力网络代码
class GATLayer(nn.Module):
def __init__(self, g, in_dim, out_dim):
super(GATLayer, self).__init__()
'''
g : dgl的grapg实例
in_dim : 节点embedding维度
out_dim : attention编码维度
'''
self.g = g #dgl的一个graph实例
self.fc = nn.Linear(in_dim, out_dim, bias=False) # 对节点进行通用的映射的fc
self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False) # 计算edge attention的fc
self.reset_parameters() # 参数初始化
def edge_attention(self, edges):
'''
edges 的src表示源节点,dst表示目标节点
'''
z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1) # eq.1 里面的拼接操作
a = self.attn_fc(z2) # eq.1 里面对e_{ij}的计算
return {'e' : F.leaky_relu(a)} # 这里的return实际上等价于 edges.data['e'] = F.leaky_relu(a),这样后面才能将这个 e 传递给 源节点
def reset_parameters(self):
gain = nn.init.calculate_gain('relu')
nn.init.xavier_normal_(self.fc.weight, gain=gain)
nn.init.xavier_normal_(self.attn_fc.weight, gain=gain)
def message_func(self, edges):
return {'z' : edges.src['z'], 'e' : edges.data['e']} #将前面 edge_attention 算出来的 e 以及 edges的源节点的 node embedding 都传给 nodes.mailbox
def reduce_func(self, nodes):
# 通过 message_func 之后即可得到 源节点的node embedding 与 edges 的 e
alpha = F.softmax(nodes.mailbox['e'], dim=1) # softmax归一化，得到 a
h = torch.sum(alpha * nodes.mailbox['z'], dim=1) # 根据a进行加权求和
return {'h' : h}
def forward(self, h):
z = self.fc(h) # eq. 1 这里的h就是输入的node embedding
self.g.ndata['z'] = z
self.g.apply_edges(self.edge_attention) # eq. 2
self.g.update_all(self.message_func, self.reduce_func) # eq. 3 and 4
return self.g.ndata.pop('h') # 返回经过attention的 node embedding
class MultiHeadGATLayer(nn.Module):
def __init__(self, g, in_dim, out_dim, num_heads, merge='cat'):
super(MultiHeadGATLayer, self).__init__()
'''
g : dgl的grapg实例
in_dim : 节点embedding维度
out_dim : attention编码维度
num_heads : 头的个数
merge : 最后一层为'mean',其他层为'cat'
'''
self.heads = nn.ModuleList()
for i in range(num_heads):
# 这里简单粗暴，直接声明 num_heads个GATLayer达到 Multi-Head的效果
self.heads.append(GATLayer(g, in_dim, out_dim))
self.merge = merge
def forward(self, h):
head_outs = [attn_head(h) for attn_head in self.heads]
# 根据merge的类别来处理 Multi-Head的逻辑
if self.merge == 'cat':
return torch.cat(head_outs, dim=1)
else:
return torch.mean(torch.stack(head_outs))class GAT(nn.Module):
def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):
super(GAT, self).__init__()
'''
g : dgl的grapg实例
in_dim : 节点embedding维度
hidden_dim : 隐层的维度
out_dim : attention编码维度
num_heads : 头的个数
'''
# 这里简简单单的写了一个两层的 MultiHeadGATLayer
self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)
self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)
def forward(self, h):
h = self.layer1(h)
h = F.elu(h)
h = self.layer2(h)
return h结果可通过 t-SNE 降维来进行可视化
异质图中的注意力网络
异质图注意力网络
元路径及依据元路径定义的邻居
在异质图中会有非常复杂的节点之间的联系，但是这种联系并不全是有效的，所以通过定义元路径来定义一些有意义的连接方式
节点 i 在通过元路径生成的图中的邻居就是依据元路径定义的邻居
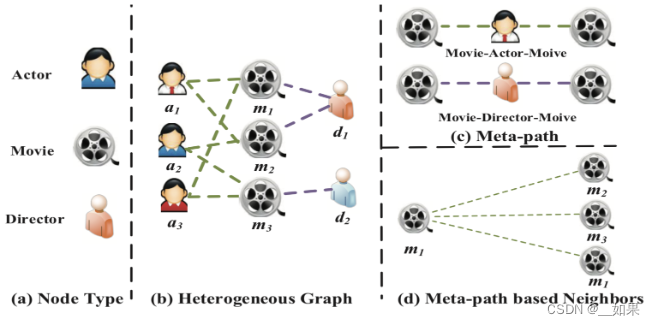
如图元路径可定义为MAM和MDM，便得到了依据元路径定义的邻居d
异质图注意力网络整体架构
- （a）节点级注意力的目的是学习节点与基于元路径的邻居节点之间的重要性。
- （b）语义级注意力的目的是学习不同元路径的重要性。
- （c）通过接
MLP输出节点 i 的预测 y~i。
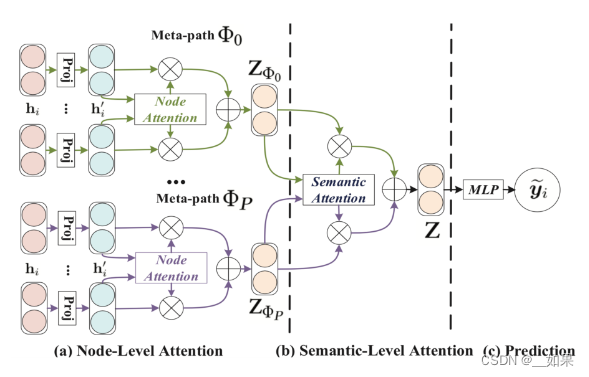
节点级注意力
对每一条元路径形成的邻居节点子图进行一次同质图卷积网络 GAT 的注意力计算
语义级注意力
首先，初始化一个语义级别的可学习向量 q，然后用 q 和每个元路径的节点级特征的高维映射 WZiΦp 求内积，并且平均了所有的节点 i 后，得到元路径 p 的语义级注意力系数
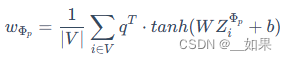
最后对进行softmax归一化后的注意力系数进行加权求和
异质图注意力网络代码
class SemanticAttention(nn.Module):
def __init__(self, in_size, hidden_size=128):
super(SemanticAttention, self).__init__()
self.project = nn.Sequential(
nn.Linear(in_size, hidden_size),
nn.Tanh(),
nn.Linear(hidden_size, 1, bias=False)
)
def forward(self, z):
w = self.project(z).mean(0) # (M, 1)
beta = torch.softmax(w, dim=0) # (M, 1)
beta = beta.expand((z.shape[0],) + beta.shape) # (N, M, 1)
return (beta * z).sum(1) # (N, D * K)
class HANLayer(nn.Module):
"""
HAN layer.
Arguments
---------
num_meta_paths : number of homogeneous graphs generated from the metapaths.
in_size : input feature dimension
out_size : output feature dimension
layer_num_heads : number of attention heads
dropout : Dropout probability
Inputs
------
g : list[DGLGraph]
List of graphs
h : tensor
Input features
Outputs
-------
tensor
The output feature
"""
def __init__(self, num_meta_paths, in_size, out_size, layer_num_heads, dropout):
super(HANLayer, self).__init__()
# One GAT layer for each meta path based adjacency matrix
self.gat_layers = nn.ModuleList()
for i in range(num_meta_paths):
self.gat_layers.append(GATConv(in_size, out_size, layer_num_heads,
dropout, dropout, activation=F.elu))
self.semantic_attention = SemanticAttention(in_size=out_size * layer_num_heads)
self.num_meta_paths = num_meta_paths
def forward(self, gs, h):
semantic_embeddings = []
for i, g in enumerate(gs):
semantic_embeddings.append(self.gat_layers[i](g, h).flatten(1))
semantic_embeddings = torch.stack(semantic_embeddings, dim=1) # (N, M, D * K)
return self.semantic_attention(semantic_embeddings) # (N, D * K)
class HAN(nn.Module):
def __init__(self, num_meta_paths, in_size, hidden_size, out_size, num_heads, dropout):
super(HAN, self).__init__()
self.layers = nn.ModuleList()
self.layers.append(HANLayer(num_meta_paths, in_size, hidden_size, num_heads[0], dropout))
for l in range(1, len(num_heads)):
self.layers.append(HANLayer(num_meta_paths, hidden_size * num_heads[l-1],
hidden_size, num_heads[l], dropout))
self.predict = nn.Linear(hidden_size * num_heads[-1], out_size)
def forward(self, g, h, is_training=True):
for gnn in self.layers:
h = gnn(g, h)
if is_training:
return self.predict(h)
else:
return h
![[阅读笔记29][AgentStudio]A Toolkit for Building General Virtual Agents](https://img-blog.csdnimg.cn/direct/dfeb73e7542148de810cc3ae9d62d93e.png)
