♥♥♥♥♥个人主页♥♥♥♥♥
♥♥♥♥♥数据结构练习题总结专栏♥♥♥♥♥
♥♥♥♥♥上一章：队——1.用队实现栈2.用栈实现队♥♥♥♥♥

1.相同的树

1.1题目描述

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

1.2 思路分析

此题可以采用子问题的方式去解答
基本思想：
只要确定根结点结构上和值都是相同的，后面直接去递归根结点的左右子树即可。

判断根结点的结构与值：
1.结构上：
1.1 一个根结点为空，另一个根结点不为空，则返回false
1.2两个根结点都为空，则返回true
2.结构上相同但根结点的值不同，返回false
3.根结点结构和值都相同，返回true

1.3绘图分析

1.结构上：
1.1 一个根结点为空，另一个根结点不为空：

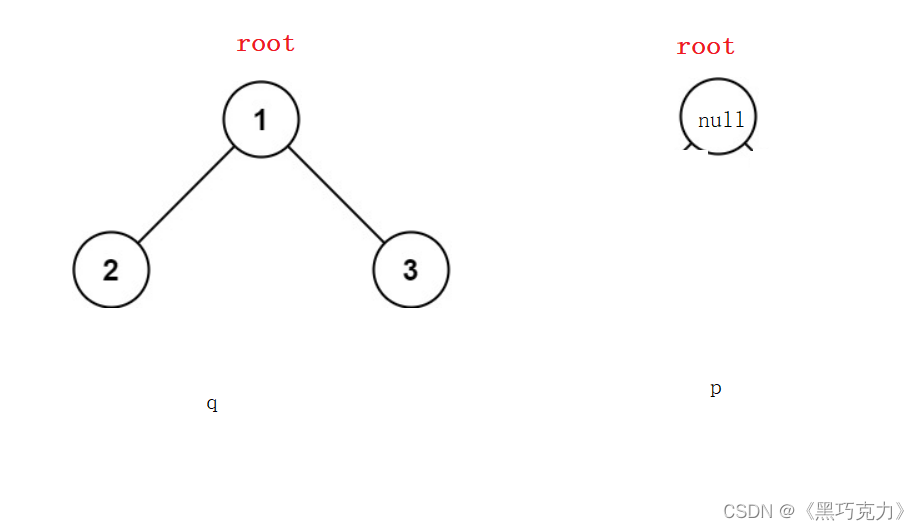
1.2两个根结点都为空：

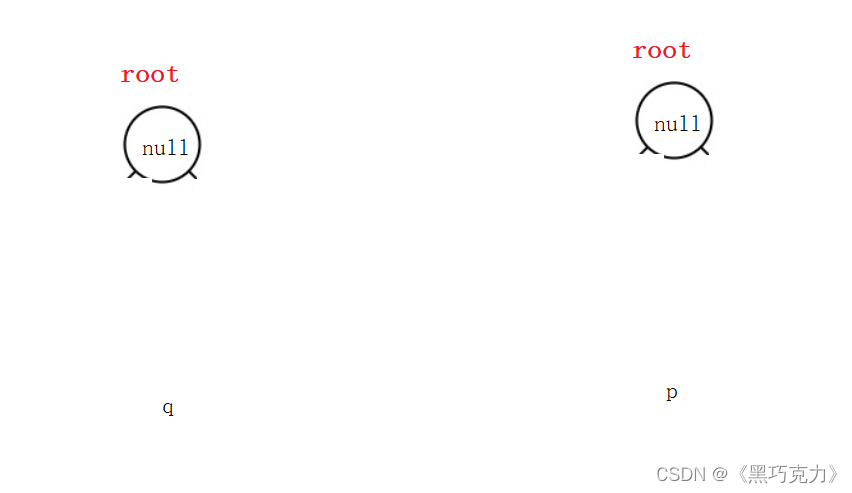
2.结构上相同但根结点的值不同：

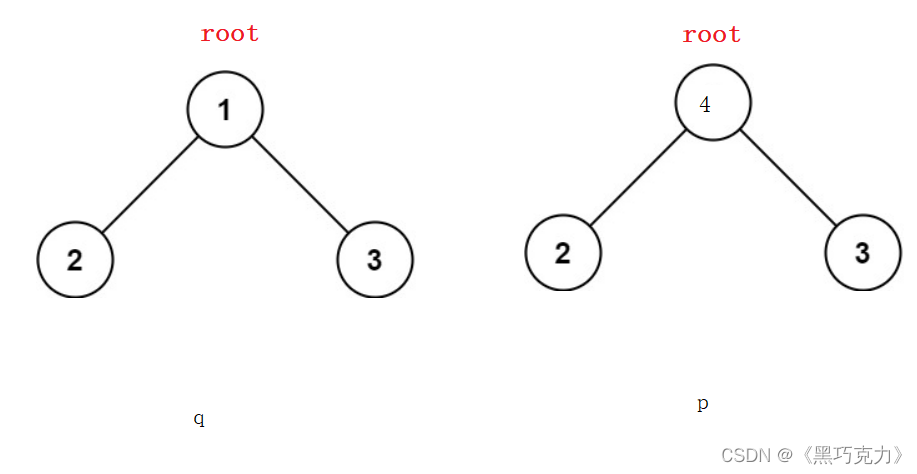
3.根结点结构和值都相同：

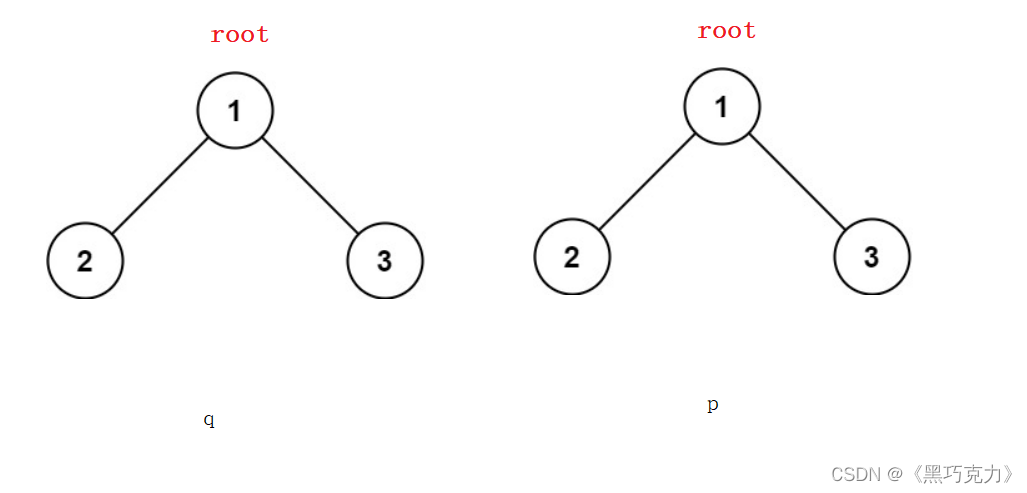
1.4代码实现

//判断相同的树
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //1.结构上

        //1.1 一个根结点为空，另一个不为空
        if(p == null && q != null || p != null && q == null) {
            return false;
        }
        //1.2 两个根结点都为空
        if(p == null && q == null) {
            return true;
        }
        //2.根的值不相同
        if(p.val != q.val) {
            return false;
        }
        //到了这里说明根结点相同并且也相同
        return  isSameTree(p.left,q.left) &&  isSameTree(p.right,q.right);
    }

2.另一颗树的子树

2.1问题描述

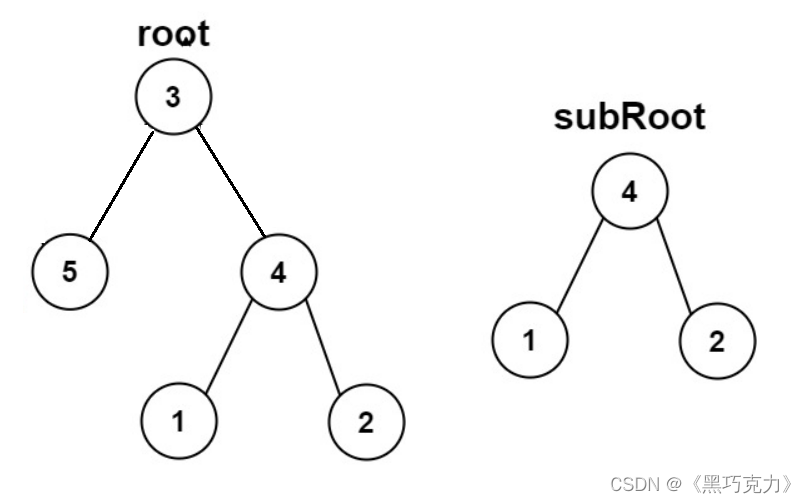
给你两棵二叉树 root 和 subRoot ，检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树，如果存在返回 true 否则返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

2.2思路分析

基本思想：
同样去用子问题的思想去剖析这个问题，先判断这个 subRoot 是不是root的子树，然后再去通过递归的方式判断是不是root左右子树的子树
思路描述：
1.先判断 subRoot 是否为root的子树
2.再去判断 subRoot 是否为root.left的子树
3.最后去判断 subRoot 是否为root.right的子树

2.3绘图分析

1.先判断 subRoot 是否为root的子树：

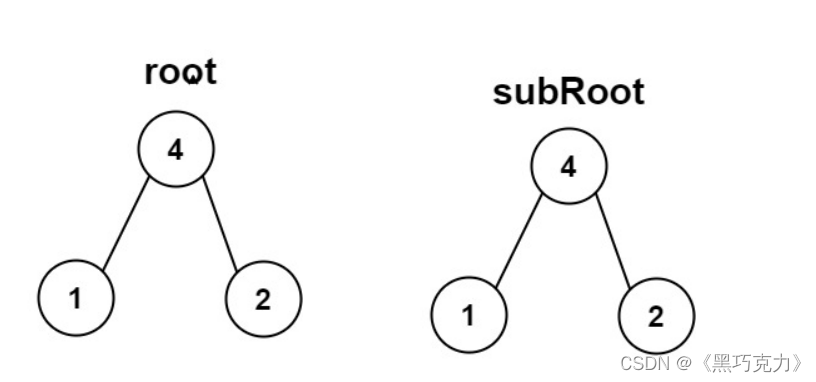
2.再去判断 subRoot 是否为root.left的子树：

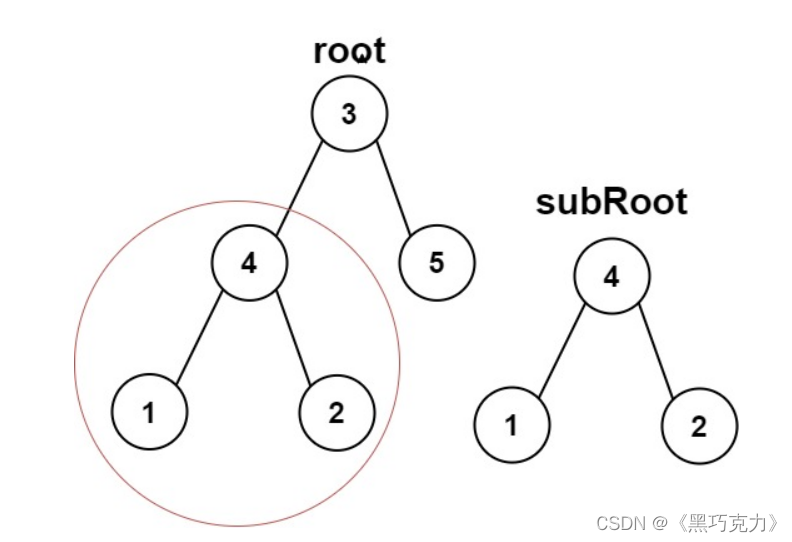
3.最后去判断 subRoot 是否为root.right的子树：

2.4代码实现

public boolean isSameTree(TreeNode p, TreeNode q) {
        //1.结构上

        //1.1 一个根结点为空，另一个不为空
        if(p == null && q != null || p != null && q == null) {
            return false;
        }
        //1.2 两个根结点都为空
        if(p == null && q == null) {
            return true;
        }
        //2.根的值不相同
        if(p.val != q.val) {
            return false;
        }
        //到了这里说明根结点相同并且也相同
        return  isSameTree(p.left,q.left) &&  isSameTree(p.right,q.right);
    }

    //另一棵树的子树
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null) {
            return false;
        }
        if (isSameTree(root, subRoot)) {
            return true;
        }
        if(isSubtree(root.left, subRoot)) {
            return true;
        }
        if(isSubtree(root.right, subRoot)) {
            return true;
        }
        return false;
    }

3.翻转二叉树

3.1问题描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

3.2思路分析

基本思想：子问题分析法

1.先判断根结点是否为空
2.找一个中间结点tmp，通过交换法将root的左右树进行交换
3.递归左右树

3.3绘图分析

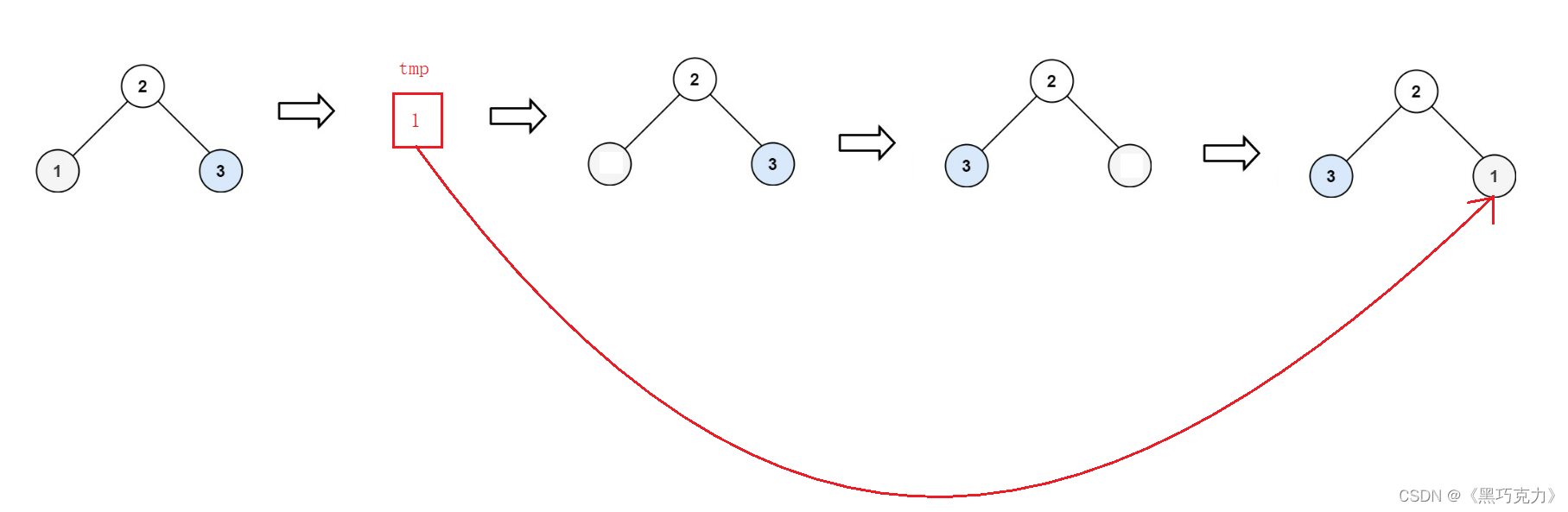
3.4代码实现

//翻转二叉树
    public TreeNode invertTree(TreeNode root) {
        //1.判断根结点
        if(root == null) {
            return null;
        }

        //加一个判断根结点的左右结点是null则直接返回根结点root ，可以减少很多的左右树的递归
        if(root.left == null && root.right == null) {
            return root;
        }

        //定义一个tmp结点，来为root左右结点交换作中间站
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        //递归左右子树
        invertTree(root.left);
        invertTree(root.right);


        return root;
    }

4.平衡二叉树

4.1问题描述

给定一个二叉树，判断它是否是 平衡二叉树(每个结点的左子树和右子树的高度差至多等于1)

4.2思路分析

基本思想：子问题分析
1.先判断根结点是否为空
2.递归左右子树得到左右子树的高度，高度差小于等于1为平衡树则返回树的高度，反之返回-1

4.3绘图分析

1.符合平衡树：

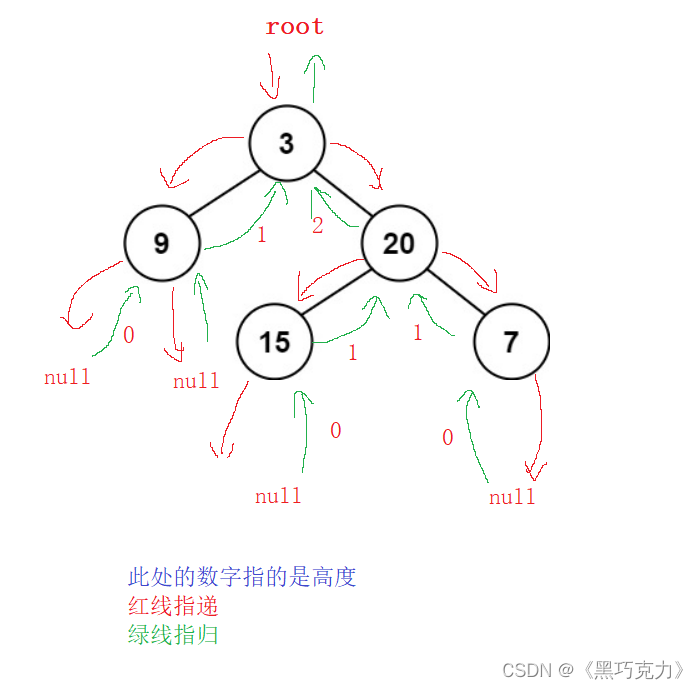
2.不符合平衡树：

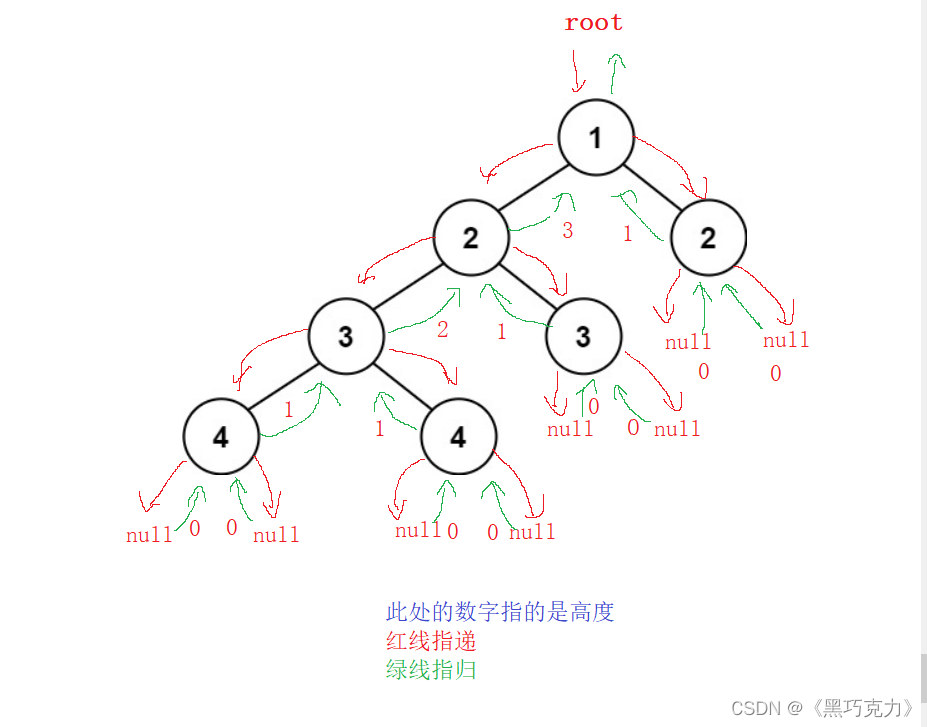
4.4代码实现

 //平衡二叉树  O(n)
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        return getHeight(root)>=0;
    }
    //我们规定一下如果不是平衡树返回负数，是平衡树返回树的高度
    public int getHeight2(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = getHeight2(root.left);
        int rightHeight = getHeight2(root.right);
        if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1)
        {
            return Math.max(leftHeight,rightHeight)+1;
        }
        else {
            return -1;
        }
    }

5.对称二叉树

5.1问题描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

5.2思路分析

基本思想：子问题分析
1.对根结点分析
1.1结构上：
1.1.1左为空右不为空或者左不为空右为空
1.1.2左右都为空
1.2值：
1.2.1左右值都不相同
1.2.2左右值都相同
2.递归左右子树

5.3绘图分析

1.1结构上：
1.1.1左为空右不为空或者左不为空右为空：

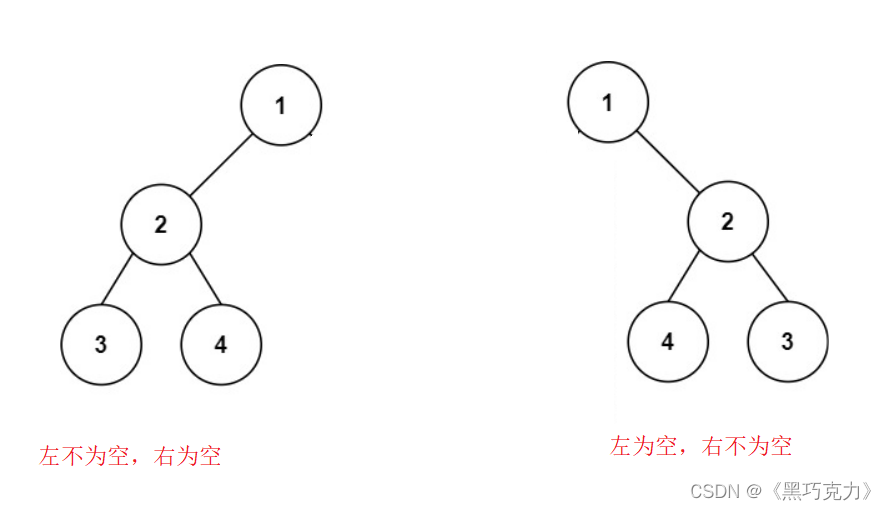
1.1.2左右都为空：

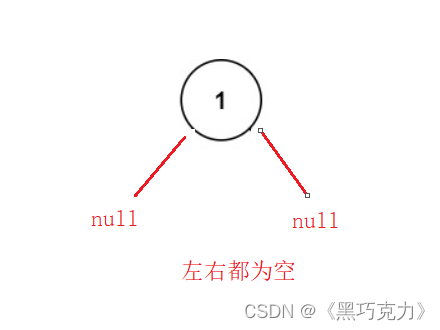
1.2值：
1.2.1左右值都不相同：

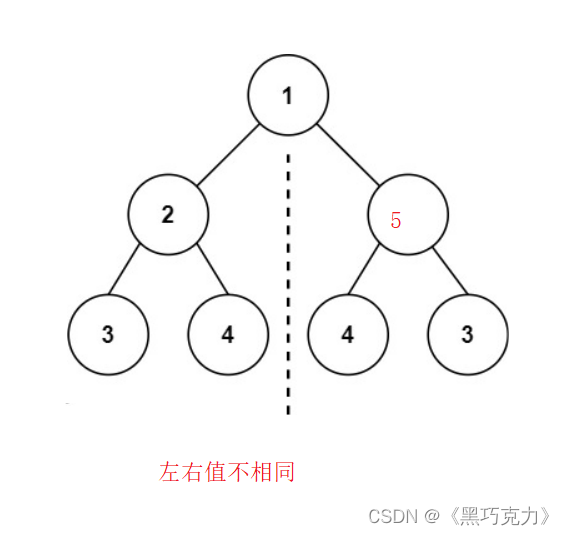
1.2.2左右值都相同：

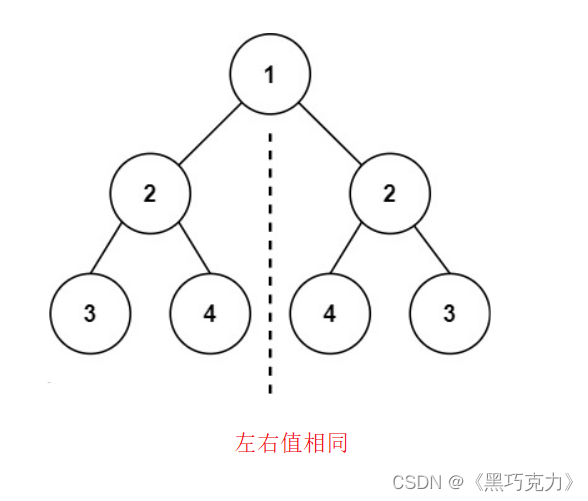
5.4代码实现

//对称二叉树
    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }
        return isSymmetricChild(root.left,root.right);
    }
    public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree) {
        //1.结构上
        //1.1左为空右不为空或者左不为空右为空
        if(leftTree ==null && rightTree!=null || leftTree !=null && rightTree==null) {
            return false;
        }
        //1.2左右都为空
        if(leftTree == null && rightTree == null) {
            return true;
        }
        //2.值
        //2.1左右的值都不相同
        if(leftTree.val != rightTree.val) {
            return false;
        }
        //2.2左右的值都相同
        return isSymmetricChild(leftTree.left,rightTree.right) && isSymmetricChild(leftTree.right,rightTree.left);
    }

结尾：希望大家可以给我点点关注，点点赞，并且在评论区发表你们的想法和意见，我会认真看每一条评论，你们的支持就是我的最大鼓励。🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹