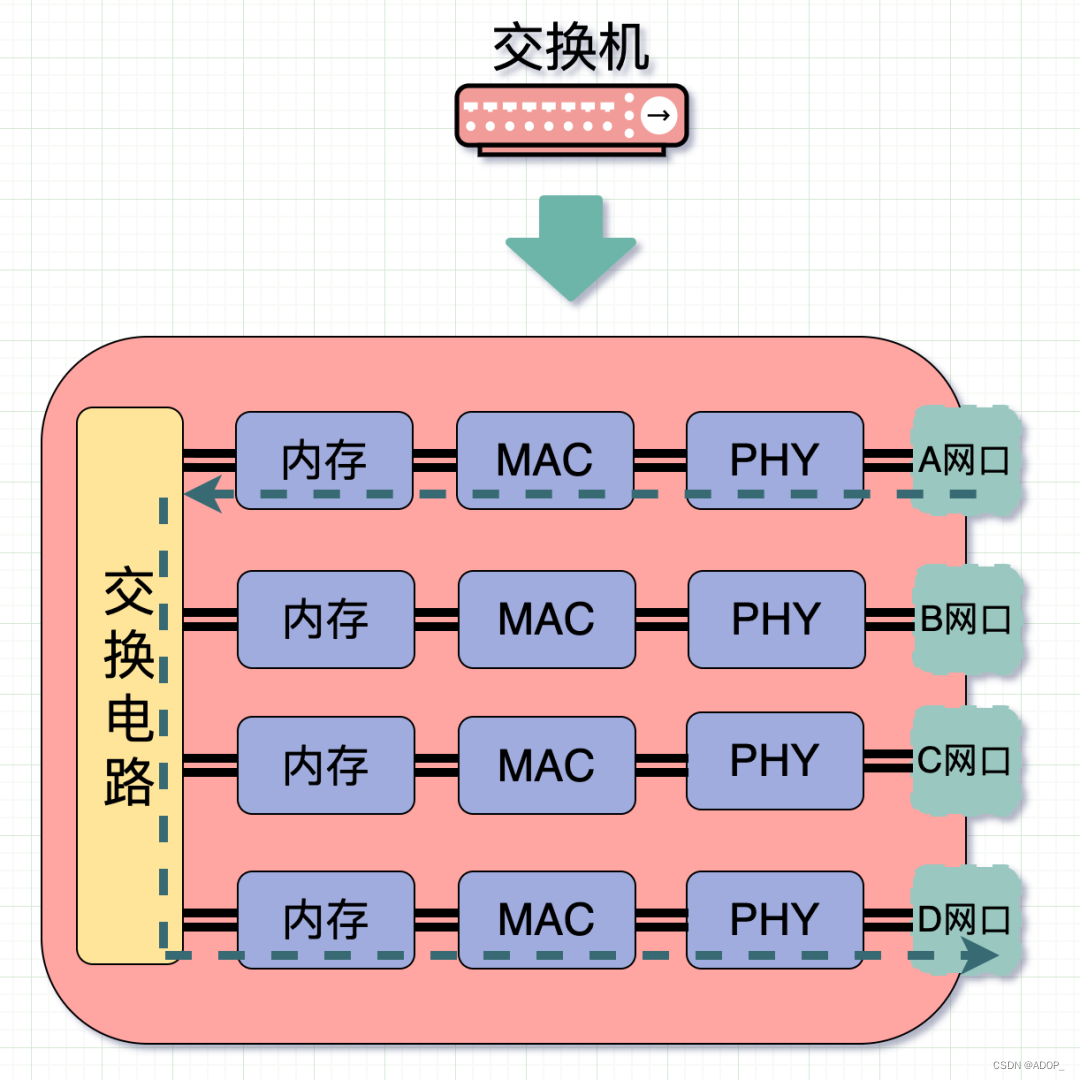
大家好，我是吴军，今天我将与大家探讨一种别具一格的商业模式——循环购模式。或许您曾经听说过消费满额赠送现金的活动，甚至每天都能累积并提取部分现金。您可能会好奇，商家为何如此慷慨地“回馈”消费者？这背后其实蕴含了一种创新的商业逻辑。

循环购模式并非仅仅是资金的回馈，而是一种融合了消费返利与积分机制的新型商业模式。市场上确实存在一些消费返利的欺诈行为，但消费返利模式本身并非问题所在。关键在于如何构建合理的返利机制，既能促进产品销售，又能维护市场的健康发展。

在这种模式下，用户消费后，商家会根据消费额度赠送相应的能量值与贡献值。能量值可以视为一种返现的凭证，而贡献值则决定了用户每日可获得的返现金额。以用户A为例，假设他在循环购平台消费了1000元，那么他将获得相应的能量值和贡献值。根据平台的分红机制，用户A每天都能获得一定比例的返现金额。

具体来说，如果用户A在平台上消费了1000元并获得了相应的能量值和贡献值，这些能量值代表了他可以获得的返现金额的上限，而贡献值则决定了每日的返现比例。假设平台当日总流水为1万元，全网贡献值总和为100个，那么用户A的贡献值占全网的比例将决定他当日能够分得的金额。

此外，循环购模式还可以结合会员制度和团队管理策略，为用户提供更多增加收益的机会。商家也可以通过设置推荐奖励等方式，吸引更多的用户参与进来。

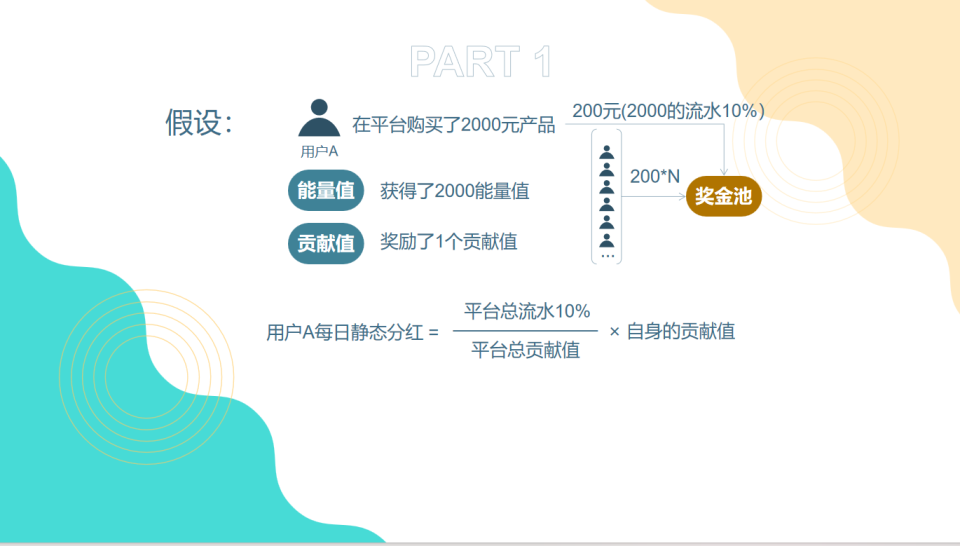
一些商家之所以能在此模式下取得巨大的成功，除了产品质量的保证外，合理的商业模式也起到了至关重要的作用。只有结合优质的产品与创新的商业模式，才能在竞争激烈的电商市场中脱颖而出。

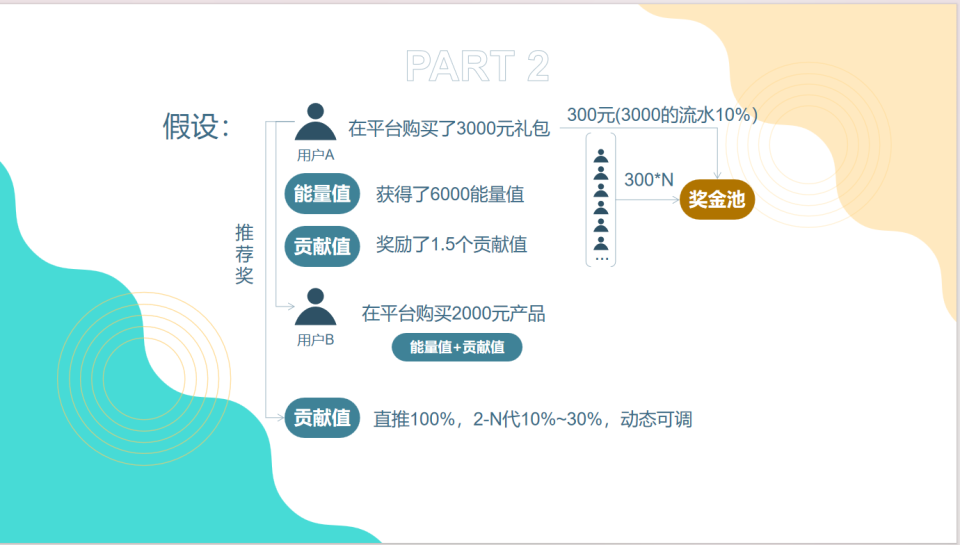
综上所述，循环购模式是一种创新的消费返利模式，它既能满足消费者的购物需求，又能为他们带来额外的收益。作为消费者，我们也应该保持警惕，选择那些信誉良好的平台和商家进行消费，以确保我们的权益得到保障。

需要咨询模式或者是软件开发的企业家，可以后台私信小编或在评论区留下您的联系方式

注明：小编所有分析的项目，只是分析商业模式

了解更多互联网资讯。需要开发 DAPP，小程序,app，分销模式，商城系统软件等关注小编