文章目录
- 基本思想
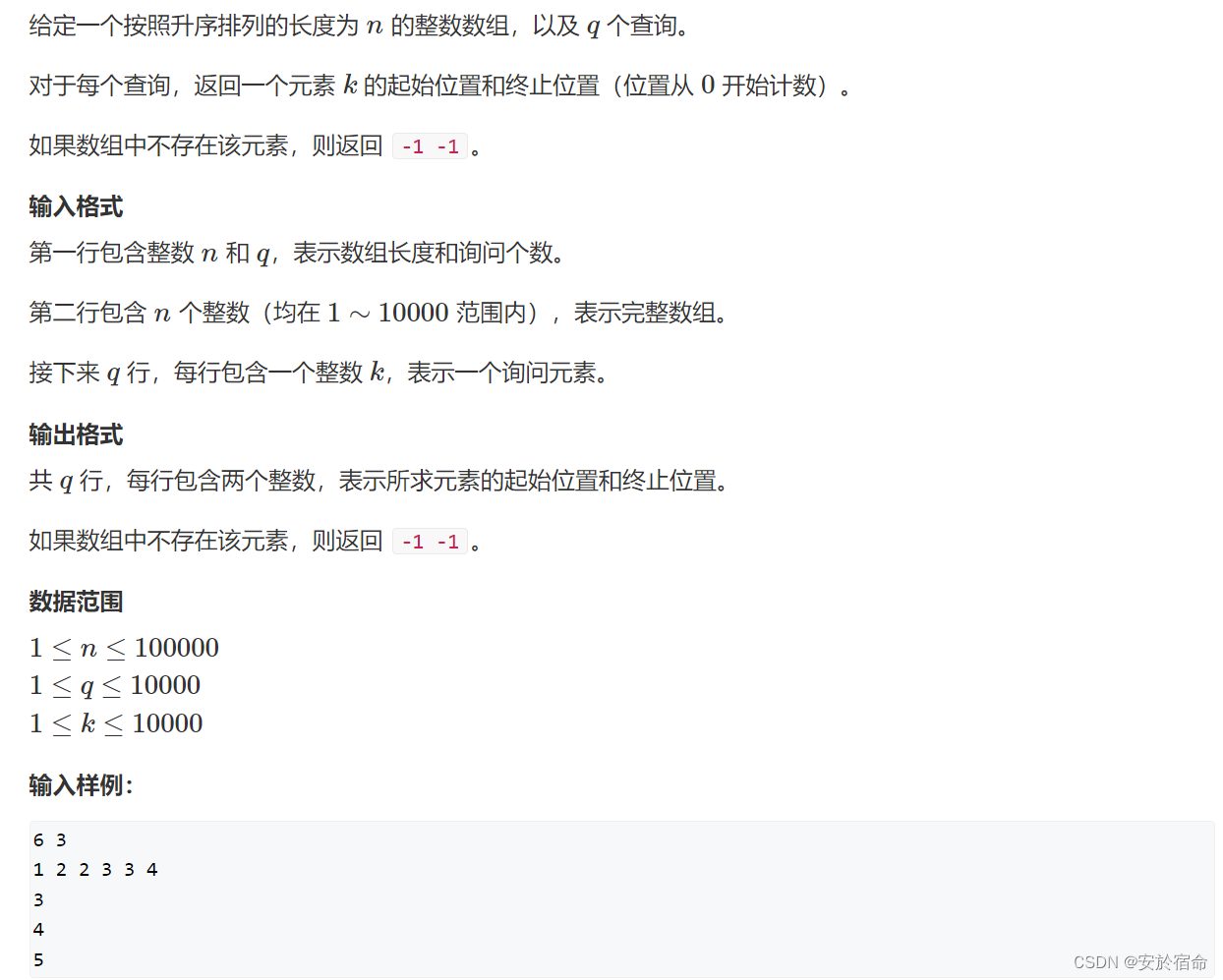
- 1.数的范围
- 2.搜索旋转排序数组
- 3.搜索插入位置
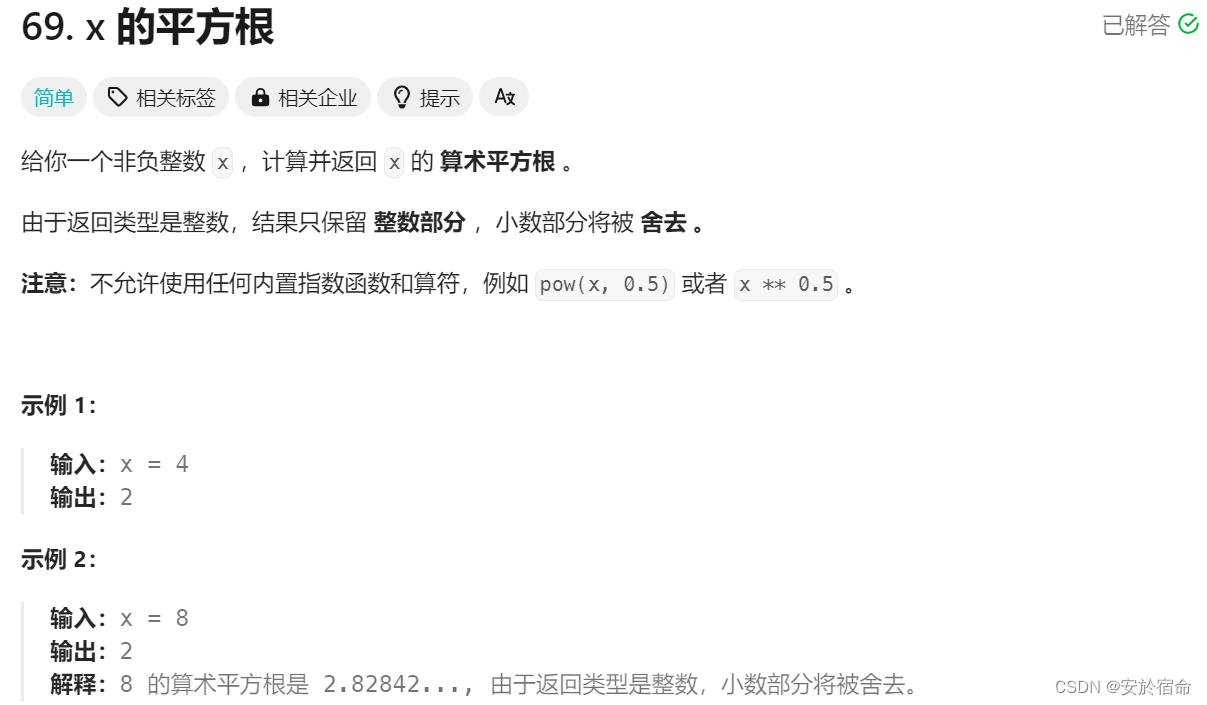
- 4.x的平方根
- 总结

基本思想
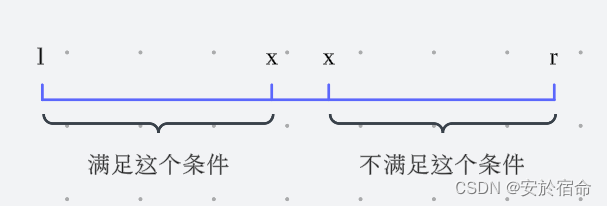
二分查找的必要条件并不是单调,而是当我给定一个边界条件,然后左边满足这个边界条件,右边不满足这个边界条件,然后可以查找这个临界点,这就是二分查找
接下来我们具体讨论该怎么做
我们先讨论满足这个条件的一边,首先我们取mid=(l+r)/2,如果这个mid<x证明mid在x的左边,mid可能是边界所以要包含mid,所以将范围更新为[mid,r],如果mid>x,证明mid在x的右边,由于右边是不满足条件的,所以直接把mid舍去,更新范围为[l,mid-1],以此类推最后当l==r的时候,就是边界x
第二种:我们来讨论一下不满足条件的一边,如果我们需要找到右边界x,那么首先定义一个mid=(l+r+1)/2,如果mid<x证明不满足右边条件的在右边,所以要将mid舍去,将范围更新为[mid+1,r],如果mid>x证明mid在x的右边,所以满足右边的条件,由于右边都可能存在满足条件的,所以不能舍弃边界mid,所以将边界更新为[l,mid].
大致就分为上面两种情况,注意:如果是第二种情况的时候,需要+1,因为如果不向上取整的话,会造成死循环,如果不向上取整的话,当l=r-1的时候,意思就是当l和r相差1的时候,mid始终等于l这样就产生了死循环,但是如果向上取整的话,最后mid就等于r,就会跳出循环
接下来我们了解了基本算法来练习两道题:
1.数的范围
根据题目描述可以知道,这道题可以用二分查找
#include<iostream>
using namespace std;
//数组大小和需要的变量
const int N=100000;
int a[N];
int q,n;
int main()
{
//输入变量
cin>>n>>q;
//初始化数组
for(int i=0;i<n;i++)cin>>a[i];
//q行数据
while(q>0)
{
//输入需要查找的数据
int x;
cin>>x;
//先定义左右边界
int l=0,r=n-1;
while(l<r)
{
//二分
int mid=(l+r)/2;
//边界条件
if(a[mid]>=x)r=mid;
else l = mid+1;
}
//出循环判断l对应的值是否和x相等,如果相等则继续,如果不相等则直接打印-1 -1
if(a[l]!=x)cout<<"-1 -1"<<endl;
else
{
//先输出上个循环的l
cout<<l<<' ';
//确定边界
int l=0,r=n-1;
//对右边界的条件进行二分
while(l<r)
{
int mid=(l+r+1)/2;//向上取整,防止死循环
if(a[mid]<=x)l=mid;
else r=mid-1;
}
//输出有边界
cout<<l<<endl;
}
q--;
}
return 0;
}
2.搜索旋转排序数组
思路:首先这道题要求时间复杂度是O(logn),那么首先想到的就是二分,虽然这道题给的不是一个完整的有序的数组,但是是局部有序的 ,我们二分之后总是能保证左区间或者右区间是有序的,所以我们只需要判断一个有序区间是否存在这个数,如果不存在说明在另一个区间,直接else进入另一个区间,所以第一个大的if else是讨论左区间和右区间的有序性,第二个if else是讨论是在左区间或者右区间,去对这个数组的范围进行更新,范围条件,如果mid对应的值和target相等直接返回下标mid,如果最后不相等,直接跳出循环返回-1
代码展示
int search(int* nums, int numsSize, int target) {
if(numsSize==1)
{
return nums[0]==target?0:-1;
}
int l=0;
int r=numsSize-1;
while(l<=r)
{
int mid=(l+r)/2;
if(nums[mid]==target)
{
return mid;
}
if(nums[mid]>=nums[l])
{
if(nums[mid]>target&&nums[l]<=target)
{
r=mid-1;
}
else
{
l=mid+1;
}
}
else{
if(nums[mid]<target&&target<=nums[r])
{
l=mid+1;
}
else
{
r=mid-1;
}
}
}
return -1;
}
3.搜索插入位置
这道题也是一个简单的二分,注意边界条件即可
int searchInsert(int* nums, int numsSize, int target) {
if(target>nums[numsSize-1])
{
return numsSize;
}
int l=0,r=numsSize-1;
while(l<r)
{
int mid=(l+r)/2;
if(nums[mid]>=target)r=mid;
else l=mid+1;
}
return l;
}
4.x的平方根
这道题是一道简单的二分
首先定义左边界和右边界,然后定义一个范围值ans,然后进行二分如果中间值的平方<=x说明答案在右边,将ans更新,然后更新区间范围,如果两个数的乘积大于x的话说明在在区间的左边,所以更新r,由于我们需要的是向下取整,所以在更新l的时候,就直接更新ans,如果在r变化的时候更新ans会使最后的ans变大
int mySqrt(int x) {
int l=0;
int r=x;
int ans=-1;
while(l<=r)
{
int mid=(l+r)/2;
if((long long)mid*mid<=x)
{
ans=mid;
l=mid+1;
}
else
{
r=mid-1;
}
}
return ans;
}
总结
当你理解了二分查找的原理,并且掌握了它的实现方法,你就掌握了一种高效查找数据的技巧。二分查找是一种简单而又强大的算法,在处理大规模数据时能够显著提高搜索效率。通过不断地练习和应用,你可以在编程的世界里更加游刃有余地运用这一技巧。希望本文对你有所启发,能够帮助你更深入地理解二分查找算法,并在实际应用中发挥其作用。在编程的道路上,不断学习,不断进步,愿你能够越走越远,探索更多的算法与数据结构的奥秘。