代码随想录阅读笔记-回溯【全排列 II】

news2024/11/20 20:38:29

题目

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

  • 输入：nums = [1,1,2]
  • 输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

  • 输入：nums = [1,2,3]
  • 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

思路 

本题和上一道题的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

这里又涉及到去重了。

在组合总和以及子集问题中我们分别详细讲解了组合问题和子集问题如何去重。

那么排列问题其实也是一样的套路。

还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

我以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

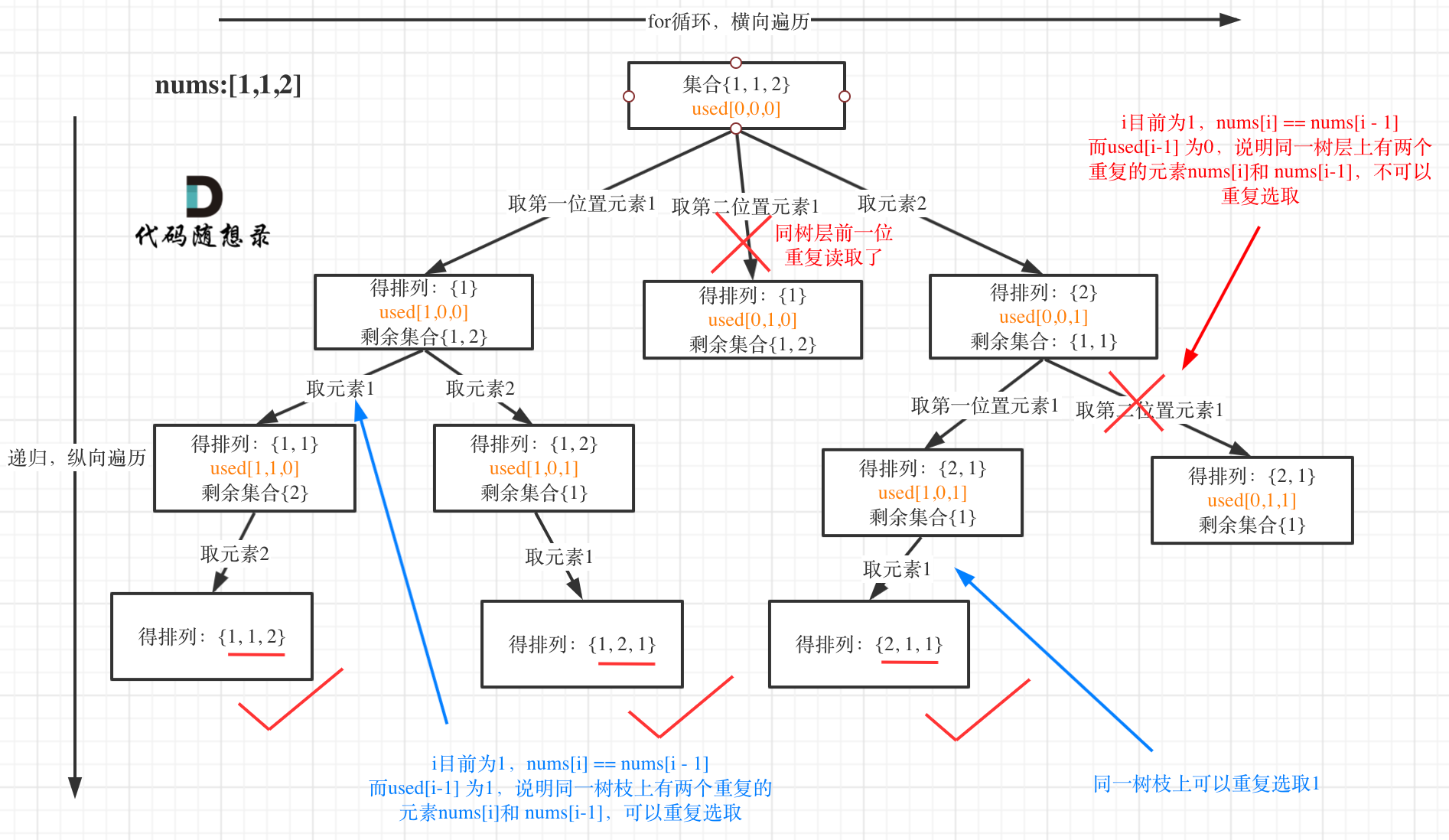
47.全排列II1

图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

代码如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            if (used[i] == false) {
                used[i] = true;
                path.push_back(nums[i]);
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // 排序
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案，我们需要 O(n) 去复制最终放到 result 数组
// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素
  • 时间复杂度: O(n! * n)
  • 空间复杂度: O(n)

拓展

大家发现，去重最为关键的代码为：

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

如果改成 used[i - 1] == true， 也是正确的!，去重代码如下：

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

这么说是不是有点抽象？

来来来，我就用输入: [1,1,1] 来举一个例子。

树层上去重(used[i - 1] == false)，的树形结构如下：

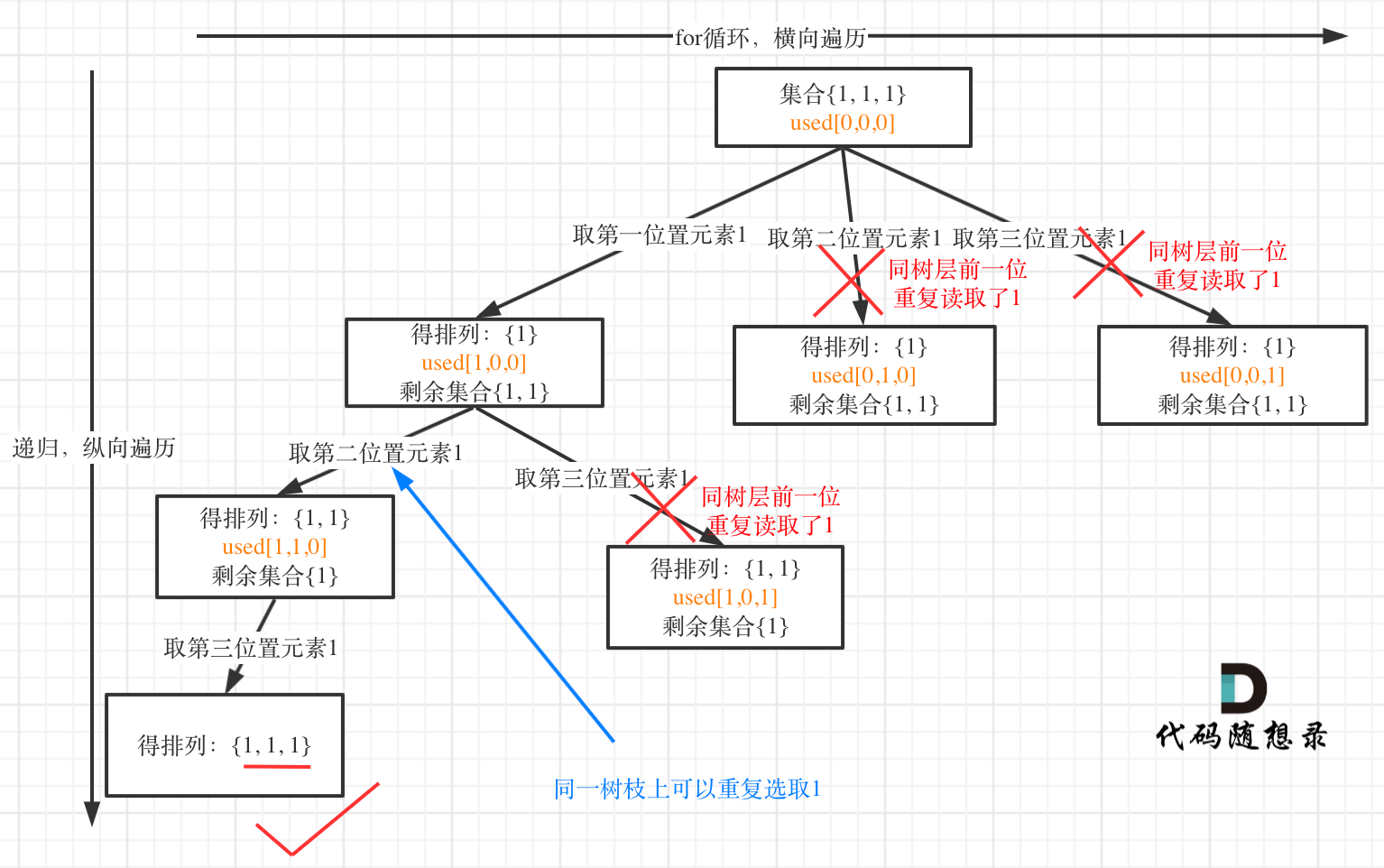
47.全排列II2

树枝上去重（used[i - 1] == true）的树型结构如下：

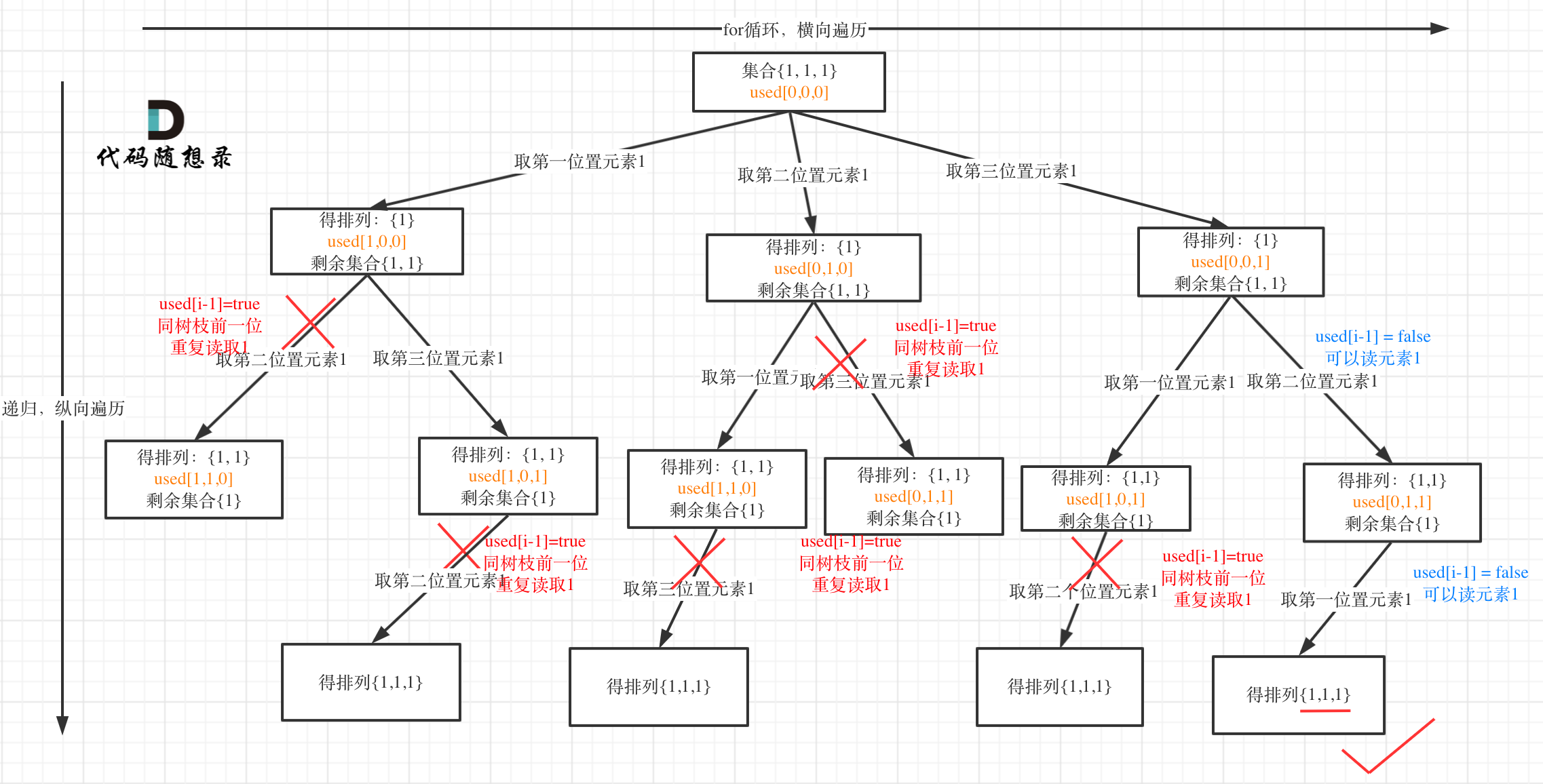
47.全排列II3

大家应该很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。

接下来着重 复习并总结一下回溯法中需要去重的问题

在子集Ⅱ中的去重和 递增子序列中的去重 都是 同一父节点下本层的去重。

子集Ⅱ问题也可以使用set针对同一父节点本层去重，但子集问题一定要排序，为什么呢？

我用没有排序的集合{2,1,2,2}来举例子画一个图，如图：

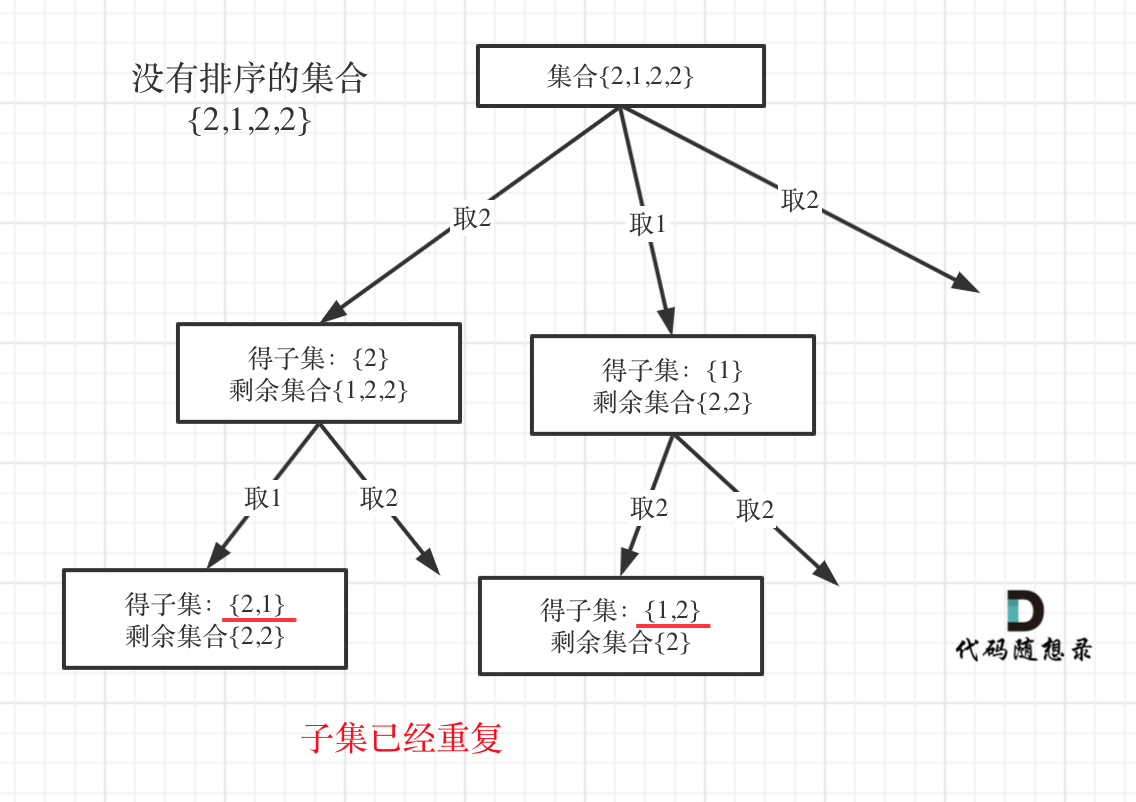
90.子集II2

图中，大家就很明显的看到，子集重复了。那么下面我针对子集Ⅱ问题给出使用set来对本层去重的代码实现。

​​​​​​​子集Ⅱ问题

使用set去重的版本如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);
        unordered_set<int> uset; // 定义set对同一节点下的本层去重
        for (int i = startIndex; i < nums.size(); i++) {
            if (uset.find(nums[i]) != uset.end()) { // 如果发现出现过就pass
                continue;
            }
            uset.insert(nums[i]); // set跟新元素
            path.push_back(nums[i]);
            backtracking(nums, i + 1, used);
            path.pop_back();
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }
};

再补充一些常见的错误写法，

错误写法一

把uset定义放到类成员位置，然后模拟回溯的样子 insert一次，erase一次。

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    unordered_set<int> uset; // 把uset定义放到类成员位置
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);

        for (int i = startIndex; i < nums.size(); i++) {
            if (uset.find(nums[i]) != uset.end()) {
                continue;
            }
            uset.insert(nums[i]);   // 递归之前insert
            path.push_back(nums[i]);
            backtracking(nums, i + 1, used);
            path.pop_back();
            uset.erase(nums[i]);    // 回溯再erase
        }
    }

在树形结构中，如果把unordered_set uset放在类成员的位置（相当于全局变量），就把树枝的情况都记录了，不是单纯的控制某一节点下的同一层了。

如图：

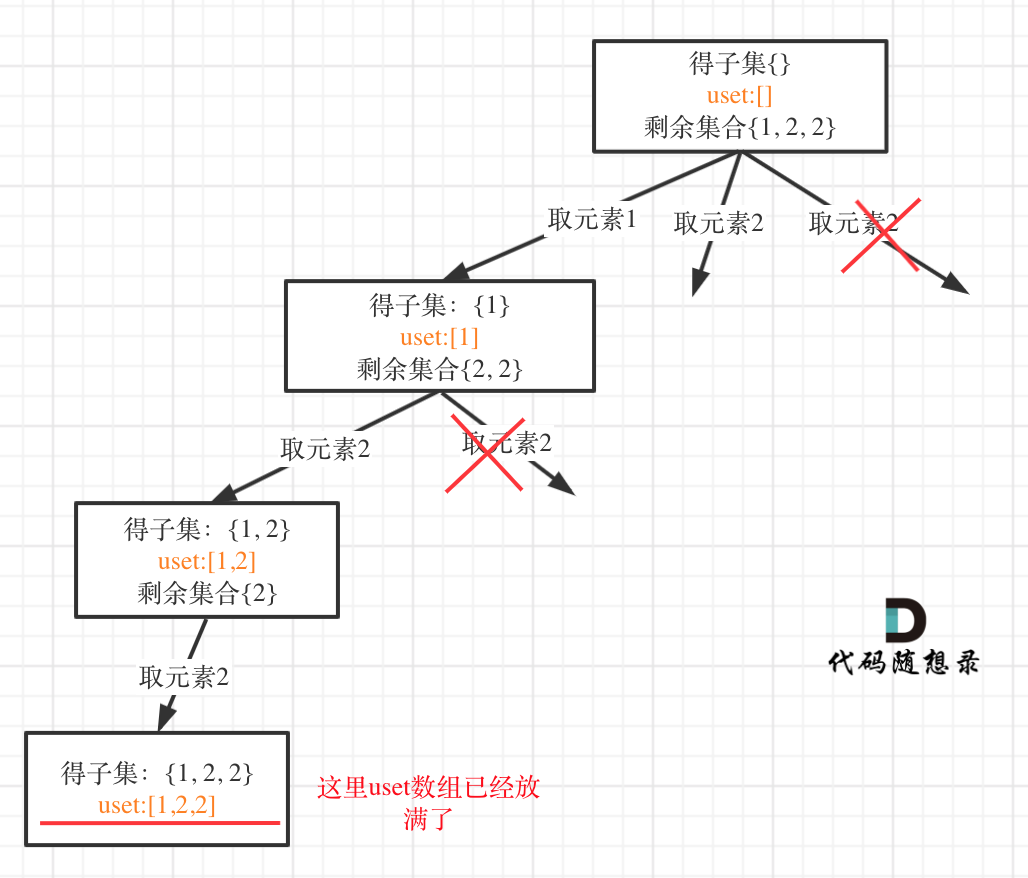
90.子集II1

可以看出一旦把unordered_set uset放在类成员位置，它控制的就是整棵树，包括树枝。

所以这么写不行！

错误写法二

有同学把 unordered_set uset; 放到类成员位置，然后每次进入单层的时候用uset.clear()。

代码如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    unordered_set<int> uset; // 把uset定义放到类成员位置
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);
        uset.clear(); // 到每一层的时候，清空uset
        for (int i = startIndex; i < nums.size(); i++) {
            if (uset.find(nums[i]) != uset.end()) {
                continue;
            }
            uset.insert(nums[i]); // set记录元素
            path.push_back(nums[i]);
            backtracking(nums, i + 1, used);
            path.pop_back();
        }
    }

uset已经是全局变量，本层的uset记录了一个元素，然后进入下一层之后这个uset（和上一层是同一个uset）就被清空了，也就是说，层与层之间的uset是同一个，那么就会相互影响。

所以这么写依然不行！

组合问题和排列问题，其实也可以使用set来对同一节点下本层去重，下面我都分别给出实现代码。

组合总和 II

使用set去重的版本如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            if (uset.find(candidates[i]) != uset.end()) {
                continue;
            }
            uset.insert(candidates[i]); // 记录元素
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i + 1);
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        path.clear();
        result.clear();
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

全排列 II

使用set去重的版本如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
        for (int i = 0; i < nums.size(); i++) {
            if (uset.find(nums[i]) != uset.end()) {
                continue;
            }
            if (used[i] == false) {
                uset.insert(nums[i]); // 记录元素
                used[i] = true;
                path.push_back(nums[i]);
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // 排序
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

两种写法的性能分析

需要注意的是：使用set去重的版本相对于used数组的版本效率都要低很多，大家在leetcode上提交，能明显发现。

主要是因为程序运行的时候对unordered_set 频繁的insert，unordered_set需要做哈希映射（也就是把key通过hash function映射为唯一的哈希值）相对费时间，而且insert的时候其底层的符号表也要做相应的扩充，也是费时的。而使用used数组在时间复杂度上几乎没有额外负担！

使用set去重，不仅时间复杂度高了，空间复杂度也高了，组合，子集，排列问题的空间复杂度都是O(n)，但如果使用set去重，空间复杂度就变成了O(n^2)，因为每一层递归都有一个set集合，系统栈空间是n，每一个空间都有set集合。而used数组是全局变量，每层与每层之间公用一个used数组，所以空间复杂度是O(n + n)，最终空间复杂度还是O(n)。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1609638.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

七牛云配置，图片上传、查看的使用（备忘）

七牛云配置，图片上传、查看的使用（备忘）

修改配置文档 修改新创建的空间的地区名 访问设置为 公开&#xff0c;不然会有访问时间限制 检查 上传和查看的链接是否正确。
阅读更多...
centos linux 7.9安装php8.2.18不支持mysqli模块，如何解决？

centos linux 7.9安装php8.2.18不支持mysqli模块，如何解决？

&#x1f3c6;本文收录于「Bug调优」专栏&#xff0c;主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案&#xff0c;希望能够助你一臂之力&#xff0c;帮你早日登顶实现财富自由&#x1f680;&#xff1b;同时&#xff0c;欢迎大家关注&&收藏&&…
阅读更多...
钉钉对接T+生成总账凭证

钉钉对接T+生成总账凭证

客户介绍&#xff1a; 某餐饮连锁企业是一个专注于特色风味徽州菜的餐饮品牌&#xff0c;总部位于杭州市&#xff0c;其推出的各式特色徽菜深受市场的好评&#xff0c;在杭州本地的餐饮市场中有着很强的竞争力。公司ERP使用用友T系统&#xff0c;通过钉钉管理员工费用报销流程…
阅读更多...
【精简改造版】大型多人在线游戏BrowserQuest服务器Golang框架解析（1）——功能清单

【精简改造版】大型多人在线游戏BrowserQuest服务器Golang框架解析（1）——功能清单

1.匿名登录 2.服务连接 3.新手引导 4.随机出生点 5.界面布局 6.玩法帮助 7.NPC会话 8.成就系统 9.成就达成 10.用户聊天 11.战斗&信息展示 12.药水使用 13.副本传送 14.玩家死亡 15.超时断开
阅读更多...
【大语言模型+Lora微调】10条对话微调Qwen-7B-Chat并进行推理 (聊天助手)

【大语言模型+Lora微调】10条对话微调Qwen-7B-Chat并进行推理 (聊天助手)

代码&#xff1a;https://github.com/QwenLM/Qwen/tree/main 国内源安装说明&#xff1a;https://modelscope.cn/models/qwen/Qwen-7B-Chat/summary 通义千问&#xff1a;https://tongyi.aliyun.com/qianwen 一、环境搭建 下载源码 git clone https://github.com/QwenLM/Qwen…
阅读更多...
浏览器渲染流程中的 9 个面试点

浏览器渲染流程中的 9 个面试点

记得 08 年以前&#xff0c;打开网页的时候一个页面卡死整个浏览器凉凉。 这是因为当时浏览器是单进程架构&#xff0c;一个页面或者插件卡死&#xff0c;整个浏览器都会崩溃&#xff0c;非常影响用户体验。 经过了一代代工程师的设计&#xff0c;现代浏览器改成了多进程架构&…
阅读更多...
C++：继承作业题

C++：继承作业题

1. 关于以下菱形继承说法不正确的是&#xff08; &#xff09; &#xfeff;class B {public: int b;};class C1: public B {public: int c1;};class C2: public B {public: int c2;};class D : public C1, public C2 {public: int d;};A.D总共占了20个字节B.B中的内容总共在D…
阅读更多...
2024物理学、电子电路与通信工程国际学术会议(ICPECCE2024)

2024物理学、电子电路与通信工程国际学术会议(ICPECCE2024)

2024物理学、电子电路与通信工程国际学术会议(ICPECCE2024) 会议简介 2024国际物理、电子电路与通信工程学术会议&#xff08;ICPECCE2024&#xff09;将在深圳隆重举行。本次会议旨在汇聚全球物理、电子电路、通信工程等领域的专家学者&#xff0c;共同探讨最新研究成果和…
阅读更多...
《从零开始的Java世界》05异常处理

《从零开始的Java世界》05异常处理

《从零开始的Java世界》系列主要讲解Javase部分&#xff0c;从最简单的程序设计到面向对象编程&#xff0c;再到异常处理、常用API的使用&#xff0c;最后到注解、反射&#xff0c;涵盖Java基础所需的所有知识点。学习者应该从学会如何使用&#xff0c;到知道其实现原理全方位式…
阅读更多...
洛谷 P1131 [ZJOI2007] 时态同步

洛谷 P1131 [ZJOI2007] 时态同步

思路&#xff1a;树形DP 这道题总的来说有点贪心的味道&#xff0c;贪心在我们需要把这个时间点加到哪一条边上。 借用一下一位洛谷大佬的图&#xff1a; 其实这样看出来&#xff0c;如果说越靠近根的那条边加长&#xff0c;其实价值最小&#xff0c;所以我们需要尽量向靠近根…
阅读更多...
AbstractQueuedSynchronizer 源码解析

AbstractQueuedSynchronizer 源码解析

AbstractQueuedSynchronizer 源码解析 文章目录 AbstractQueuedSynchronizer 源码解析一、CAS二、字段分析三、内部类 Node1、CLH 队列2、源码分析 四、内部类 ConditionObject1、字段分析2、方法分析1、await2、signal 五、方法分析1、独占式下的 AQS1、acquire 独占式获取资源…
阅读更多...
14.基础乐理-音级、基本音级、变化音级

14.基础乐理-音级、基本音级、变化音级

音级&#xff1a; 乐音体系中的每一个音&#xff0c;都叫 音级。 基本音级&#xff1a; 基本音级是 CDEFGAB 它们七个&#xff0c;在钢琴上使用白键展示的&#xff0c;没有任何升降号、没有任何重升重降号的。 变化音级&#xff1a; 除了 CDEFGAB 这七个音&#xff0c;都叫变化…
阅读更多...
面向对象练习坦克大兵游戏

面向对象练习坦克大兵游戏

游戏玩家&#xff08;名称&#xff0c;生命值&#xff0c;等级&#xff09;&#xff0c;坦克&#xff0c;大兵类&#xff0c;玩家之间可以相互攻击&#xff0c;大兵拥有武器&#xff0c;用枪弹和反坦克炮弹&#xff0c;造成攻击不同&#xff0c;坦克攻击值固定&#xff0c;请设…
阅读更多...
logisim 图解超前进位加法器原理解释

logisim 图解超前进位加法器原理解释

鄙人是视频作者&#xff0c;文件在视频简介的网盘链接。 找规律图解超前进位加法器与原理解释_哔哩哔哩_bilibili 一句话就是“把能导致进位到这个位置的情况全都穷举一遍。” 穷举情况看图中算式。 视频讲解比较啰嗦。
阅读更多...
JavaFX--基础简介(1)

JavaFX--基础简介(1)

一、介绍 中文官网&#xff1a;JavaFX中文官方网站OpenJFX 是一个开源项目,用于桌面、移动端和嵌入式系统的下一代客户端应用程序平台。openjfx.cn是OpenJFX(JavaFX)的标准中文翻译网站&#xff0c;致力于方便开发者阅读官方文档和教程。https://openjfx.cn/ JavaFX 是一个开…
阅读更多...
【一文配置好Python开发环境】Python创建虚拟环境，一键更换国内镜像源

【一文配置好Python开发环境】Python创建虚拟环境，一键更换国内镜像源

一、使用Python自带的venv创建虚拟环境 首先&#xff0c;确保你的Python安装中包含了venv模块。你可以在命令行中运行以下命令来检查&#xff1a; python -m venv --help进入代码目录&#xff0c;创建一个新的虚拟环境。在命令行中运行以下命令&#xff1a; python -m venv …
阅读更多...
Llama 3王者归来，可与GPT-4分庭抗礼，开源模型即将追上闭源模型了？

Llama 3王者归来，可与GPT-4分庭抗礼，开源模型即将追上闭源模型了？

“有史以来最强大的开源大模型”Llama 3引爆AI圈&#xff0c;马斯克点赞&#xff0c;英伟达高级科学家Jim Fan直言&#xff0c;Llama 3将成为AI大模型发展历程的“分水岭”&#xff0c;AI顶尖专家吴恩达称Llama3是他收到的最好的礼物。 4月18日&#xff0c;AI圈再迎重磅消息&a…
阅读更多...
ubuntu22.04下编译ffmpeg和ffplay

ubuntu22.04下编译ffmpeg和ffplay

Ubuntu22.04 下编译安装 ffmpeg 和 ffplay 一、下载源码包 1.1 官方下载链接&#xff1a;Download FFmpeg 可以手动下载&#xff0c;也可以命令行下载&#xff1a; wget http://www.ffmpeg.org/releases/ffmpeg-7.0.tar.xz 1.2 下载完解压 tar -xvf ffmpeg-7.0.tar.xz…
阅读更多...
X-314智能合约：金融创新的强大引擎

X-314智能合约：金融创新的强大引擎

&#x1f4a5;火爆到烫手的X-314智能合约&#x1f525; X-314智能合约是基于以太坊区块链开发的&#xff0c;具有高度可定制性和灵活性。 ave开单独板块&#xff1b;详细资料已经准备好&#xff1b;对web3感兴趣的大佬货&#xff1b;多交流多指导&#x1f91d; ​X-314智能合…
阅读更多...
新质生产力如何点燃乡村振兴之火？（2010-2022年）

新质生产力如何点燃乡村振兴之火？（2010-2022年）

数据来源&#xff1a;主要来源于《中国国统计年鉴》、《中国能源统计年鉴》、《中国农村统计年鉴》、《中国人口和就业统计年鉴》、《中国城乡建设统计年鉴》以及各省份统计年鉴。时间范围&#xff1a;2010-2022年数据范围&#xff1a;各省、市、自治区数据指标&#xff1a; 本…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023