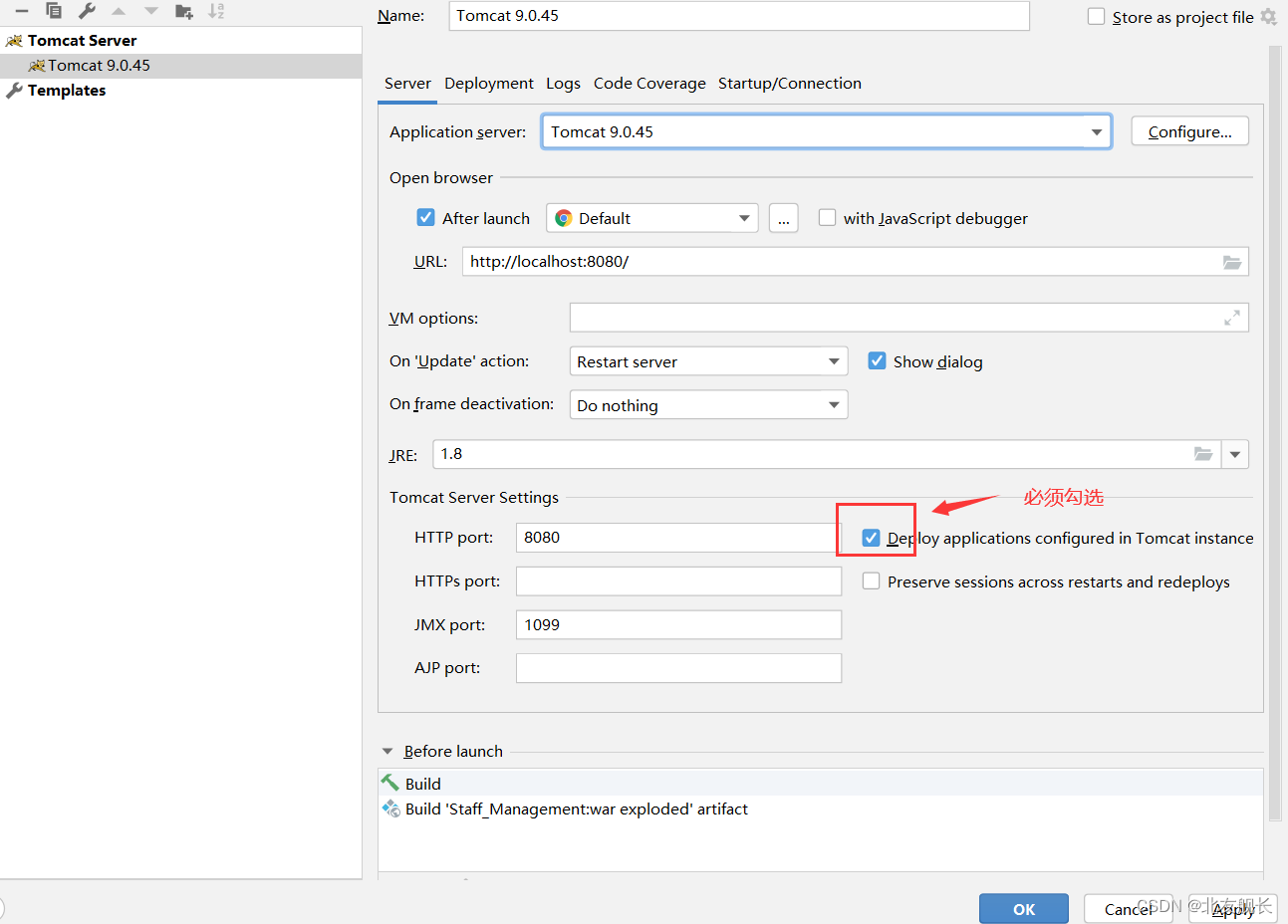
思路：树形DP

这道题总的来说有点贪心的味道，贪心在我们需要把这个时间点加到哪一条边上。

借用一下一位洛谷大佬的图：

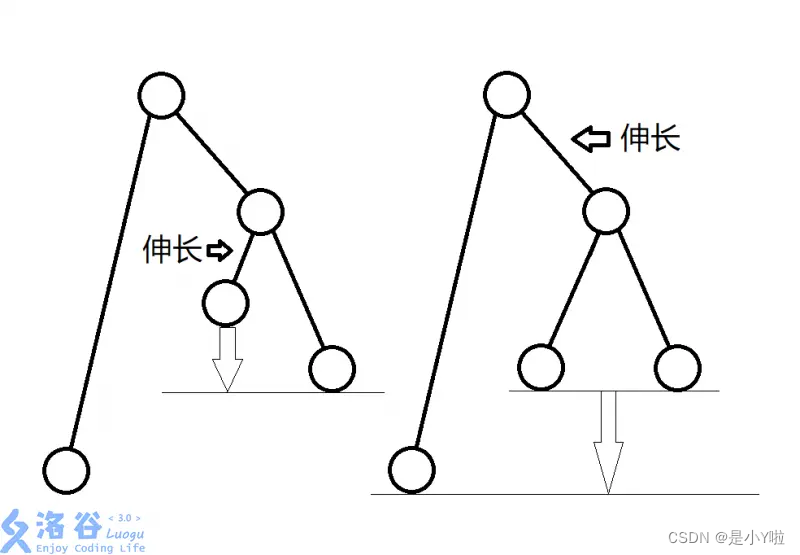
其实这样看出来，如果说越靠近根的那条边加长，其实价值最小，所以我们需要尽量向靠近根的地方加时间点。

这样的话，我们可以首先求出来距离根结点最深的那个叶节点，用dp数组当作更新距离的数组，

我们直接dp[i] =max(dp[i],dp[son]+w[son])其实也就是这个样子。这个时候我们就找到了距离根节点的最长距离。

然后，我们就从根节点开始，对于每一条边进行更新，也就是dp[u]-(dp[son]+w[son])这样就可以了。作者写的w数组是二维的，因为如果设置一维的话并不知道是哪一个结点有权值。大家可以仿照别的题解写一下图的存储，这里只是提供一种思路和稍微简单的暴力思路。

注意：由于我们已经求出来每一个结点距离最下面的叶结点的最长距离了，所以我们没必要一次次判断最大值，直接在最后累加就行了。所以才会有counts+=....而不是一步一步再去判断最小价值。

上代码：

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<cmath> 
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<deque>
#include <iomanip>
#include<sstream>
#include<numeric>
#include<map>
#include<limits.h>
#include<unordered_map>
#include<set>
#define int long long
#define MAX 9999
#define inf 0x3f3f3f3f
#define _for(i,a,b) for(int i=a;i<(b);i++)
using namespace std;
typedef pair<int, int> PII;
int n, m;
int counts;
int dx[] = { 0,1,0,-1};
int dy[] = { 1,0,-1,0 };
vector<int>vec[MAX];
int dp[MAX];
int w[MAX][MAX];
int top[MAX];
void dfs(int u,int fa) {
    for (int i = 0; i < vec[u].size(); i++) {
        int son = vec[u][i];
        if (son == fa)continue;
        dfs(son, u);
        dp[u] = max(dp[u], dp[son] + w[u][son]);
    }
    for (int i = 0; i < vec[u].size(); i++) {
        int son = vec[u][i];
        if (son == fa)continue;
        counts += dp[u] - (dp[son] + w[u][son]);
    }
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);
    cin >> n;
    cin >> m;
    for (int i = 0; i < n-1; i++) {
        int a, b, t;
        cin >> a >> b >> t;
        vec[a].push_back(b);
        vec[b].push_back(a);
        w[a][b] = t;
        w[b][a] = t;
    }
    dfs(m, 0);
    cout << counts;
    return 0;
}