比较C++在for循环中的i++和++i以及i++的O2优化的效率:++i真的比i++快吗
前言
对i++和++i的争论褒贬不一,不知从何时起(大概是学C的时候老师就是这么教的)我的习惯是在for循环中使用i++而不是++i
for (int i = 0; i < n; i++) // 典
但是看到一些博客说++i比i++的效率高。
虽然现在的编译器的优化、机器的性能提升之类导致i++和++i的区别应该不会很大,但我还是决定做一个实验进行一下对比。
实验环境
- 操作系统:deepin 5.3.15-6apricot
- g++版本:gcc version 8.3.0 (Uos 8.3.0.3-3+rebuild)
- screen版本:Screen version 4.06.02 (GNU) 23-Oct-17
实验步骤
首先编写了两个简单的cpp文件,分别命名为i++.cpp和++i.cpp
其中i++.cpp为:
#include <iostream>
#include <time.h>
using namespace std;
#define forTo 10000000000000
#define perCout 1000000000
int main() {
clock_t start = clock();
for (long long i = 0; i < forTo; i++) {
if (i % perCout == 0) {
cout << i << "(" << 100. * i / forTo << "%)" << endl;
}
}
puts("End..");
cout << "Time consume: " << double(clock() - start) / CLOCKS_PER_SEC << endl;
return 0;
}
++i.cpp为:
#include <iostream>
#include <time.h>
using namespace std;
#define forTo 10000000000000
#define perCout 1000000000
int main() {
clock_t start = clock();
for (long long i = 0; i < forTo; ++i) {
if (i % perCout == 0) {
cout << i << "(" << 100. * i / forTo << "%)" << endl;
}
}
puts("End..");
cout << "Time consume: " << double(clock() - start) / CLOCKS_PER_SEC << endl;
return 0;
}
上述两个文件的主要部分都是一个循环,一共循环10000000000000次,每循环1000000000次打印一次
二者唯一的区别是第10行
+ for (long long i = 0; i < forTo; i++) {
- for (long long i = 0; i < forTo; ++i) {
接着开启三个screen终端,在每个终端中分别编译源文件。三个终端的名称分别为i++、++i和i++O2
- 在终端i++中,使用指令
g++ -O0 i++.cpp -o i++进行编译 - 在终端++i中,使用指令
g++ -O0 ++i.cpp -o ++i进行编译 - 在终端i++O2中,使用指令
g++ -O2 i++.cpp -o i++O2进行编译
前两个终端不使用O2优化,第三个终端使用O2优化
为了使实验尽可能地在相同的条件下运行,提前在三个终端中输入好运行指令:./i++、./++i、./i++O2
接着以尽快的速度(1秒内)在三个终端中分别键入回车,让三个程序在尽可能短的时间内“同时”启动运行并等待结果。

经过一段时间后(约7h),我们得到了运行结果:
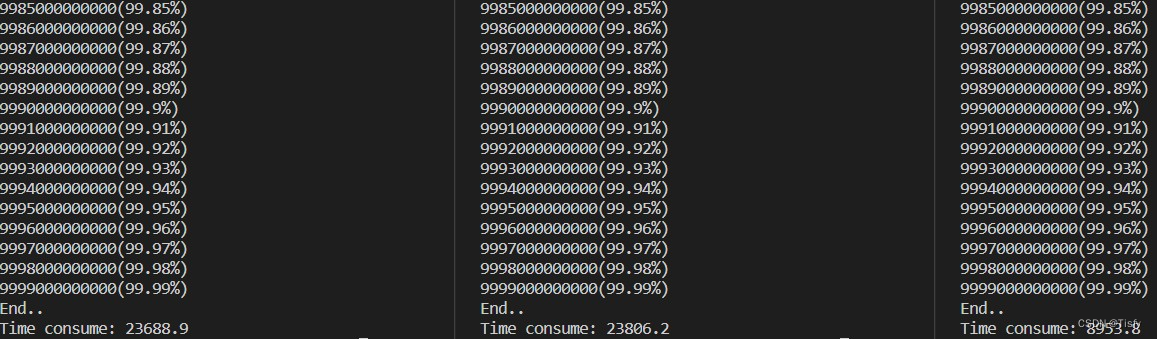
结果显示:
- 在for循环中使用i++计算10000000000000次,每1000000000次打印一次,所消耗的时间为23688.9秒
- 在for循环中使用++i计算10000000000000次,每1000000000次打印一次,所消耗的时间为23806.2秒
- 在for循环中使用i++计算10000000000000次,每1000000000次打印一次,并开启O2优化,所消耗的时间为8953.8秒
这表明:
- i++并且开O2优化的执行时间“远”小于i++或++i不开优化的执行时间
- 不开启O2优化的情况下,i++和++i的效率相差不大,使用++i的耗时略长,使用i++的时间消耗约为++i的99.507%
进一步实验:
在上述实验中,虽说每隔1000000000次打印一次,但在循环中仍打印了10000次。这1万次的打印会消耗不少的时间,并且也可以引起一定的误差。
因此,在实验二中,我们取消了循环中的打印,只保留循环结束后的时间打印。
同样新建了两个简单的cpp文件:i++NC.cpp和++iNC.cpp。其中NC的意思是:Not Cout
i++NC.cpp为:
#include <iostream>
#include <time.h>
using namespace std;
#define forTo 10000000000000
#define perCout 1000000000
int main() {
clock_t start = clock();
for (long long i = 0; i < forTo; i++) {
;
}
puts("End..");
cout << "Time consume: " << double(clock() - start) / CLOCKS_PER_SEC << endl;
return 0;
}
++iNC.cpp为
#include <iostream>
#include <time.h>
using namespace std;
#define forTo 10000000000000
#define perCout 1000000000
int main() {
clock_t start = clock();
for (long long i = 0; i < forTo; ++i) {
;
}
puts("End..");
cout << "Time consume: " << double(clock() - start) / CLOCKS_PER_SEC << endl;
return 0;
}
二者的唯一区别仍为第10行
接着使用类似实验一的方式在三个终端中对文件进行编译、执行
编译命令分别为:
g++ -O0 i++.cpp -o i++g++ -O0 ++i.cpp -o ++ig++ -O2 i++.cpp -o i++O2
执行程序的命令分别为:
./i++NC./++iNC./i++NCO2

接近同时(1秒内)启动三个程序,并观察运行结果

可以看到:
- 在for循环中使用i++计算10000000000000次,所消耗的时间为16987秒
- 在for循环中使用++i计算10000000000000次,所消耗的时间为16994.3秒
- 在for循环中使用i++计算10000000000000次,并开启O2优化,所消耗的时间为2.2e-05秒
这表明:
- i++并且开O2优化的执行时间远小于i++或++i不开优化的执行时间
- 不开启O2优化的情况下,i++和++i的效率相差不大,使用++i的耗时略长,使用i++的时间消耗约为++i的99.957%
Conclusion
- O2优化很多时候确实能够大大提高代码的执行效率
- (在for循环中使用)i++和++i的区别真的不大,按照自己喜欢的使用就好
End
附 本实验所有文件的MD5值:(使用命令:md5sum 文件名计算得到)
| 文件 | MD5值 |
|---|---|
| ++i | a0a4916914604260d15f915b69bd6680 |
| ++i.cpp | 87f7bce79f6da8aab379d50855623b49 |
| ++iNC | 8f3824486c3eda26ee7c687b48fddf17 |
| ++iNC.cpp | c83f8a7252ab83b7c1aacc1371464711 |
| i++ | d706151497301d37c17f2766231493c1 |
| i++.cpp | ce237f15c3b2376f064c036985389d40 |
| i++NC | f92ba414cd60df7d44a62bca23378d61 |
| i++NC.cpp | 163bc47ce3176b73306568ef542eb3a0 |
| i++NCO2 | 7f2e8e8998361aab19e4c1decf29026a |
| i++O2 | 4f8cbacc480c8dbf5a62e433535bc9b1 |
原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/128675905