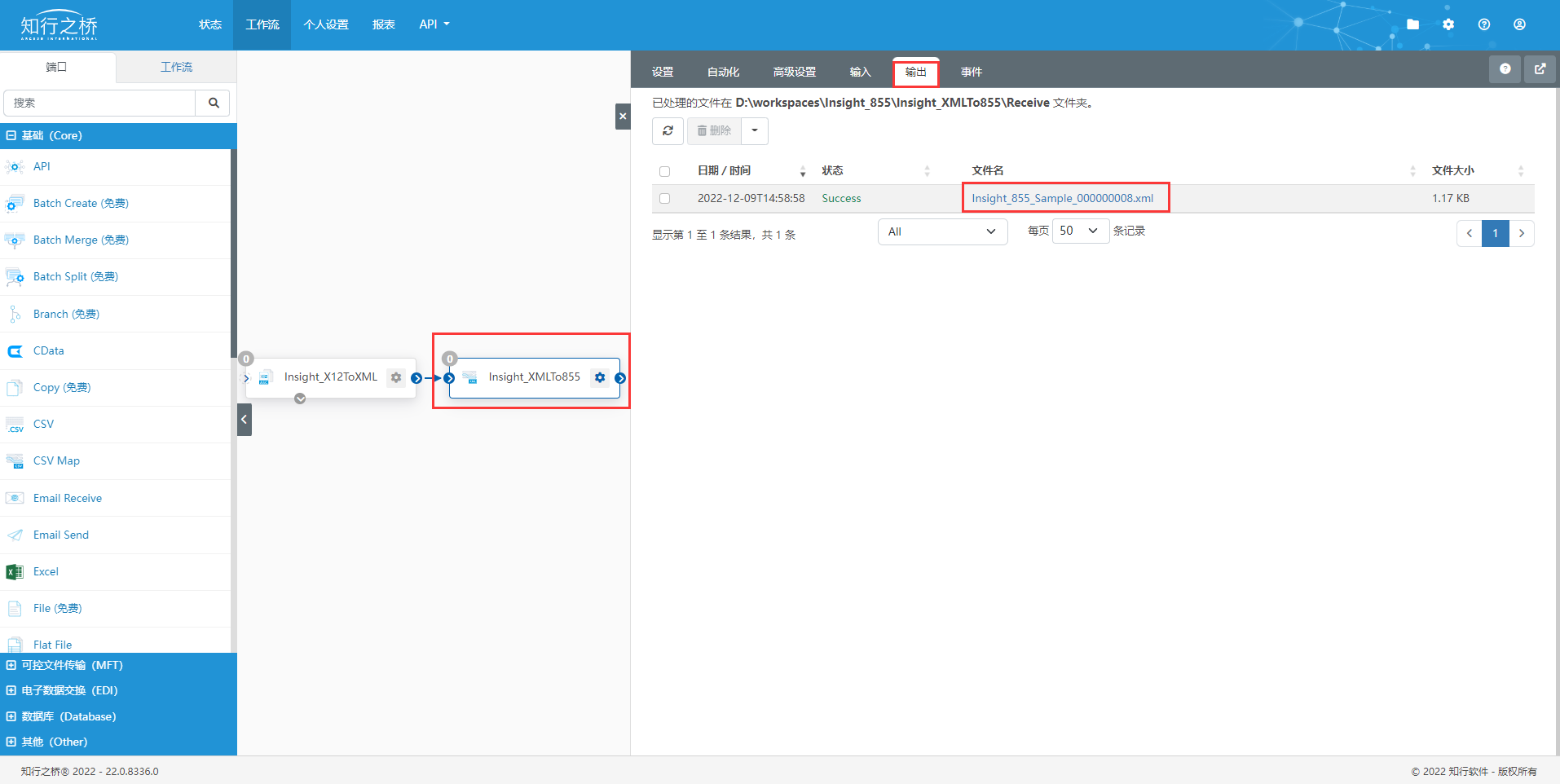
文章目录
- 一 红黑树简介
- 二 探究变色、旋转操作的时机
- 三 总结
一 红黑树简介
- 通过在插入几点时维护数的平衡,这样就不会出现极端情况,使得整棵树的查找效率急剧降低。但是这样造成系统开销过大,因为一旦平衡因子的绝对值超过一就失衡,这样没插入一个节点就可能可能导致失衡。那么有没有一种不能不那么严格的规则来保证平衡?
- 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构。
- 发明者: R u d o l f B a y e r Rudolf Bayer RudolfBayer
- 经典用途是实现关联数组
- 红黑树也是二叉查找树的一种,有红色的结点、有黑色的结点
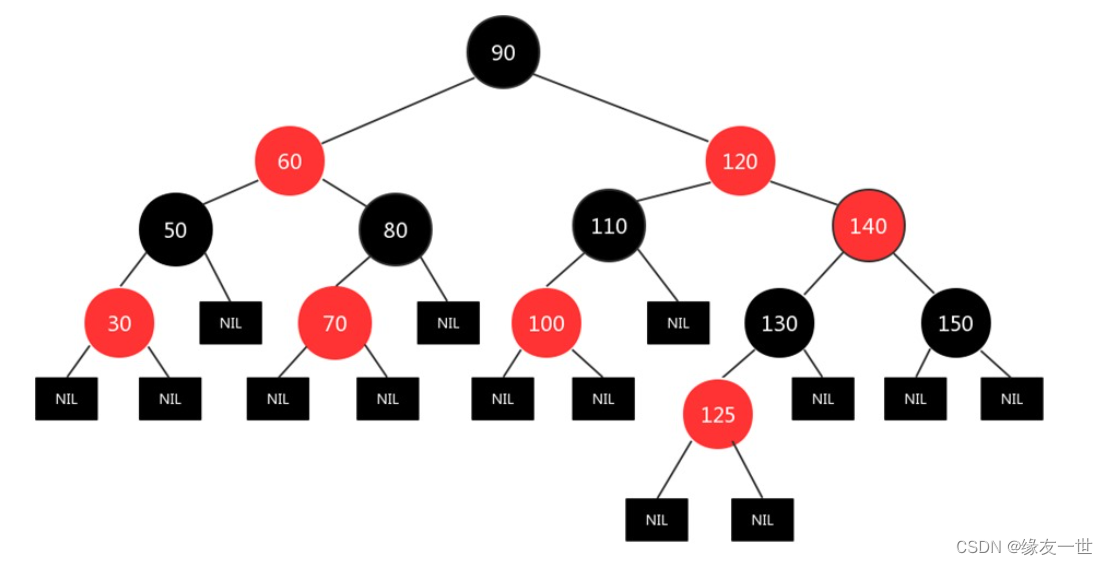
- 红黑树的五大规则
- 每个结点只能黑色或红色的一种
- 根节点一定是黑色
- 红色结点的父节点和子节点不能为红色【红色结点不可以连续】
- 所有空结点【NULL】都是黑色【空结点视为NULL,红黑树中将空结点视为叶子节点】
- 每个结点到叶子结点【空结点(NULL)】路径上出现的黑色节点的个数都相等
二 探究变色、旋转操作的时机
- 根节点为黑色,所以当整个树只有一个根节点的时候,结点的颜色为黑色
- 所有插入的新节点默认情况下是红色
- 默认空结点就不在画出
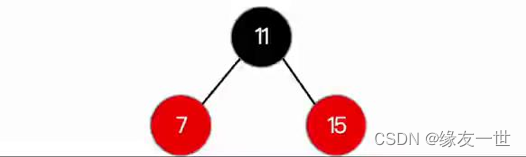
- 插入结点4后,违反红黑树规则 红色结点的父节点和子节点不能为红色【红色结点不可以连续】 红色结点的父节点和子节点不能为红色【红色结点不可以连续】 红色结点的父节点和子节点不能为红色【红色结点不可以连续】
- 变色时机:有些连续的红色结点出现
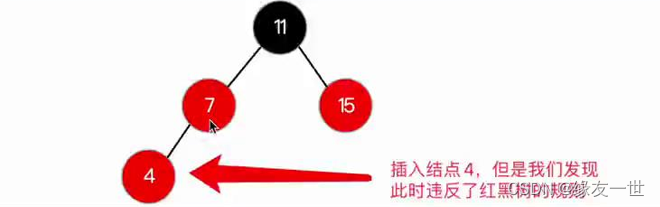
- 所以为了保持红黑树的性质,就需要进行颜色变换。
- 颜色变换:将父节点和父节点的兄弟结点同时变为黑色,然后爷爷结点变为黑色。如果爷爷结点为根节点,就变为黑色,否则,结束。
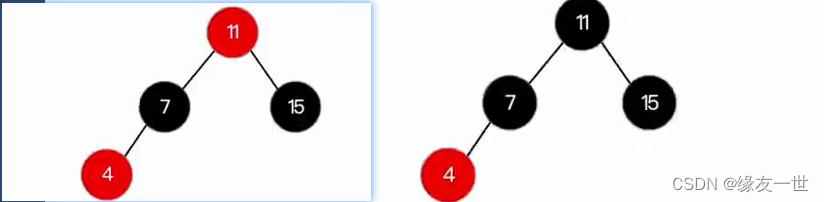
- 继续插入结点
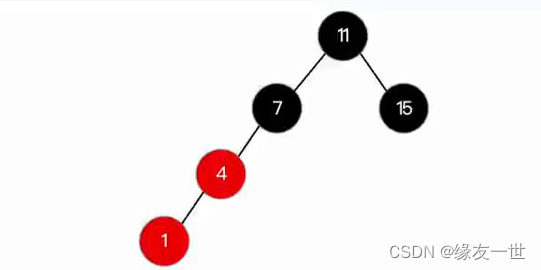
- 出现连续的红色结点,如果进行变色处理的话,无法保证规则5$ 每个结点到叶子结点【空结点(NULL)】路径上出现的黑色节点的个数都相等$
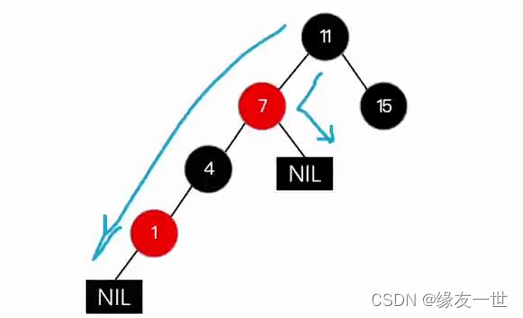
- 旋转操作的时机:对于父节点为红色,父节点的兄弟节点为黑色,变色无法解决问题。
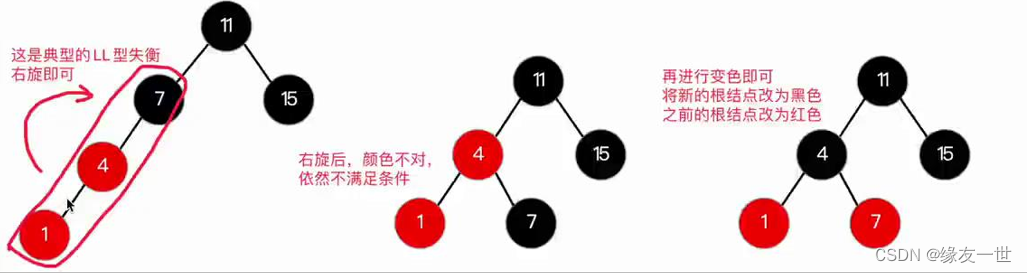
- LL型失衡
- LR型失衡
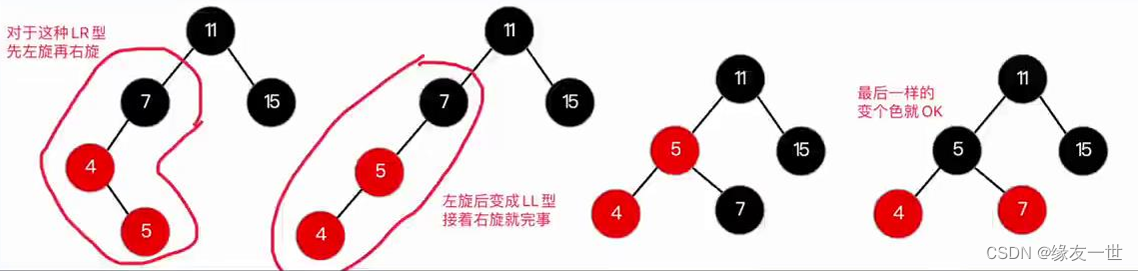
- 注意:旋转和变色的操作顺序可以交换,并没有顺序先后的规定
三 总结
- 插入时的比较判断
- 如果整棵树为NULL直接作为根结点,变成黑色
- 如果父结点是黑色,直接插入即可
- 如果父结点为红色,且父结点的兄弟结点也是红色,直接变色即可(但是注意得继续往上看有没有破坏之前的结构)
- 如果父结点为红色,但父结点的兄弟结点为黑色,需要先根据情况(LL、RR、LR、RL)进行旋转,然后再变色