采用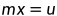 所描述的系统中﹐假设真实质量为m=2,在仿真中,初始值为
所描述的系统中﹐假设真实质量为m=2,在仿真中,初始值为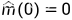 ,采用的自适应律为:
,采用的自适应律为:


设定参数为y=0.5,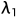 =10,
=10,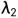 =25,
=25, =6,分别设定参考位置为r(t)=0,r(t )=sin(4t) ,初始条件为
=6,分别设定参考位置为r(t)=0,r(t )=sin(4t) ,初始条件为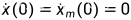 ,
, 。
。
图1.1和图1.2为指令r(t)=0时控制效果,图1.3和图1.4为指令r(t)=sin(4t )时的控制效果。

在本例中,在两种情况下﹐位置跟踪误差收敛到零,而参数估计误差收敛仅适用于后一种情况。第一种情况下,如图1.2所示,参数估计误差不收敛,其原因为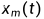 跟踪收敛性能不仅取决于真实的m值。第二种情况下﹐如图1.3所示,由于跟踪指令的频带足够丰富,参数估计误差收敛于真实值,其原因为
跟踪收敛性能不仅取决于真实的m值。第二种情况下﹐如图1.3所示,由于跟踪指令的频带足够丰富,参数估计误差收敛于真实值,其原因为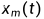 跟踪收敛性能取决于真实的m值。
跟踪收敛性能取决于真实的m值。

在神经网络自适应控制中,神经网络通常用于逼近未知的非线性系统。基于同样的原因逼近误差的收敛性往往无法实现,但这不影响闭环系统的稳定性。图1.4为r(t)=sin(4t)时未知负载的参数估计,此时m=2。

仿真图

控制设计主程序(chap_1ctrl.m)
function [ sys, x0 , str,ts] = spacemodel( t,x, u, flag)switch flag,
case 0,
[ sys, x0 , str,ts ] = mdlInitializeSizes;
case 1,
sys = mdlDerivatives(t,x, u);
case 3,
sys = mdlOutputs( t,x, u);
case { 2,4,9}
sys = [ ];
otherwise
error( [ 'Unhandled flag = ', num2str( flag)]);
end
function[ sys,x0 , str,ts ] = mdlInitializeSizessizes =simsizes;
sizes. NumContStates= 1;
sizes. NumDiscstates= 0 ;
sizes.NumOutputs= 2 ;
sizes. DirFeedthrough= 1 ;
sizes. NumInputs=6
sizes.NumSampleTimes= 0;
sys = simsizes( sizes) ;
x0= [ 0];
str = [ ]; ts = [ ];
function sys = mdlDerivatives(t,x, u)
xm = u( 1) ;
dxn = u(2);
ddxm = u( 3) ;
xl = u( 4);
dx1 = u( 5);
e = x1- xm;
de = dx1 - dxm ;
nmn = 6 ;
s = de+nmn * e;
v = ddxm- 2*nmn*de - nmn ^2*e;
gama = 0.5;
sys(1) = - gama * v* s ;
function sys = mdlOutputs( t,x,u)xm = u( 1);
dxm = u( 2);
ddxm = u( 3) ;
xl = u(4 ) ;dxl = u(5);
e = x1- xm;
de = dx1 - dxm;
nmn = 6;
mp = x( 1);
ut= mp * ( ddxm - 2*nmn * de - nmn ^2 * e) ;
sys(1)= mp;
sys(2) = ut;
被控对象程序(chap_1plant.m)
function [ sys,x0 , str,ts] = spacemodel ( t,x, u,flag)
switch flag
case 0,
[ sys,x0 ,str,ts ] = mdlInitializeSizes;
case 1,
sys = mdlDerivatives( t,x, u);
case 3,
sys = mdlOutputs(t,x, u) ;
case {2,4,9 }
sys =[ ];
otherwise
error( [ 'Unhandled flag = ' , num2str( flag)]);
end
function [ sys, x0 , str,ts ] = mdlInitializeSizes
sizes = simsizes;
sizes. NumContStates
= 2;
sizes. NumDiscStates
= 0;
sizes. NumOutputs
= 3;
sizes.NumInputs
= 2;
sizes. DirFeedthrough
= 0 ;
sizes. NumSampleTimes= 1;sys = simsizes( sizes) ;
x0 =[ 0.5,0];
str = [ ]; ts = [ 0 0];
function sys = mdlDerivatives( t,x, u)m= 2;
ut = u( 2);
sys( 1) = x( 2);
sys(2)= 1/m * ut;
function sys = mdlOutputs( t,x, u)
m= 2;
sys( 1) = x(1);
sys(2) = x( 2);
sys( 3) = m;
指令信号程序(chap_linpot.m)
function [ sys, x0 , str,ts] = spacemodel ( t,x, u, flag)
switch flag,
case 0,
[ sys, x0 , str,ts ] = mdlInitializeSizes;
case 1,
sys = mdlDerivatives(t,x, u);
case 3,
sys = mdlOutputs(t,x,u) ;
case {2,4,9}
sys = [ ];
otherwise
error( [ 'Unhandled flag = ' , num2str( flag) ]);
end
function [ sys,x0 , str,ts] = mdlInitializeSizes
global M
M= 2;
sizes = simsizes
sizes. NumDiscStates=0 ;
sizes.NumOutputs= 3;
sizes. NumInputs= 0 ;
sizes.DirFeedthrough= 1 ;
sizes. NurmSampleTimes= 0 ;
sys = simsizes(sizes) ;
x0= [ 0.5,0];
str = [ ];ts = [ ];
function sys = mdlDerivatives( t,x, u)
global M
if M== 1
r = 0;
elseif M == 2
r = sin( 4 * t);
end
nmn1 = 10;
nmn2 = 25;
sys( 1) = x( 2);
sys(2) = - nmn1 * x( 2) - nmn2 * x( 1) + nmn2 * r;
function sys = mdloutputs( t,x, u)
global M
if M== 1r = 0;
elseif M == 2r = sin( 4 * t);end
nmn1 = 10;nmn2= 25;
xm = x( 1) ;dxm = x( 2);
ddxm = - nmn1 * x( 2) - nmn2 * x(1) + nmn2 * r;
sys( 1) = xm ;
sys(2) = dxm;
sys( 3) = ddxm ;
画图程序(chap_1plot.m)
close all;
f igure( 1);
plot( t,y( : ,1 ) ,'r',t,y( :,4),'k: ", 'linewidth',2);xlabel( 'time(s) ') ;
ylabel( 'position signal ' );
legend( 'ideal position signal' , 'position tracking' );
figure(2);
plot(t,p( :,3) , 'r ',t,p( :,4), 'k : ', 'linewidth',2);xlabel( 'time(s) ' ) ;
ylabel( 'estimation value' );
legend( 'True value,m ' , 'estimation value' ) ;