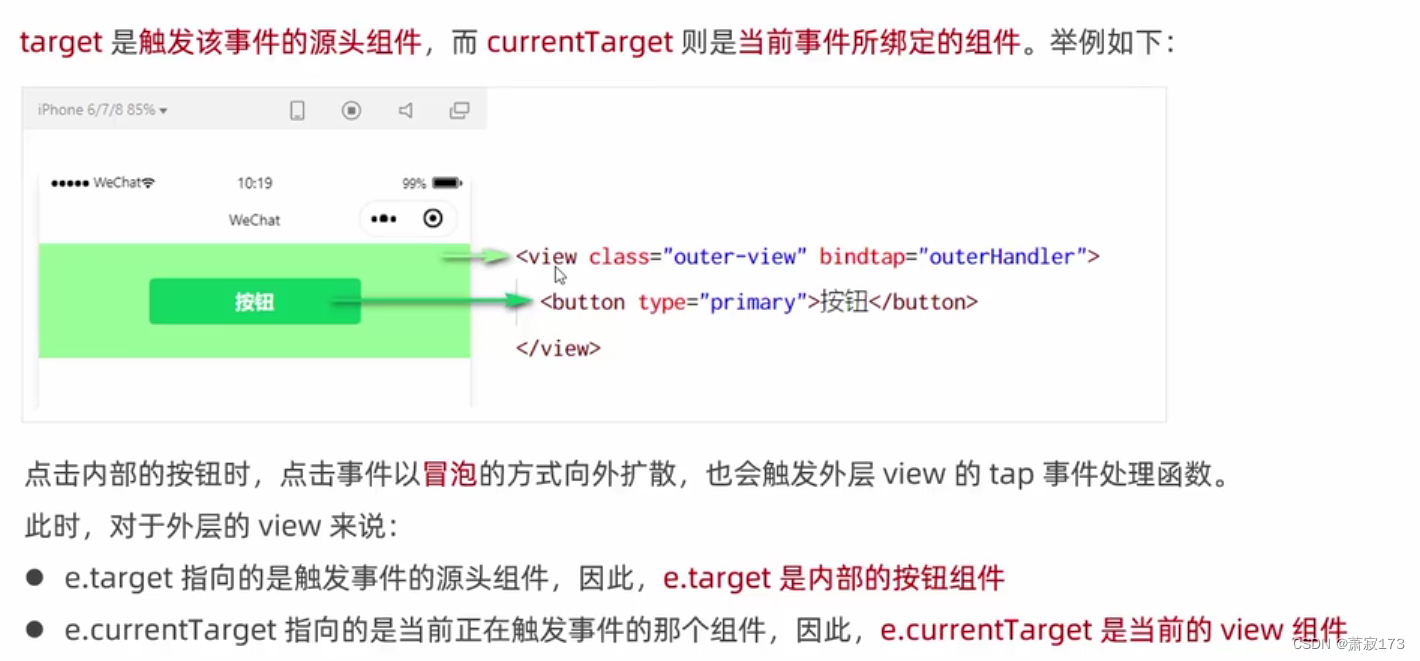
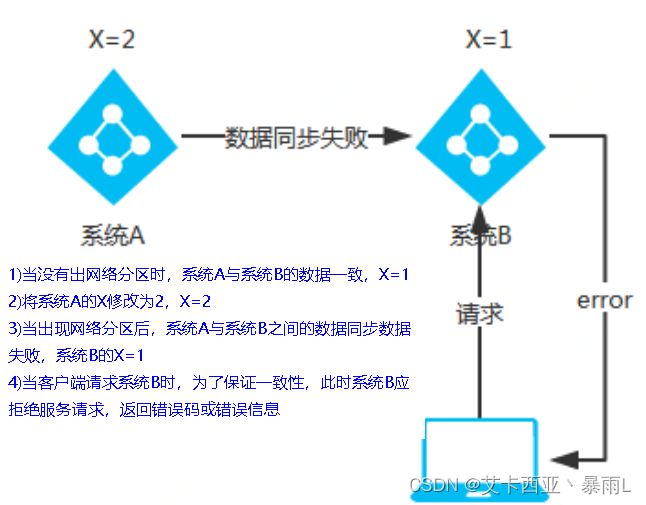
今天学习了链式向前星和唯一分解定理(数论)。
链式向前星
链式向前星是一种存储图的方法,在此之前我们学到过存储图的方式:邻接表以及邻接矩阵,邻接矩阵浪费了很大的空间,而邻接表 写起来的代码有一点点的麻烦,这里的链式向前星,我认为是用数组链表静态模拟了一个链表。
结构体的大小是根据边的大小来设置的
它的结构体如下:

其中 edges 里面的to 代表的是当前边到达的顶点,就是我们输入u,v,w里面的v值;
而w就是u,w,v里面的w;next是当前已经输入的边当中,和u同起点的上一条输入的边。
我们怎么知道和u同起点的上一条已经输入过的边?
我们需要借助一个数组:
![]()
该数组记录的是每一个顶点,最后访问到的边,我们通常不以0作顶点,所以该数组里面初始化会是0,如果你是从0作顶点,那么就需要初始化为-1.
然后就是输入咯

输入终点和权值只需要记下来,edges[i].next=head[u],就是代表与u同顶点的前一条边,然后需要把刷新与u同起点的边的值,因为我们以及输入了一个以u为起点的一条边,当前输入的是第几条边,那么我们就可以直接赋值。
最后直接输出即可

C代码如下:

#include<stdio.h>
#define N 100
#define M 100
int n,m;
struct node
{
int to;
int w;
int next;
}edges[M];
int head[N];
int main()
{
int i,j,u,v,w;
puts("请输入你的顶点数:");
scanf("%d",&n);
puts("请输入你的边的总数:");
scanf("%d",&m);
puts("请输入起点、终点以及权值:");
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
edges[i].to=v;
edges[i].w=w;
edges[i].next=head[u];
head[u]=i;
}
/* for(i=1;i<=m;i++)
{
printf("%d %d %d\n",edges[i].to,edges[i].w,edges[i].next);
}
for(i=1;i<=n;i++)
{
printf("%d ",head[i]);
}*/
for(i=1;i<=n;i++)
{
printf("%d能到达的边:",i);
for(j=head[i];j!=0;j=edges[j].next)
{
printf("%d ",edges[j].to);
}
puts("");
}
}C++代码如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
const int N=100;
const int M=100;
int n,m;
struct node
{
int to;
int w;
int next;
}edges[M];
int head[N];
int main()
{
int i,j,u,v,w;
cout << "请输入你的顶点数:" << endl;
cin >> n ;
cout << "请输入你的边的总数:" << endl;
cin >> m ;
cout << "请输入起点、终点以及权值:" << endl;
for(i=1;i<=m;i++)
{
cin >> u >> v >> w ;
edges[i].to=v;
edges[i].w=w;
edges[i].next=head[u];
head[u]=i;
}
for(i=1;i<=n;i++)
{
cout << i << "能到达的边:" << endl;
for(j=head[i];j!=0;j=edges[j].next)
{
cout << edges[j].to << " " ;
}
cout << endl ;
}
return 0;
}
唯一分解定理
唯一分解定理又称算术基本定理,指:一个大于一的正整数N都可以唯一分解成有限个质数的乘积。N=p1^a1*p2^a2*p3^a3*...*pn^an,这里p1<p2<p3<...<pn均为质数,ai均为正整数.
这样的分解称为N的标准分解式.(听起来有点类似于哥德巴赫猜想)
该题主要用在求N的因子个数,找最大公约数以及最小公倍数。
求N的因子个数:
我们来假设12,12的素数因子有2,3
12=(2^2)*(3^1)
它的因子个数就等于各位素数的幂次+1相乘起来
即:(2+1)*(1+1)=6
12的因子有 1,2,3,4,6,12一共6个。
求最大公约数以及最小公倍数:
这里是9 和12(取素数的时候我们,需要将每个存在于一方的素数,化成到俩方都有)
比如下面这个,本来9分解出来是没有素数2的,但是12,有,我们只需要写上2^0即可,不影响结果
9=(2^0)*(3^2)
12=(2^2)*(3*1)
最小公约数:
gcd(9,12)=2^(min(0,2))*3^(min(1,2))=3
lcm(9,12)= 2^(max(0,2))*3^(max(1,2))=36