激活函数:GELU(Gaussian Error Linear Units)
- 前言
- 相关介绍
- GELU(Gaussian Error Linear Units)
- 代码示例
- 参考

前言
- 由于本人水平有限,难免出现错漏,敬请批评改正。
- 更多精彩内容,可点击进入人工智能知识点专栏、Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看
- 基于DETR的人脸伪装检测
- YOLOv7训练自己的数据集(口罩检测)
- YOLOv8训练自己的数据集(足球检测)
- YOLOv5:TensorRT加速YOLOv5模型推理
- YOLOv5:IoU、GIoU、DIoU、CIoU、EIoU
- 玩转Jetson Nano(五):TensorRT加速YOLOv5目标检测
- YOLOv5:添加SE、CBAM、CoordAtt、ECA注意力机制
- YOLOv5:yolov5s.yaml配置文件解读、增加小目标检测层
- Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集
- YOLOv5:使用7.0版本训练自己的实例分割模型(车辆、行人、路标、车道线等实例分割)
- 使用Kaggle GPU资源免费体验Stable Diffusion开源项目
相关介绍
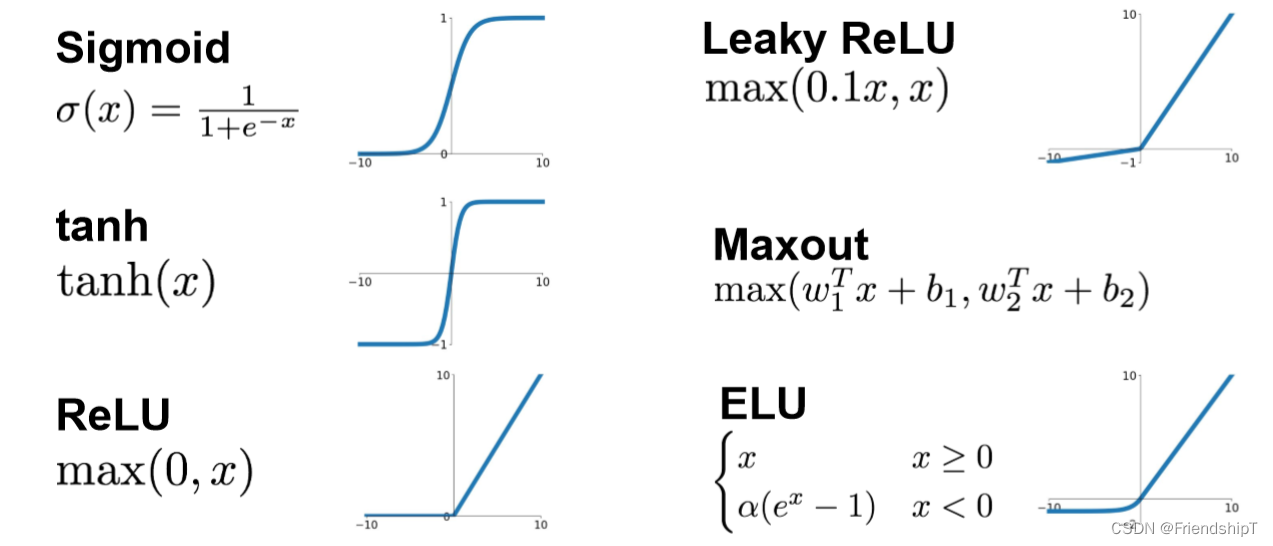
激活函数在神经网络中起着至关重要的作用,它是神经网络模型中的非线性转换组件,用于引入非线性特性到模型中,使得神经网络能够学习和表达复杂的数据分布和模式。下面是几个常见的激活函数及其特点:
-
sigmoid函数:
- 数学表达式:σ(x) = 1 / (1 + e^(-x))
- 输出范围:(0, 1),将输入映射到0和1之间,常用于二元分类问题的输出层,因其输出可以解释为概率。
- 缺点:sigmoid函数在两端饱和区的梯度几乎为0,这可能导致梯度消失问题,不利于网络的深层训练。
-
tanh(双曲正切函数):
- 数学表达式:tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
- 输出范围:(-1, 1),与sigmoid类似,也是饱和函数,但输出中心位于0,更适合于数据标准化后的情况。
- 同样存在饱和区梯度消失的问题。
-
ReLU(Rectified Linear Unit):
- 数学表达式:ReLU(x) = max(0, x)
- 输出范围:(0, +∞),当输入大于0时,函数输出等于输入,输入小于0时,输出为0。
- 优点:解决了sigmoid和tanh函数的梯度消失问题,大大加快了神经网络的训练速度。
- 缺点:在负值区域的梯度为0,可能导致神经元死亡(dead ReLU问题)。
-
Leaky ReLU(Leaky Rectified Linear Unit):
- 改进了ReLU,对负值区域赋予一个小的非零斜率,如Leaky ReLU(x) = max(ax, x),其中a是常数,通常很小(如0.01)。
- 解决了ReLU在负半轴无梯度的问题。
-
ELU(Exponential Linear Units):
- 数学表达式:ELU(x) = max(0, x) + min(0, α * (e^x - 1))
- ELU在x>0时的行为与ReLU相似,而在x<0时具有连续的负梯度,有助于在网络中维持均值为0的激活值分布。
-
Swish:
- Swish函数是由Google Brain团队提出的一种自门控激活函数,表达式为:swish(x) = x * sigmoid(x)。
- Swish在很大程度上克服了ReLU家族存在的问题,具有更好的训练表现和理论优势。
-
GELU(Gaussian Error Linear Units):
- GELU函数尝试模拟自然神经元的行为,它结合了线性部分和非线性部分,具有较好的理论依据和实际效果。
激活函数的选择取决于具体的应用场景和模型需求,需考虑训练效率、模型表达能力、梯度流等因素。随着深度学习研究的发展,还出现了更多新型激活函数,如SELU、Mish等。
GELU(Gaussian Error Linear Units)
GELU(Gaussian Error Linear Units)是一种激活函数,由Hendrycks和Gimpel在2016年的论文《Gaussian Error Linear Units (GELUs)》中提出,它旨在改善现有激活函数如ReLU在神经网络中的表现,尤其是对于那些追求更好性能和收敛速度的深层网络。
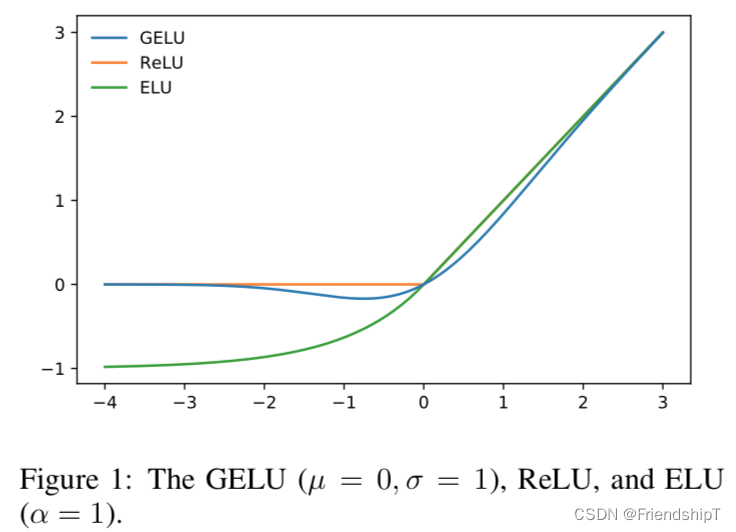
GELU的基本概念:
GELU的设计灵感来自于随机神经网络和高斯误差函数,它试图模仿自然神经元的行为,即输入信号与噪声的交互。GELU的公式可以表示为:
G E L U ( x ) = x ⋅ Φ ( x ) = x ⋅ P ( X ≤ x ) , 其中 X ∼ N ( 0 , 1 ) GELU(x) = x \cdot \Phi(x) = x \cdot P(X \leq x), \text{其中} \quad X \sim \mathcal{N}(0, 1) GELU(x)=x⋅Φ(x)=x⋅P(X≤x),其中X∼N(0,1)
其中,( Phi(x) ) 是标准正态分布的累积分布函数(CDF),( x ) 是神经网络中某个神经元的线性输入。这意味着GELU激活函数在输入值较小时给出较小的非线性响应,随着输入值增大,非线性响应逐渐增强,同时保持了负输入区域的部分响应,这一点不同于ReLU,后者在输入小于0时输出恒为0。
GELU的优势:
-
平滑性:相比于ReLU及其变种,GELU函数在整个实数域上是连续且光滑的,这有助于在训练过程中梯度更容易传播,进而提高模型的训练效率和收敛速度。
-
饱和度控制:GELU在较大输入时不会像sigmoid那样饱和,也不会像ReLU那样在大于0的区域产生恒定斜率,而是根据输入值的大小提供不同的非线性程度。
-
减少过拟合:GELU的随机性和对输入分布的适应性有助于减轻过拟合现象,使得模型在处理复杂任务时表现更好。
GELU缺点和挑战:
-
计算效率:GELU函数不像ReLU那样易于计算,因为它不是简单的阈值函数。为了计算GELU,可以直接使用公式,但该公式涉及到误差函数(erf),在某些计算平台或硬件上可能没有直接的硬件支持,导致计算相对复杂和耗时。为此,常常需要使用近似方法来提高计算效率。
-
近似误差:在实际应用中,由于 erf 函数的复杂性,通常会使用近似公式替代,这可能导致某种程度上的精度损失。尽管这种损失在大多数情况下影响不大,但在极端情况下可能会有一定的影响。
-
初始化敏感性:GELU相对于ReLU等函数可能对模型权重的初始值更为敏感,不当的初始化可能会导致训练初期梯度消失或爆炸的问题。
-
理解和调试难度:由于GELU函数的复杂性,对于开发者和研究者来说,理解和调试网络中使用GELU的地方可能比使用简单函数(如ReLU)更具挑战性。
然而,尽管存在这些潜在的缺点,GELU仍然在很多深度学习模型中取得了良好的效果,特别是在大型预训练模型中,它的优势往往超过其带来的计算复杂性等挑战。随着计算资源和硬件优化的不断提升,这些问题的影响也在逐渐减弱。
实际应用:
GELU在现代深度学习模型中,尤其是在BERT、RoBERTa、ALBERT等先进的自然语言处理模型以及图像处理和其他领域的一些深度神经网络中得到广泛应用。GELU的使用有助于提升模型的性能,尤其是在具有大量参数和深层结构的模型中。
代码示例
以下是一个使用PyTorch实现GELU激活函数的例子,包括如何定义一个带有GELU激活层的简单神经网络模型,并进行一次前向传播计算:
import torch
import torch.nn as nn
from torch.nn.functional import gelu
# 定义GELU激活函数
def custom_gelu(x):
return x * torch.sigmoid(1.702 * x)
# 使用内置的GELU函数
# class CustomLayer(nn.Module):
# def __init__(self):
# super(CustomLayer, self).__init__()
# def forward(self, x):
# return gelu(x)
# 使用自定义的GELU实现
class CustomLayer(nn.Module):
def __init__(self):
super(CustomLayer, self).__init__()
def forward(self, x):
return custom_gelu(x)
# 创建一个简单的网络模型,包含一个线性层和一个GELU层
model = nn.Sequential(
nn.Linear(10, 20), # 输入维度为10,输出维度为20
CustomLayer(),
)
# 创建一个随机输入张量
input_data = torch.randn(10, 10) # 假设我们有10个样本,每个样本有10个特征
# 将输入数据传递给模型进行前向传播
output = model(input_data)
# 输出结果
print(output.shape) # torch.Size([10, 20])
在这个例子中,我们首先导入了所需的PyTorch库,然后定义了一个自定义的GELU函数。虽然PyTorch提供了内置的torch.nn.functional.gelu函数,但我们同样展示了如何自定义实现GELU激活函数。
接下来,我们定义了一个简单的神经网络模型,模型包含一个线性层(nn.Linear)和一个应用了GELU激活函数的层(CustomLayer)。然后,我们创建了一个随机张量作为输入数据,并将其通过模型进行前向传播计算,最后输出了经过GELU激活函数处理后的结果张量的形状。
参考
[1] Dan Hendrycks, Kevin Gimpel. Gaussian Error Linear Units (GELUs). 2016
- 由于本人水平有限,难免出现错漏,敬请批评改正。
- 更多精彩内容,可点击进入人工智能知识点专栏、Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看
- 基于DETR的人脸伪装检测
- YOLOv7训练自己的数据集(口罩检测)
- YOLOv8训练自己的数据集(足球检测)
- YOLOv5:TensorRT加速YOLOv5模型推理
- YOLOv5:IoU、GIoU、DIoU、CIoU、EIoU
- 玩转Jetson Nano(五):TensorRT加速YOLOv5目标检测
- YOLOv5:添加SE、CBAM、CoordAtt、ECA注意力机制
- YOLOv5:yolov5s.yaml配置文件解读、增加小目标检测层
- Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集
- YOLOv5:使用7.0版本训练自己的实例分割模型(车辆、行人、路标、车道线等实例分割)
- 使用Kaggle GPU资源免费体验Stable Diffusion开源项目