定义
- G = (V, E) 图 = (点,边)
图,Graph
点,Vertex
边,edge
有空表,空树,但没有空图
图可以没有边|E| = 0,但不能没有一个点
- 稠密图 &稀疏图
是边的多少决定的
- (见Excel对照表)
- 例题
无向图,23条边,度为4的有5个点,度为3的有4个点,度为2的有多少个点?
无向图的度总数 = 每个点的度数之和 = 2倍的边数
23x2 = 4x5 + 3x4 + 2xN,N = 7
图的存储
- (根据各个表示法,还原成图)
- (根据图写出各个表示法)
图的遍历
- 广度优先BFS
队列
- 深度优先DFS
栈
深度优先递归遍历一个无环的,有向图,只在退出时输出相应的点,这样,得到的顶点序列,是逆拓扑排序(王道.P210.T11)
图的应用
不可以检查,有向图是否构成环(回路):最短路径的3个方法,广迪弗(甘道夫)
知识点对比学习
图的基本概念
| 简单图 | 1、不存在重复边 2、不存在顶点到自身的边 | |
| 多重图 | 不是简单图 | |
| 连通 | 任意两点都有路径存在 | |
| 路径 | 点到点的一些顶点序列 | |
| 路径长度/距离 | 边的数量 | |
| 回路=环 | 1、起点和终点相同的路径 2、有回路,无拓扑序列 | 回路≠简单路径(40811.T8) |
| 简单路径 | 顶点不重复出现的路径 | |
| 简单回路 | 简单路径的回路 |
有向图 & 无向图
| 无向图 | 有向图 | ||
| 1、任意两点之间都存在1个边 2、一共有 Cn2 = n(n-1)/2 条边 | 完全图 | 有向完全图 | 1、任意两点之间都存在2个边,一来一回 2、一共有 2Cn2 = n(n-1) 条边 3、其中一个顶点最多可有 2n-2 的度(王道P191.T9) |
| n是点的个数 1、连通图最少有 n-1 条边(+1就可成环) 2、非连通图最多有 Cn-12 条边 3、在任何情况下都是连通的(=非连通最多边数+1)则要Cn-12 + 1(408.10.T7) | 连通图 任意点2点都有路径 | 强连通图 | 1、点A到点B有路径,且点B到点A有路径,则这两点才是强联通的 2、任意两点强连通,则是强连通图 3、最少有 n 条边,构成一个环 |
| 1、尽可能多得顶点和边 P189.图6.2.ab | 连通分量 极大连通子图 | 强连通分量 极大强连通子图 | |
| 1、度 = 2e = 每个点的度数的和(王道P191.T8/P192.T18) 2、2倍的边长,每条边都有2个顶点相连 | 度 n点e边 | TD = ID + OD | 1、总度 = 入度 + 出度 入度:箭头指向顶点,顶点作为终点 出度:顶点作为起点 2、入度 = 出度 = e 3、每条有向边都有一个起点和终点 |
| 1、全部点,极少边(极小连通子图) 2、n 个点,则 n-1 条边 | 生成树 | ||
| 由各个单独的连通分量构成生成树的集合 | 生成森林 |
| Cn2的意思是,n个边,任意选2个,不重复的边的个数 An2的意思是,n个边,任意选2个,可重复选 |
图的存储
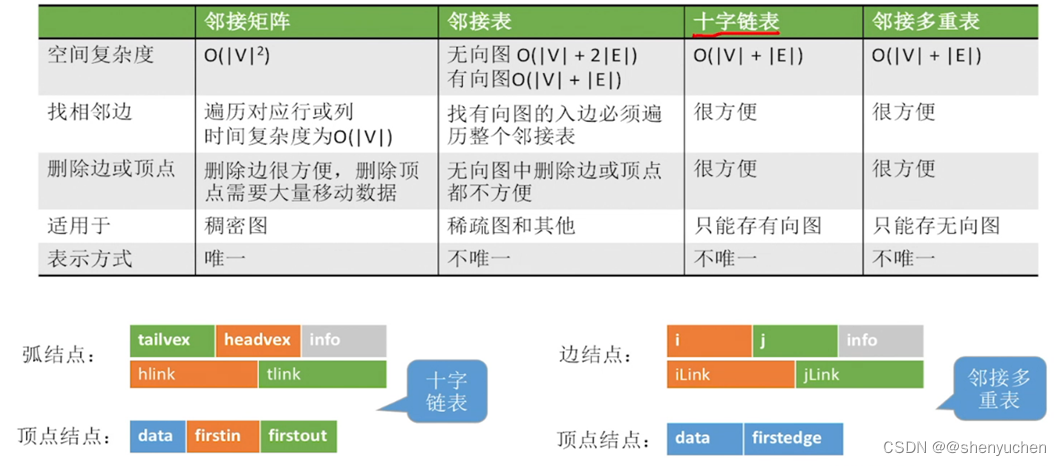
| 图的存储 | 邻接矩阵 (类似线代中的矩阵,是个矩形) | 邻接表 | 十字链表 | 邻接多重表 |
| 空间复杂度 | O( |V|2 ) | 无向图:O( |V| + 2|E| ) 有向图:O( |V| + |E| ) | O( |V| + |E| ) | O( |V| + |E| ) |
| 适用于 | 稠密图 | 稀疏图 | 只能有向图 | 只能无向图 |
| 表示方式 (存图的结果) | 唯一 “生成树/森林”也唯一 | 不唯一 “生成树/森林”不唯一 | ||
| 常考点 | 1、存储大小只和顶点有关 2、无向图的度 = 一行/一列 有向图的度 = 出度(一行) + 入度(一列) | 1、出度:一行 入度:扫描整个表 | ||