面试经典算法32 - 验证二叉树
LeetCode.98
公众号:阿Q技术站
问题描述
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
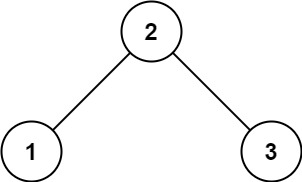
输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
思路
为了判断一个二叉树是否是有效的二叉搜索树,可以利用二叉搜索树的性质:对于每个节点,其左子树的所有节点都小于当前节点,右子树的所有节点都大于当前节点。同时,左右子树也必须分别是有效的二叉搜索树。
递归
- 定义一个辅助函数
isValidBSTHelper,用于递归判断以当前节点为根的子树是否是有效的二叉搜索树。 - 在辅助函数中,传入当前节点、允许的最小值和最大值。
- 如果当前节点为空,说明是有效的二叉搜索树,返回 true。
- 如果当前节点的值不在最小值和最大值的范围内,说明不是有效的二叉搜索树,返回 false。
- 递归判断左子树和右子树,左子树的最大值为当前节点的值,右子树的最小值为当前节点的值。
- 如果左子树和右子树都是有效的二叉搜索树,则当前节点也是有效的二叉搜索树,返回 true。
非递归
- 使用栈来模拟中序遍历的过程,从根节点开始,先将左子节点依次入栈,直到最左下的叶子节点。
- 弹出栈顶节点,判断其值是否大于前一个节点的值(如果存在)。如果不满足递增关系,则不是有效的二叉搜索树,返回 false。
- 将当前节点的右子节点入栈,继续遍历右子树。
- 重复步骤 2 和步骤 3,直到栈为空且所有节点都遍历完毕。
图解
- 创建空栈
s和当前节点指针curr,初始化prev为long类型最小值
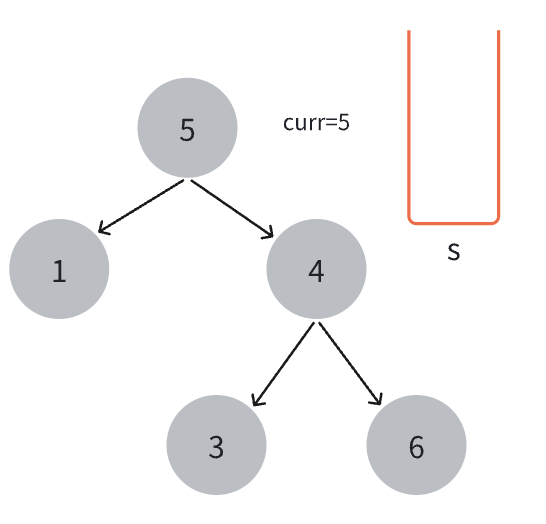
- 如果当前节点不为空或栈不为空,则将当前节点入栈,然后将当前节点指向其左子节点,重复此步骤直到当前节点为空。

- 如果当前节点为空,说明已经到达最左下角的节点,将栈顶节点弹出。

- 栈顶元素的值不小于long类型的最小值。将
prev更新为当前节点值。
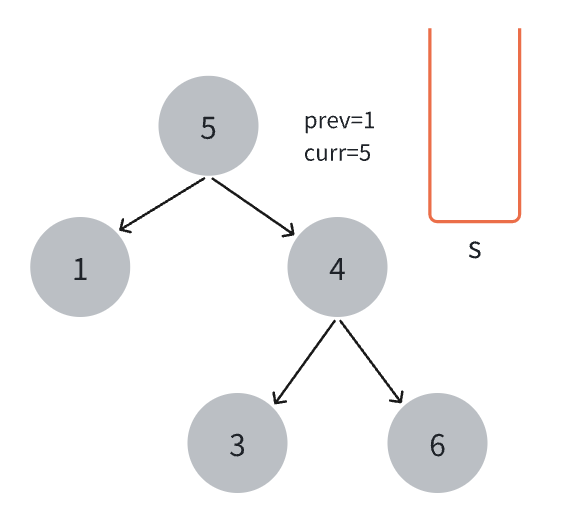
- 处理右子节点。
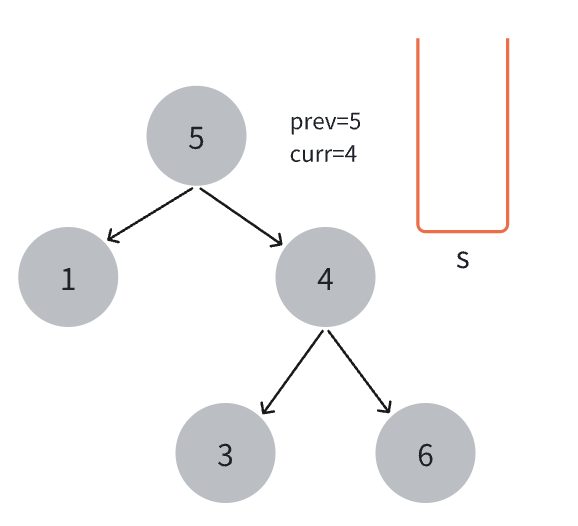
此时,当前节点值小于前一个节点的值,说明不是二叉搜索树,返回 false。
参考代码
C++
递归
#include <iostream>
#include <limits>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
bool isValidBST(TreeNode* root) {
return isValidBSTHelper(root, numeric_limits<long>::min(), numeric_limits<long>::max());
}
private:
bool isValidBSTHelper(TreeNode* root, long minVal, long maxVal) {
if (!root) {
return true; // 空节点是有效的二叉搜索树
}
if (root->val <= minVal || root->val >= maxVal) {
return false; // 当前节点的值不在允许的范围内,不是有效的二叉搜索树
}
// 递归判断左子树和右子树
return isValidBSTHelper(root->left, minVal, root->val) && isValidBSTHelper(root->right, root->val, maxVal);
}
};
// 创建二叉树
TreeNode* createTree(vector<int>& nodes, int index) {
if (index >= nodes.size() || nodes[index] == -1) {
return nullptr; // 如果节点为空,则返回nullptr
}
TreeNode* root = new TreeNode(nodes[index]); // 创建当前节点
root->left = createTree(nodes, 2 * index + 1); // 创建左子树
root->right = createTree(nodes, 2 * index + 2); // 创建右子树
return root; // 返回当前节点
}
int main() {
vector<int> nodes = {2, 1, 3}; // 二叉搜索树的中序遍历序列
TreeNode* root = createTree(nodes, 0); // 创建二叉树
Solution solution;
bool result = solution.isValidBST(root); // 判断二叉树是否是有效的二叉搜索树
cout << (result ? "true" : "false") << endl; // 输出结果
return 0;
}
非递归
#include <iostream>
#include <stack>
#include <limits>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> s; // 辅助栈,用于模拟中序遍历过程
TreeNode* curr = root; // 当前节点
long prev = numeric_limits<long>::min(); // 用于保存前一个节点的值,初始化为 long 类型最小值
while (curr || !s.empty()) {
while (curr) {
s.push(curr); // 将当前节点入栈
curr = curr->left; // 遍历左子树
}
curr = s.top(); // 获取栈顶节点
s.pop(); // 弹出栈顶节点
if (curr->val <= prev) {
return false; // 如果当前节点值小于等于前一个节点的值,说明不是二叉搜索树,返回 false
}
prev = curr->val; // 更新前一个节点的值为当前节点的值
curr = curr->right; // 处理右子节点
}
return true; // 遍历完所有节点,返回 true
}
};
// 创建二叉树
TreeNode* createTree(vector<int>& nodes, int index) {
if (index >= nodes.size() || nodes[index] == -1) {
return nullptr; // 如果节点为空,则返回nullptr
}
TreeNode* root = new TreeNode(nodes[index]); // 创建当前节点
root->left = createTree(nodes, 2 * index + 1); // 创建左子树
root->right = createTree(nodes, 2 * index + 2); // 创建右子树
return root; // 返回当前节点
}
int main() {
vector<int> nodes = {2, 1, 3}; // 二叉搜索树的中序遍历序列
TreeNode* root = createTree(nodes, 0); // 创建二叉树
Solution solution;
bool result = solution.isValidBST(root); // 判断二叉树是否是有效的二叉搜索树
cout << (result ? "true" : "false") << endl; // 输出结果
return 0;
}
Java
import java.util.Stack;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack = new Stack<>(); // 辅助栈,用于模拟中序遍历过程
TreeNode curr = root; // 当前节点
long prev = Long.MIN_VALUE; // 用于保存前一个节点的值,初始化为 long 类型最小值
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr); // 将当前节点入栈
curr = curr.left; // 遍历左子树
}
curr = stack.pop(); // 获取栈顶节点
if (curr.val <= prev) {
return false; // 如果当前节点值小于等于前一个节点的值,说明不是二叉搜索树,返回 false
}
prev = curr.val; // 更新前一个节点的值为当前节点的值
curr = curr.right; // 处理右子节点
}
return true; // 遍历完所有节点,返回 true
}
}
public class Main {
public static void main(String[] args) {
TreeNode root = new TreeNode(2);
root.left = new TreeNode(1);
root.right = new TreeNode(3);
Solution solution = new Solution();
boolean result = solution.isValidBST(root); // 判断二叉树是否是有效的二叉搜索树
System.out.println(result); // 输出结果
}
}
Python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
stack = [] # 辅助栈,用于模拟中序遍历过程
curr = root # 当前节点
prev = float("-inf") # 用于保存前一个节点的值,初始化为负无穷
while curr or stack:
while curr:
stack.append(curr) # 将当前节点入栈
curr = curr.left # 遍历左子树
curr = stack.pop() # 获取栈顶节点
if curr.val <= prev:
return False # 如果当前节点值小于等于前一个节点的值,说明不是二叉搜索树,返回 False
prev = curr.val # 更新前一个节点的值为当前节点的值
curr = curr.right # 处理右子节点
return True # 遍历完所有节点,返回 True
# 创建二叉树
root = TreeNode(2)
root.left = TreeNode(1)
root.right = TreeNode(3)
solution = Solution()
result = solution.isValidBST(root) # 判断二叉树是否是有效的二叉搜索树
print(result) # 输出结果






![[Qt网络编程]之UDP通讯的简单编程实现](https://img-blog.csdnimg.cn/direct/83cc742e09474071862b6b8db63aa3b6.png)