Swin Transformer 浅析
文章目录
- Swin Transformer 浅析
- 引言
- Swin Transformer 的网络结构
- W-MSA 窗口多头注意力机制
- SW-MSA 滑动窗口多头注意力机制
- Patch Merging 图块合并
引言
因为ViT无法实现CNN中的层次化构建以及局部信息,由此微软团队提出了Swin Transformer来解决该问题。
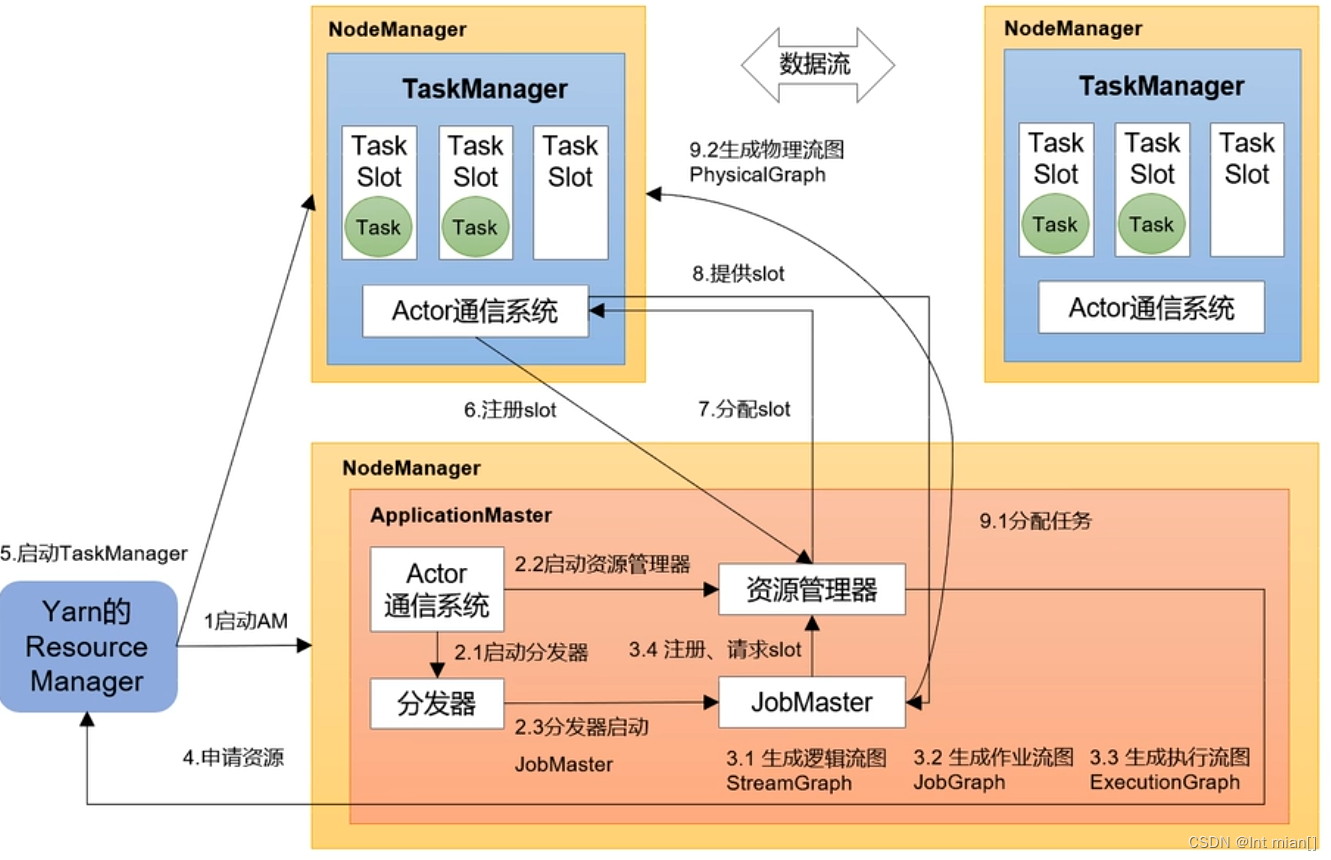
Swin Transformer 的网络结构
其中Swin Transformer的结构采用层级化设计,一共分为4个阶段。
设将一个图像 ( H , W , 3 ) (H,W,3) (H,W,3)输入到Patch Partition模块中进行分块,设每一个Patch为 4 × 4 4\times4 4×4的大小,则每一个Path的大小为16个像素,所以可以将一个大小为 ( H , W , 3 ) (H,W,3) (H,W,3)大小的图像转换为 ( H 4 , H 4 , 4 × 4 × 3 ) (\frac{H}{4},\frac{H}{4},4\times4\times3) (4H,4H,4×4×3),然后通过Linear Embeding层将一个 ( H 4 , H 4 , 48 ) (\frac{H}{4},\frac{H}{4},48) (4H,4H,48)的向量大小的Patch转化为 ( H 4 , H 4 , C ) (\frac{H}{4},\frac{H}{4},C) (4H,4H,C)的大小,其中Patch Partition和Linear Embeding可以直接通过一个卷积层实现的。也就是说以图像大小224×224×3为例,经过第一层后数据维度变为56×56×(4×4×3), 之后送入阶段1进行处理。
然后通过四个Stage构建不同大小的特征图,除了Stage1中先通过一个Linear Embeding层外,剩下三个stage都是先通过一个Patch Merging层进行下采样。
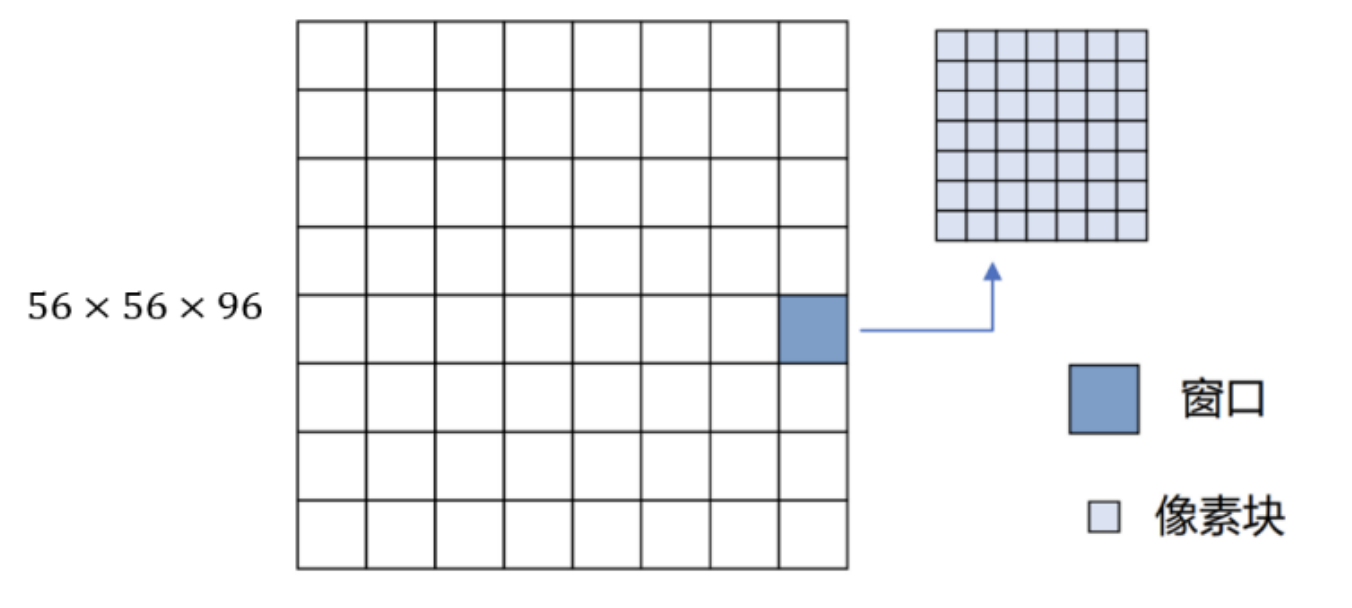
其中Swin Transformer采用了窗口内自注意力(W-MSA),在阶段1中,数据从线性嵌入层出来之后,维度大小变为3136×96,这对于 Transformer块来说过大,因此需采用窗口内自注意力计算减小计算复杂度。
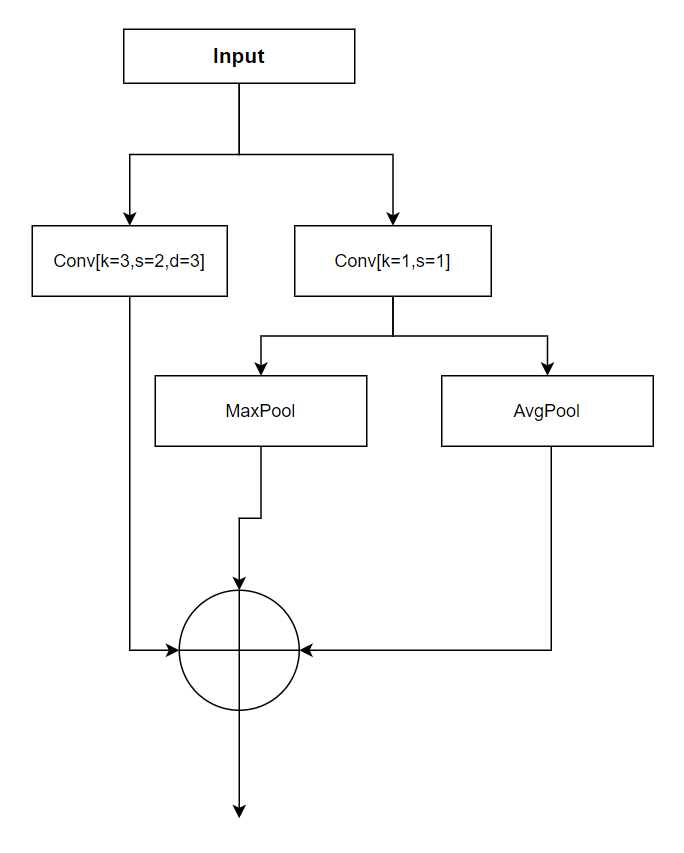
其中Swin-T block的结构如图所示
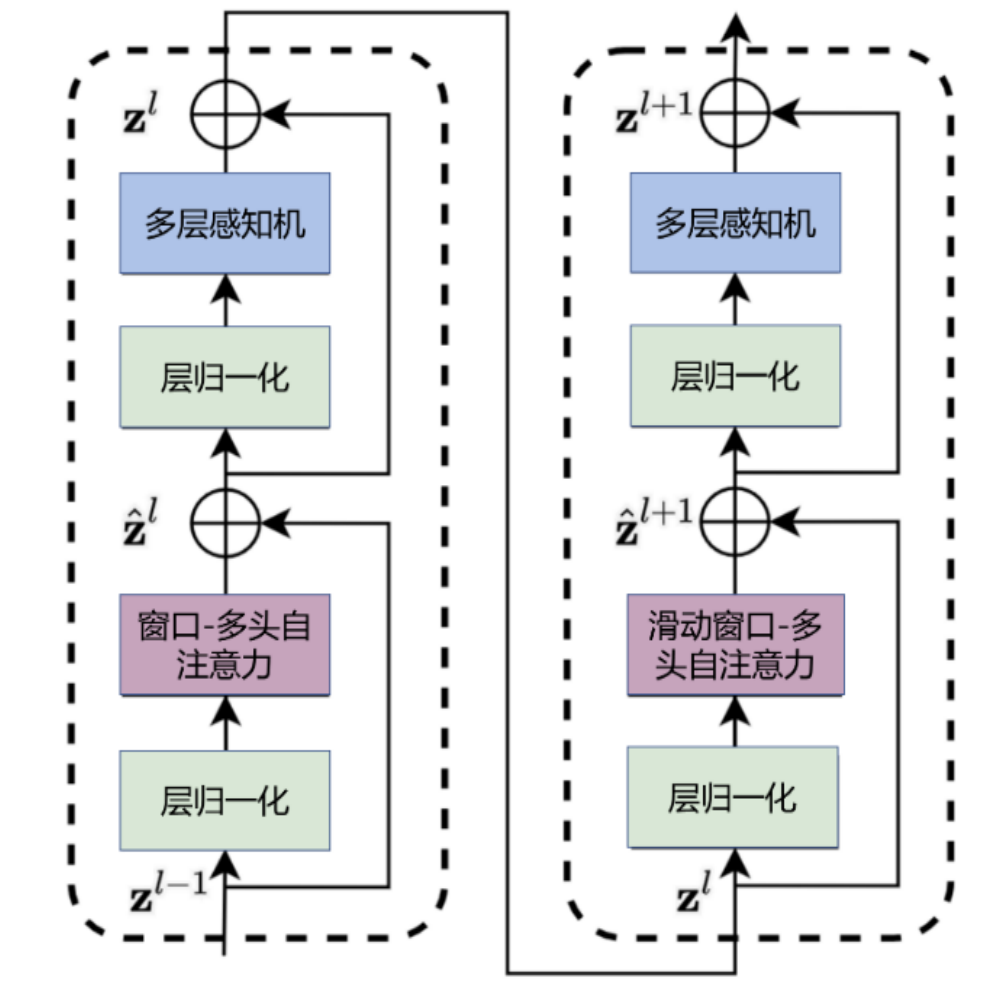
W-MSA 窗口多头注意力机制
Swin-T将特征图划分为多个窗口,然后对每一个窗口进行自注意力的计算,这可以有效的的减少计算量。
具体来说,自注意力计算流程如下图所示。向量与三个系数矩阵相乘后分别得到Q、K和V。然后Q与K相乘得到自注意力A,A再与V相乘,然 后经过投射层得到最终结果。
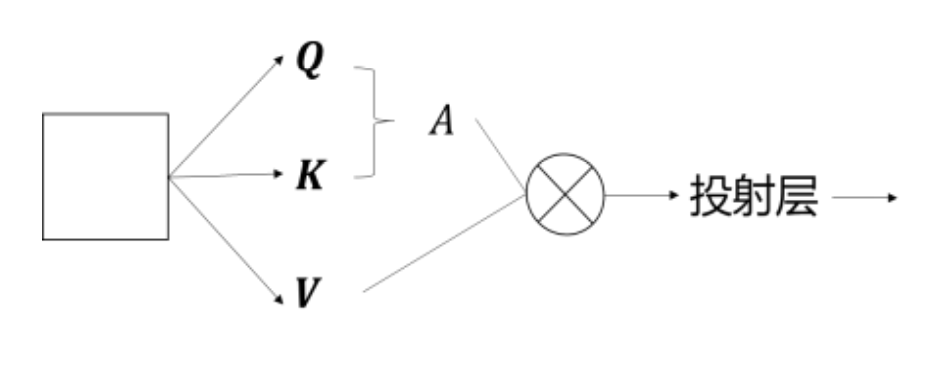
普通的自注意力计算复杂度为 Ω ( M S A ) = 4 h w C 2 + 2 ( h w ) 2 C \Omega(MSA)=4hwC^2+2(hw)^2C Ω(MSA)=4hwC2+2(hw)2C,而窗口内自注意力计算复杂度为 Ω ( W − M S A ) = 4 h w C 2 + 2 M 2 C \Omega(W-MSA)=4hwC^2+2M^2C Ω(W−MSA)=4hwC2+2M2C。
SW-MSA 滑动窗口多头注意力机制
Swin Transformer使用窗口内自注意力计算,虽然可以大大减小计算复杂度,但是也让不同像素块缺少与其他像素块之间的联系。为了增加感受野,变相达到全局建模的能力,于是作者提出了滑动窗口机制。
如下图所示,红色正方形围住的部分是窗口,每个窗口内灰色的正方形为像素块。每次滑动时,窗口都向右下方向移动2个像素块。于是Layer l+1的第2个窗口(从1开始计算)综合了layer l的第1个和第2个窗口的信息,Layer l+1的第5个窗口(从1开始计算)综合了layer l的所有窗口的信息,所以可以综合获得全局信息。
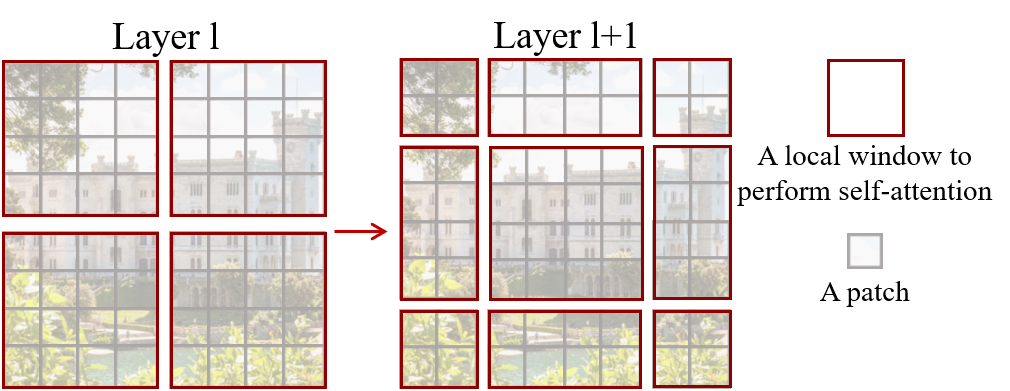
如图所示设窗口大小为 4 × 4 4\times4 4×4。窗口的移动步长为 2 × 2 2\times2 2×2左上角从第0行第0列移动到第2行第2列由此产生了9个大小不一致的窗口,为了降低计算了,作者通过移动窗口的方式重新和合并成4个 4 × 4 4\times4 4×4的窗口。如下图所示。
但是在这样得到的新窗口内可能存在两个本来相距很远的像素块,它们本 来不应该放在一起计算,因此使用掩码多头自注意力解决,通过设置蒙板来隔绝不同区域的信息。在计算完毕后,再将其复原,否则该图就不断往右下方向循环下去了。
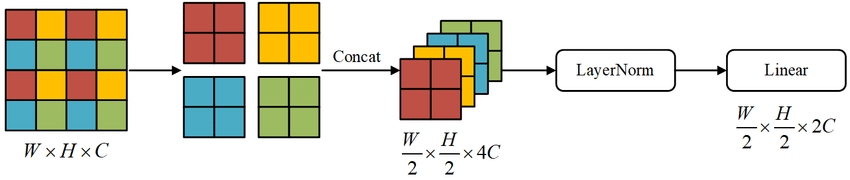
Patch Merging 图块合并
从阶段2开始,之后的每一阶段都是一个像素块合并层和Swin Transforme块,其中像素块合并层类似于卷积神经网络中的池化层,经过像素块合并层之后,数据的宽和高为原先的1/2,通道数为原先的2倍。