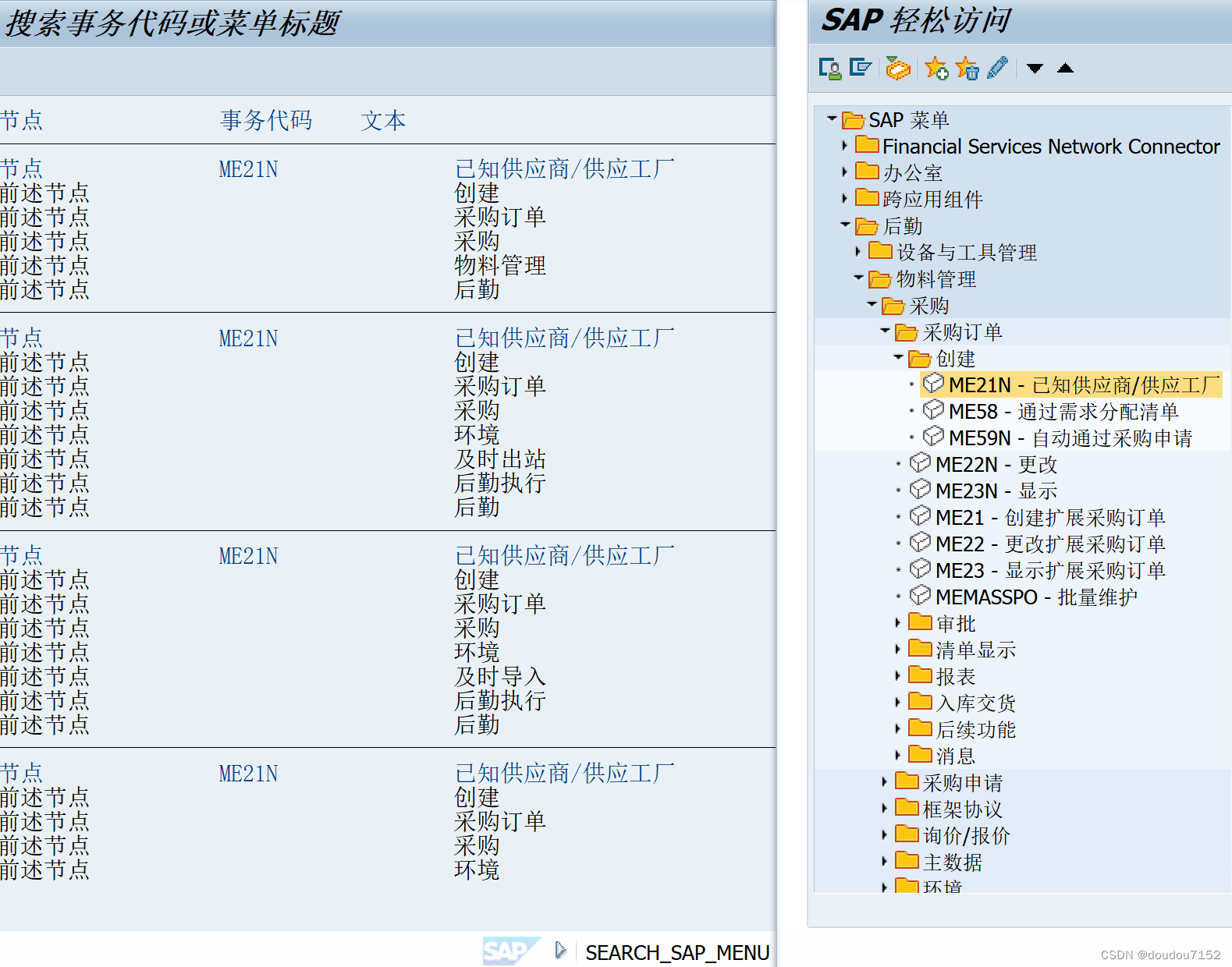
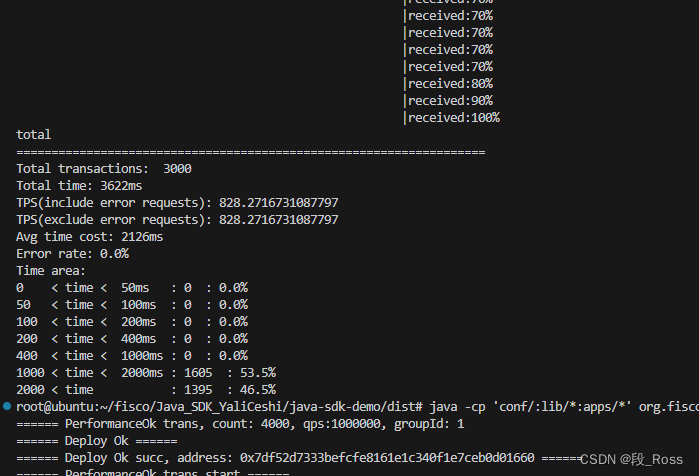
p17

1，

个人解答：

int DeleteMinElem(SqList &L,int &min)
{
	int j = 0;
	if (L.length == 0)
	{
		printf("error!");
		return 0;
	}
	int min = L.data[0];
	for (int i = 1; i < L.length; i++)
	{
		if (L.data[i] < min)
		{
			min = L.data[i];
			j = i;
		}
	}
	L.data[j] == L.data[L.length - 1];//原本的位置换成最后一个元素
	L.length--;
	return min;
}

问题：一般采用布尔类型判断是否执行成功，同时利用&引用不需要再返回最小值

bool DeleteMinElem(SqList &L,int &min)
{
	int j = 0;
	if (L.length == 0)
	{
		return false;
	}
	int min = L.data[0];
	for (int i = 1; i < L.length; i++)
	{
		if (L.data[i] < min)
		{
			min = L.data[i];
			j = i;
		}
	}
	L.data[j] == L.data[L.length - 1];//原本的位置换成最后一个元素
	L.length--;
	return true;
}

2，元素逆置，时间复杂度要求O（1）

思路：顺序表长度确定：

void Reverse(SqList& L)
{
	int temp = 0;
	for (int i=0; i < L.length/2; i++)//前后半段对应元素交换
	{
		temp = L.data[i];
		L.data[i] = L.data[L.length - 1 - i];
		L.data[L.length - 1 - i] = temp;

	}
}

3，删除所有值为x的元素

思路：每次删除都将后面的数字向前移动更新占用的时间复杂度和空间复杂度都较高，采用新的下标记录值不为x的元素作为L的新数组

void DeleteX(SqList& L, int x)
{
	int k = 0;
	for (int i = 0; i < L.length; i++)
	{
		if (L.data[i] != x)
			L.data[k++] = L.data[i];//用k来对data数组进行更新
	}
	L.length = k;
}

4，删除s和t之间的元素

个人代码：

bool DeleteStoT(SqList& L,int s,int t)//s和t是值，不是下标
{
	int k = 0; //记录两元素的下标
	if (L.length == 0||s>=t)
		return false;
	for (int i = 0; i < L.length; i++)
	{
		if (L.data[i] <= s || L.data[i] >= t)
			L.data[k++] = L.data[i];
	}

	L.length = k;
	return true;
}

为什么不使用k?因为顺序表不能为空，如果使用k的情况下顺序表中没有符合的元素就为空表，而本题中没有符合发元素则返回false

思路：有序表那么删除的元素是连通的，先找到大于s的第一个元素（第一个删除的元素），然后寻找大于t的第一个元素（最后一个删除的元素的下一个元素），然后将后面的元素前移，

不包含st是指结果中没有st

bool Del_s_t2(SqList &L,int s,int t)
{
int i,j;
if(s>=t||L.length==0)
return false;
for(i=0;i<L.length&&L.data[i]<=s;i++);//寻找大于s的第一个元素
if(i>=L.length)
return false;//结果为空表的情况返回错误
foe(j=i;j<L.length&&L.dada[j]<=t;j++);//寻找大于t的第一个元素
for(;j<L.length;i++,j++)
L.data[i]=L.data[j];//数据前移
L.length=i;//更新长度
return true;
}

5，包含st是指删除的数字包含st

可以使用k记录需要删除的元素的数量

bool DeleteStoT2(SqList& L, int s, int t)//s和t是值，不是下标
{
	int k = 0; //记录两元素的下标
	if (L.length == 0 || s >= t)
		return false;
	for (int i = 0; i < L.length; i++)
	{
		if (L.data[i] >= s && L.data[i] <= t)
			k++;
		else
			L.data[i - k] = L.data[i];

	}

	L.length -= k;
	return true;
}

6,删除重复的值

思路：一个变量用来存储新的顺序，一个变量用来遍历，如果遍历到的数字与上一个存储的数字不同，则放入新的顺序表中

bool DeleteSame(SqList& L)//s和t是值，不是下标
{
	int i, j = 0;
	if (L.length == 0 )
		return false;
	for (i = 0,j=1; j < L.length; j++)
	{
		if (L.data[i] != L.data[j])
			L.data[++i] = L.data[j];//下标加1，所以是++i而不是i++
	}

	L.length=i+1;
	return true;
}

7，设计思路：

用三个不同的变量记录每个链表遍历到的结点，i,j往下一个遍历的条件是前一个结点已经被记录到新数组中，注意：两链表的长度和不可以超出新链表的长度，当一个链表已经遍历完成，后一个表可以直接挪到新链表中

bool Combine(SqList L1, SqList L2, SqList L)
{
	int i, j, k = 0;
	if (L1.length + L2.length > MaxSize) {//超出最大容量
		return false;
	}
	while (i < L.length && j < L.length)
	{
		if (L1.data[i] <= L2.data[j])//两链表中出现同样的数字也放入新链表中，所以此处并不冲突
			L.data[k++] = L1.data[i++];
		else
			L.data[k++] = L1.data[j++];
	}
	while(i<L.length)
		L.data[k++] = L1.data[i++];
	while (j<L.length)
		L.data[k++] = L1.data[j++];
	L.length = k;
	return true;

}

8，思路：先将数组中m+n个数字全部转置，然后1-m个数字，m+1-m+n个数字再分别转置