5 洛必达法则

极限的种类

令$N$为常数，则常规的极限运算大致有以下几种

$$\begin{array}{cccc}& \infty \pm N=\infty & \infty \divideontimes N=\infty (N\ne 0)& N\dotplus \infty =\infty \\ & N-\infty =-\infty & N/\infty =0& \pm N/0=\pm \infty \\ & N^{\infty }=\infty (N\ne 1)& {\infty }^N=\infty (N\ne 0)& \end{array}$$

常规之外，就要通过洛必达法则来处理

$$\frac{0}{0},\frac{\infty }{\infty },0\cdot \infty ,\infty -\infty ,0^0,{\infty }^0,1^{\infty }$$

对于$\frac{0}{0},\frac{\infty }{\infty }$而言，洛必达法则在形式上可以表示为

$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$$

洛必达法则作用于幂函数

理解洛必达法则可从幂函数入手，假设$f(x)=x^n$，$g(x)=x^m$，则$\frac{f(x)}{g(x)}=x^{n-m}$。当$x\to 0$时，若$n-m>0$，则极限为无穷大，否则极限为0。

所以，尽管二者都为0，但0和0也有不同。问题是这种不同是否明显？如果定义域在$[-1,1]$这个区间，的确看不出太多的区别

x = seq(-1,1,0.01)  #生成等差数列
plot(x,x^2,type='l')
lines(x,x^3)
lines(x,x^4)
lines(x,x^5)
lines(x,x^6)

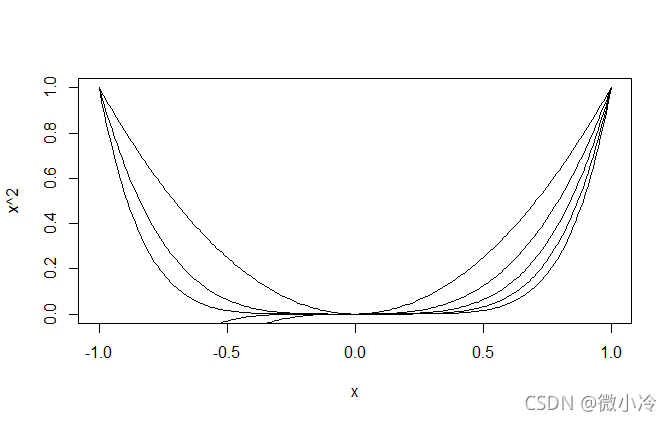
然而随着我们缩小坐标的尺度，区别就变得明显起来

> x = seq(-0.1,0.1,0.001)
> plot(x,x^2,type='l')
> lines(x,x^3)

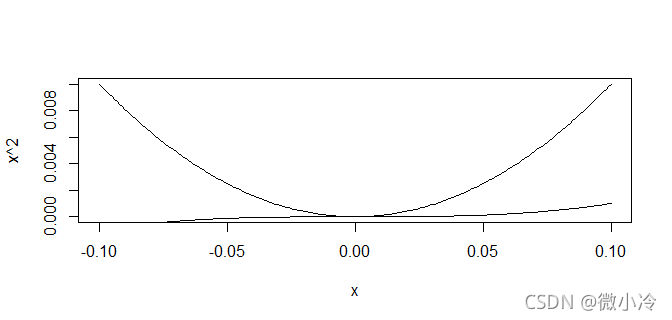
这意味着越是逼近0，不同阶数的幂函数将渐行渐远，回顾极限的定义，对于

$$\underset{x\to 0}{\lim }\frac{x^3}{x^2}=0$$

意味着对于任意小的$\epsilon$，均能找到一个$X$，当$x\in [0,X]$时，有$\frac{x^3}{x^2}<\epsilon$，这是显然的。

而我们之所以觉得“显然”，是因为我们接受了大量的指数运算的训练，而指数之间的运算又基于一条更简单的规则$\frac{x^n}{x}=x^{n-1}$。或许其真正的运算过程为

$$\frac{x^3}{x^2}=\frac{\frac{x^3}{x}}{\frac{x^2}{x}}=\frac{x^2}{x}=x$$

受到这种运算形式的启发，对于一个相对复杂的表达式，或许可以对上式进行一点更改

$$\underset{x\to 0}{\lim }\frac{f(x)}{g(x)}=\underset{x\to 0}{\lim }\frac{\frac{f(x)-0}{x}}{\frac{g(x)-0}{x}}=0$$

这个时候我们就发现了一个很熟悉的表达式${\lim }_{x\to 0}\frac{f(x)-0}{x}$，正是

$$f^{\prime }(0)=\underset{x\to 0}{\lim }\frac{f(0+x)-f(0)}{x}$$

所以，对于$f(0)=0$和$g(0)=0$的情况，可以存在

$$\underset{x\to 0}{\lim }\frac{f(x)}{g(x)}=\frac{f^{\prime }(0)}{g^{\prime }(0)}$$

若$f^{\prime }(0)$和$g^{\prime }(0)$仍然同时为0，则继续洛，一直洛到祖坟上去。回顾一开始引入的重要极限，洛必达法则很好地验证了其正确性。

$$\underset{x\to 0}{\lim }\frac{\sin (x)}{x}=\underset{x\to 0}{\lim }\frac{{\sin }^{\prime }x}{x^{\prime }}=\frac{\cos 0}{1}=1$$

可以画图验证一下二者在趋近于0时的特性

x = seq(-0.01,0.01,0.001)
plot(x,x,ylab="x/sin(x)")
lines(x,sin(x),col='red')

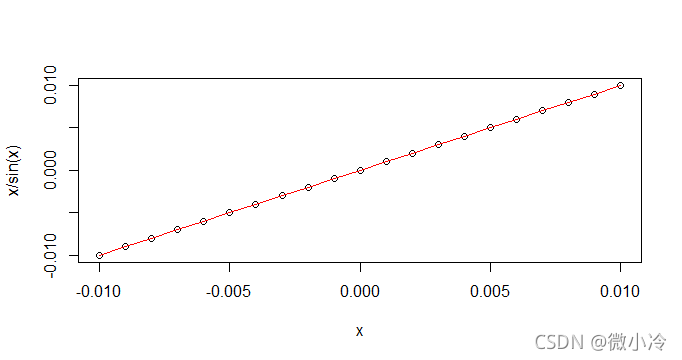
由于实在靠的太近，所以用差的对数来表示一下

x = seq(-0.1,0.1,0.001)
err = log(abs(x-sin(x)),10)
plot(x,err,type='l')

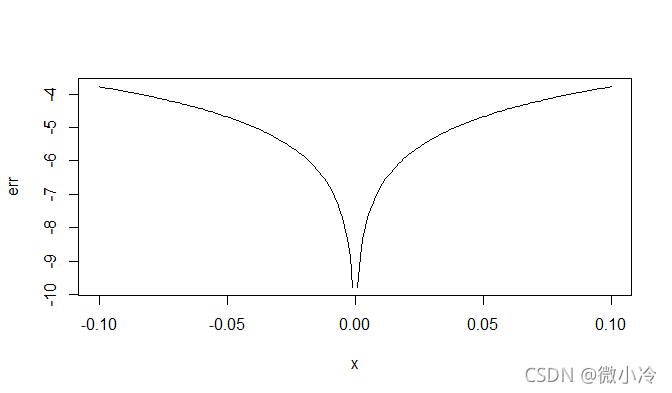
可见这个收敛速度是很快的，当$x=0.001$时，二者之间的差就已经达到了$10^{-9}$。