高级树结构之平衡二叉树（ALV树）

news2024/11/17 13:43:53

文章目录

  • 平衡二叉树简介
  • 失衡类型&处理办法
    • RR型失衡【左旋调整】
      • 调整演示
      • 代码实现
    • LL型失衡【右旋调整】
      • 调整演示
      • 代码实现
    • RL型失衡【先右旋后左旋调整】
      • 调整演示
      • 代码实现
    • LR型失衡【先右旋后左旋调整】
      • 调整演示
      • 代码实现
    • 插入操作
    • 综合代码演示

平衡二叉树简介

  • 在数据有序的情况下，进行动态二叉树的创建时，二叉树会变得非常长。那么在进行查找某个节点的时候，就会变成线性查找。
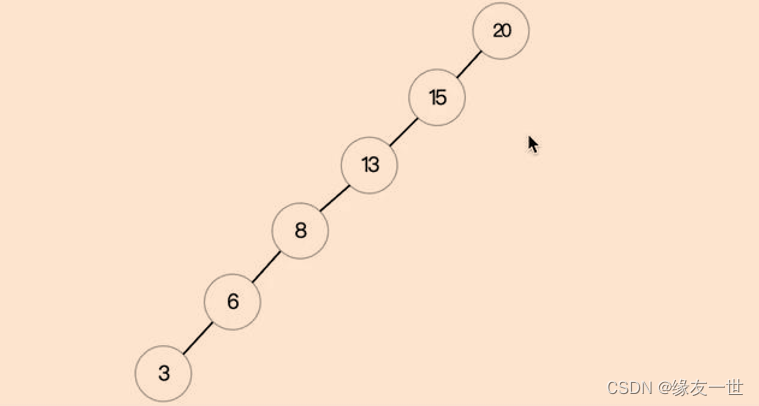
    在这里插入图片描述
  • 平衡二叉树：一颗左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树的二叉排序树。
    • 注意：空树也是一颗平衡二叉树
  • 平衡二叉树的性质：
    • 平衡二叉树是一颗二叉查找树
    • 任意节点的左右子树也是一颗平衡二叉树
    • 从根节点开始，左右子树的高度差不超过1，否则视为不平衡
  • 平衡因子：二叉树上结点的左子树的高度减去右子树高度得到的结果为该节点的平衡因子
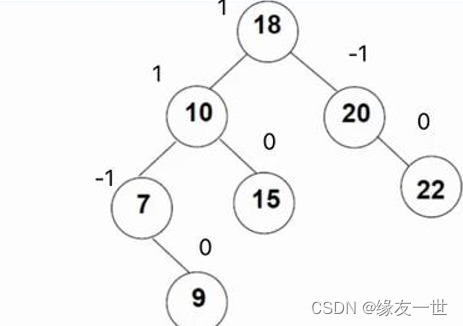
    在这里插入图片描述
  • 通过平衡因子的计算，可以判断二叉树是否失衡
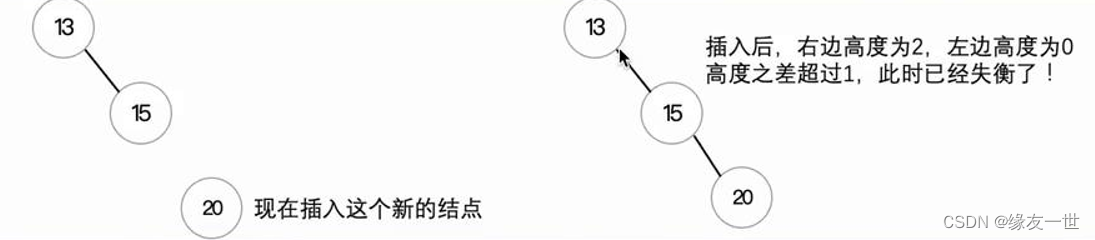
    在这里插入图片描述
  • 为此，我们需要对失衡的二叉树进行调整使其保持平衡

失衡类型&处理办法

  • 为了保证二叉树的平衡，需要将其进行旋转来维持平衡，去纠正最小不平衡子树即可

RR型失衡【左旋调整】

  • RR型最小不平衡子树模型
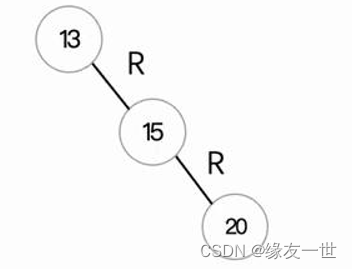
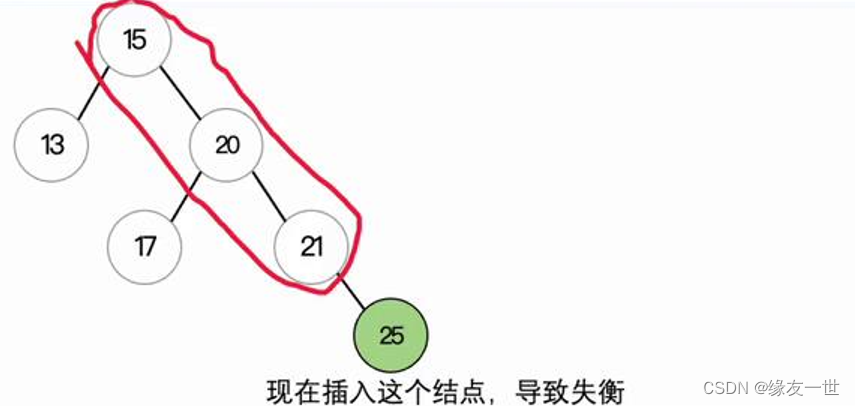
    在这里插入图片描述
    在这里插入图片描述

调整演示

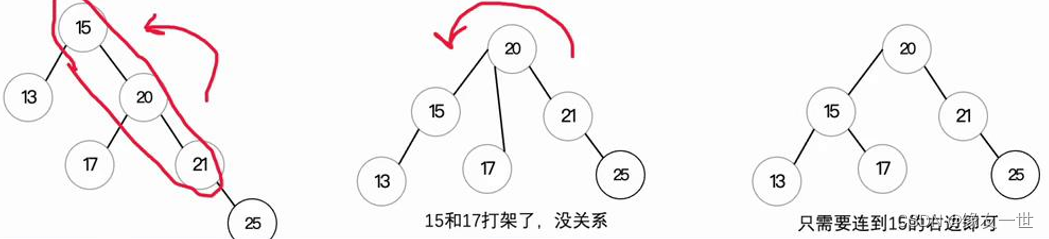
  • 从根节点开始向右的三个结点进行左旋操作。左旋操作要将这三个结点中间的结点作为新的根节点，其他两个结点变为左右子树
    在这里插入图片描述

代码实现

int max(int a,int b) {
    return a>b ? a:b;
}

int getHeight(Node root) {
    if(root==NULL) return 0;
    return root->height;
}

//RR调整:左旋转
Node leftRotation(Node root) {
    Node newNode=root->right;
    root->right=newNode->left;
    newNode->left=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

LL型失衡【右旋调整】

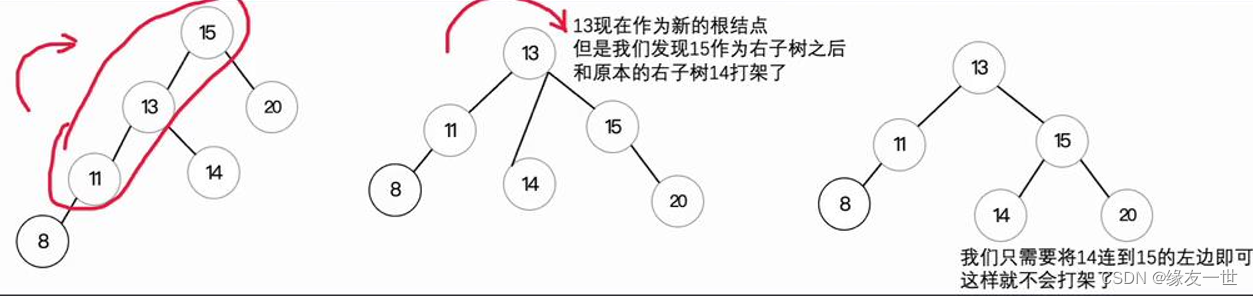
  • LL型最小不平衡子树模型
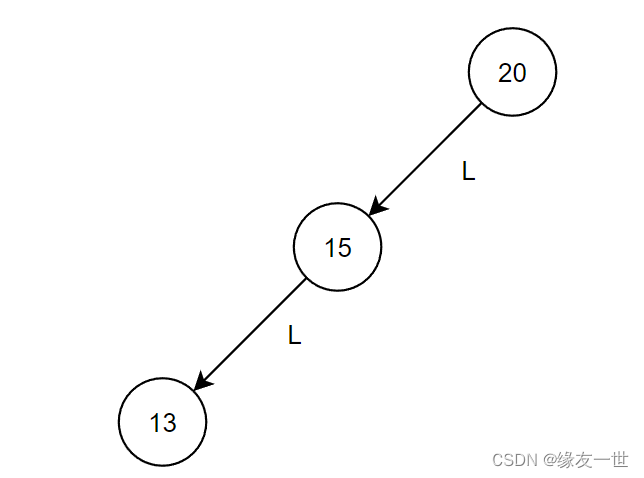
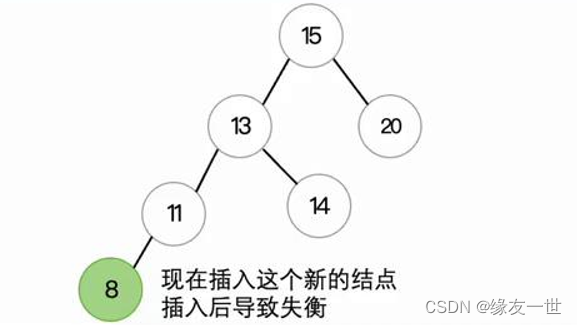
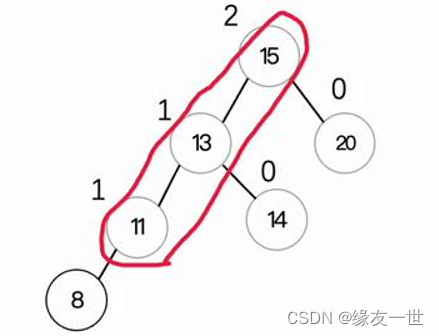
    在这里插入图片描述

在这里插入图片描述

  • 通过计算平衡因子，找到最小不平衡子树
    在这里插入图片描述

调整演示

  • 从根节点开始向左的三个结点进行右旋操作。右旋操作要将这三个结点中间的结点作为新的根节点，其他两个结点变为左右子树
    在这里插入图片描述

代码实现

int max(int a,int b) {
    return a>b ? a:b;
}

int getHeight(Node root) {
    if(root==NULL) return 0;
    return root->height;
}

//LL调整:右旋转
Node rightRotation(Node root) {
    Node newNode=root->left;
    root->left=newNode->right;
    newNode->right=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

RL型失衡【先右旋后左旋调整】

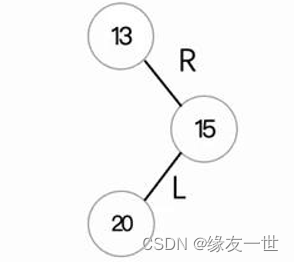
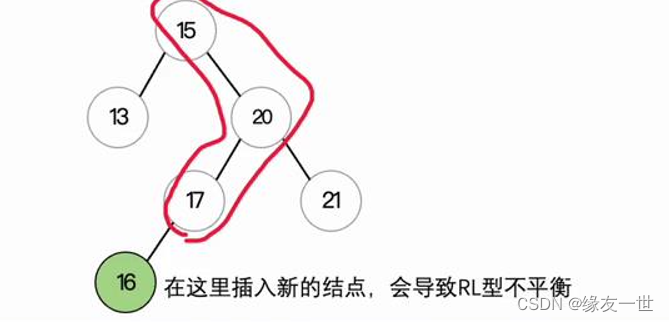
  • RL型最小不平衡子树模型
    在这里插入图片描述
    在这里插入图片描述

调整演示

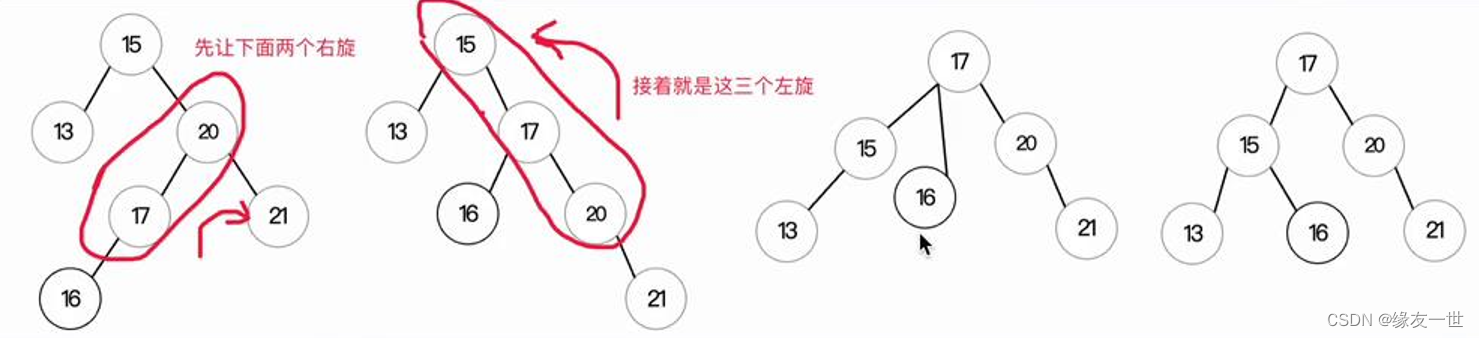
  • 对于先右边后左边的情况，需要先右旋后左旋
  • 注意：右旋操作针对两个结点
    在这里插入图片描述

代码实现

int max(int a,int b) {
    return a>b ? a:b;
}

int getHeight(Node root) {
    if(root==NULL) return 0;
    return root->height;
}

//RR调整:左旋转
Node leftRotation(Node root) {
    Node newNode=root->right;
    root->right=newNode->left;
    newNode->left=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

//LL调整:右旋转
Node rightRotation(Node root) {
    Node newNode=root->left;
    root->left=newNode->right;
    newNode->right=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}


//RL调整:先右旋，后左旋
Node rightLeftRotation(Node root) {
    //注意这里如果newNode的right指向可以为空，符合案例的要求
    root->right= rightRotation(root->left);
    //然后左旋并返回根节点
    return leftRotation(root);
}

LR型失衡【先右旋后左旋调整】

  • LR型最小不平衡子树模型
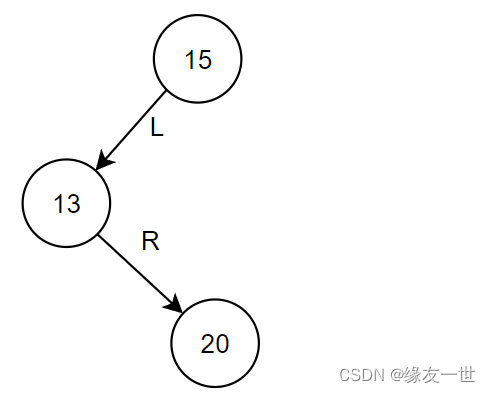
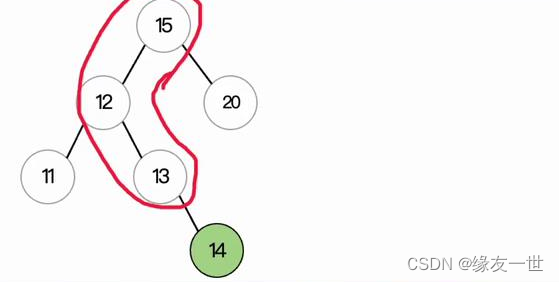
    在这里插入图片描述
    在这里插入图片描述

调整演示

  • 先左旋，后优旋
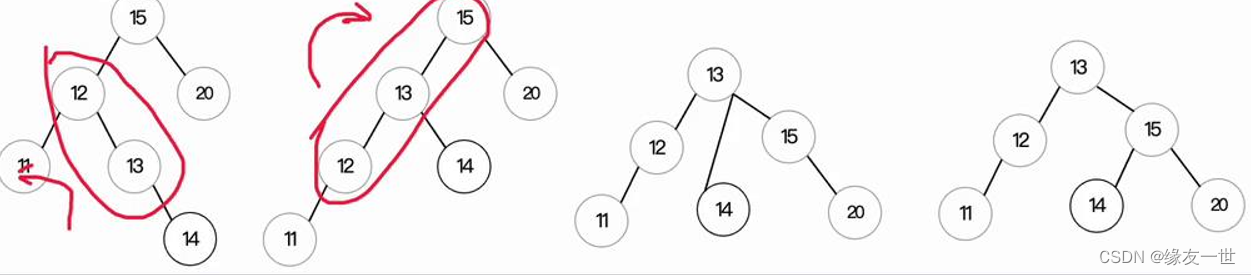
    在这里插入图片描述

代码实现

int max(int a,int b) {
    return a>b ? a:b;
}

int getHeight(Node root) {
    if(root==NULL) return 0;
    return root->height;
}

//RR调整:左旋转
Node leftRotation(Node root) {
    Node newNode=root->right;
    root->right=newNode->left;
    newNode->left=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

//LL调整:右旋转
Node rightRotation(Node root) {
    Node newNode=root->left;
    root->left=newNode->right;
    newNode->right=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

//LR调整:先左旋，后右旋
Node leftRightRotation(Node root) {
    //注意这里如果newNode的left指向可以为空，符合案例的要求
    root->left= leftRotation(root->left);
    //然后右旋并返回根节点
    return rightRotation(root);
}

插入操作

  • 插入结点时要注意维护整棵树的平衡因子保证其处于稳定状态，防止其退化。
  • 插入结点的思路大体上与创建二叉排序数类似
  • 同时要注意时刻保持数的平衡性。最后在查入完成后，记得及时更新节点的高度
Node insert(Node root,E element) {
    //如果结点为NULL，说明找到了插入的位置
    //小于相对根节点的往左边放
    //大于相对根节点的往右边放
    if(root == NULL) {
        root= createNode(element);
    }else if(element < root->element) {
        root->left= insert(root->left,element);
        //插入完成之后，计算平衡因子 判断是否失衡 并进行相关的调整
        if(getHeight(root->left) - getHeight(root->right)> 1) {
            //然后判断插入的数值在左子树的右边还是左边，如果在左边就是LL调整【右旋】否则就是LR调整【先左旋，后右旋】
            if(element < root->left->element) {
                root= rightRotation(root);//LL型右旋之后，得到新的根节点
            }else {
                root= leftRightRotation(root);//LR型 先左旋后右旋，得到新的根节点
            }
        }
    }else if(element > root->element) {
        root->right= insert(root->right,element);
        //插入完成之后，计算平衡因子 判断是否失衡 并进行相关的调整
        if(getHeight(root->left) - getHeight(root->right) < -1) {
            //然后判断插入的数值在右子树的右边还是左边，如果在右边就是RR调整【左旋】否则就是RL调整【先右旋，后左旋】
            if(element > root->right->element)
                root= leftRotation(root);//RR型左旋之后，得到新的根节点
            else
                root= rightLeftRotation(root);//RL型 先右旋后左旋，得到新的根节点
        }

    }
    //最后更新最新的结点的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    //最后返回root到上一级
    return root;
}

综合代码演示

  • 这里将之前各个部分的档案码全部展示出来，有不明白的可以直接粘贴复制进行调试探究
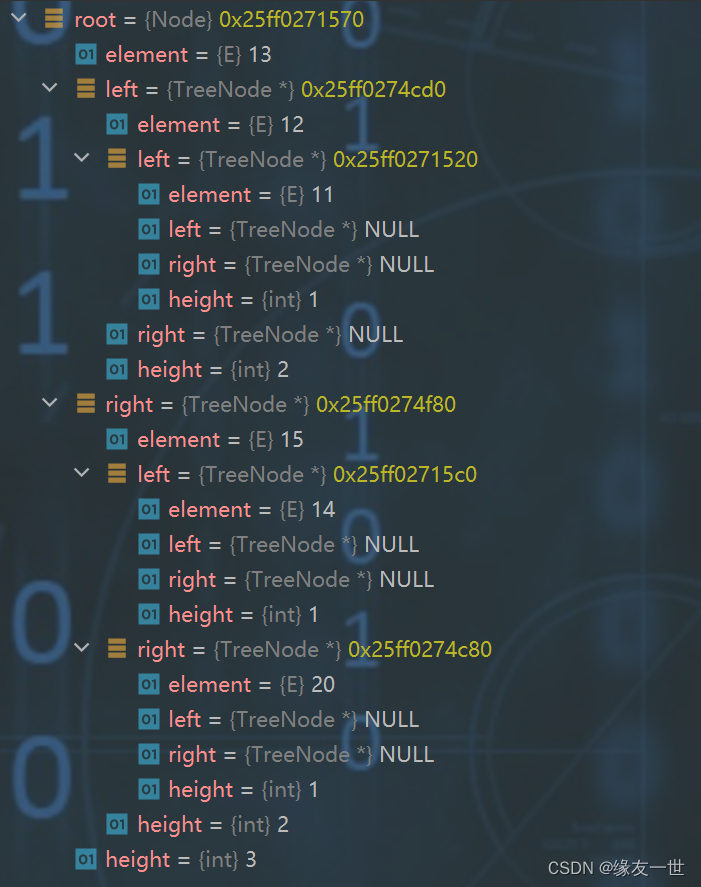
  • 演示二叉树的结构
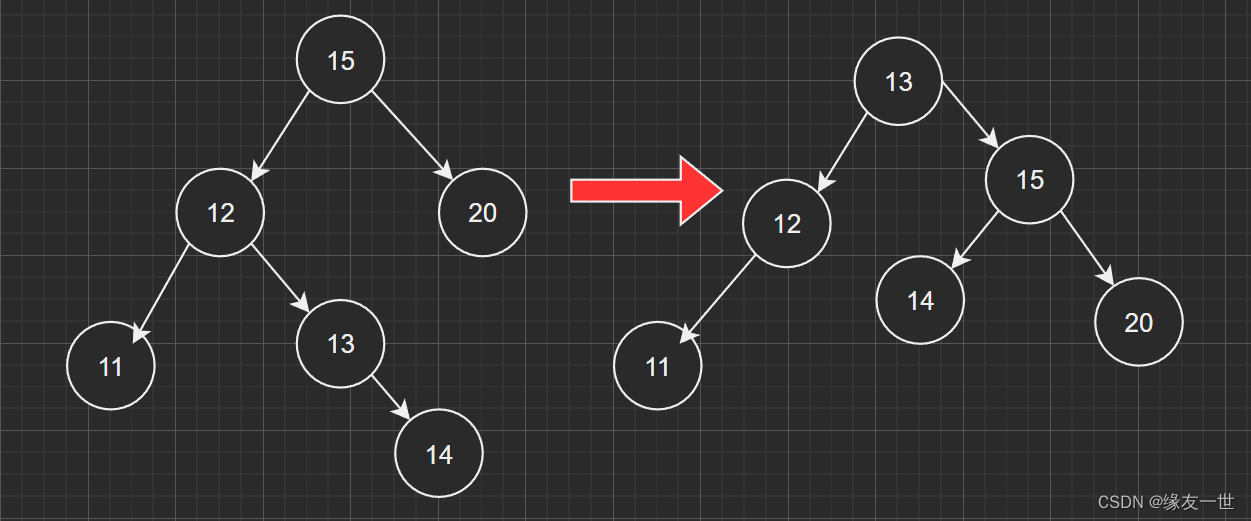
    在这里插入图片描述
#include<iostream>
using namespace std;
typedef int E;
typedef struct TreeNode{
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    //每个结点需要记录当前子树的高度，便于计算平衡因子
    int height;
}* Node;

Node createNode(E element) {
    Node node=(Node)malloc(sizeof(struct TreeNode));
    node->left=node->right=NULL;
    node->element=element;
    node->height=1;//树的初始化高度为1
    return node;
}

int max(int a,int b) {
    return a>b ? a:b;
}

int getHeight(Node root) {
    if(root==NULL) return 0;
    return root->height;
}

//RR调整:左旋转
Node leftRotation(Node root) {
    Node newNode=root->right;
    root->right=newNode->left;
    newNode->left=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

//LL调整:右旋转
Node rightRotation(Node root) {
    Node newNode=root->left;
    root->left=newNode->right;
    newNode->right=root;
    //计算结点高度的时候，不要忘记算上自身的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    newNode->height=max(getHeight(newNode->left), getHeight(newNode->right))+1;
    return newNode;
}

//LR调整:先左旋，后右旋
Node leftRightRotation(Node root) {
    //注意这里如果newNode的left指向可以为空，符合案例的要求
    root->left= leftRotation(root->left);
    //然后右旋并返回根节点
    return rightRotation(root);
}

//RL调整:先右旋，后左旋
Node rightLeftRotation(Node root) {
    //注意这里如果newNode的right指向可以为空，符合案例的要求
    root->right= rightRotation(root->left);
    //然后左旋并返回根节点
    return leftRotation(root);
}

Node insert(Node root,E element) {
    //如果结点为NULL，说明找到了插入的位置
    //小于相对根节点的往左边放
    //大于相对根节点的往右边放
    if(root == NULL) {
        root= createNode(element);
    }else if(element < root->element) {
        root->left= insert(root->left,element);
        //插入完成之后，计算平衡因子 判断是否失衡 并进行相关的调整
        if(getHeight(root->left) - getHeight(root->right)> 1) {
            //然后判断插入的数值在左子树的右边还是左边，如果在左边就是LL调整【右旋】否则就是LR调整【先左旋，后右旋】
            if(element < root->left->element) {
                root= rightRotation(root);//LL型右旋之后，得到新的根节点
            }else {
                root= leftRightRotation(root);//LR型 先左旋后右旋，得到新的根节点
            }
        }
    }else if(element > root->element) {
        root->right= insert(root->right,element);
        //插入完成之后，计算平衡因子 判断是否失衡 并进行相关的调整
        if(getHeight(root->left) - getHeight(root->right) < -1) {
            //然后判断插入的数值在右子树的右边还是左边，如果在右边就是RR调整【左旋】否则就是RL调整【先右旋，后左旋】
            if(element > root->right->element)
                root= leftRotation(root);//RR型左旋之后，得到新的根节点
            else
                root= rightLeftRotation(root);//RL型 先右旋后左旋，得到新的根节点
        }

    }
    //最后更新最新的结点的高度
    root->height=max(getHeight(root->left), getHeight(root->right))+1;
    //最后返回root到上一级
    return root;
}

void inOrder(Node root) {
    if(root==NULL) return ;
    inOrder(root->left);
    cout<<root->element<<" ";
    inOrder(root->right);
}

int main() {
    Node root=NULL;
    root= insert(root,15);
    root= insert(root,20);
    root= insert(root,12);
    root= insert(root,11);
    root= insert(root,13);
    root= insert(root,14);
    inOrder(root);
    return 0;
}

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/160391.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Codeforces Round #842 (Div. 2)

Codeforces Round #842 (Div. 2)

Codeforces Round #843 (Div. 2) 传送门 不想搞的很累&#xff0c;对自己不做要求&#xff0c;有兴趣就做。 A. Greatest Convex #include <bits/stdc.h>using namespace std; const int maxn 1e6 10; vector<int> cnt[maxn]; map<int, int> mp;int mai…
阅读更多...
nvm安装 疑难问题解决

nvm安装 疑难问题解决

nvm介绍 NVM是node.js的版本管理器&#xff0c;设计为每个用户安装&#xff0c;并在每个shell中调用。nvm可以在任何兼容posix的shell (sh、dash、ksh、zsh、bash)上运行&#xff0c;特别是在这些平台上:unix、macOS和windows WSL。 nvm安装 &#xff01;&#xff01;重要&a…
阅读更多...
强化学习在智能补货场景的应用

强化学习在智能补货场景的应用

本文作者&#xff1a;应如是&#xff0c;观远算法团队工程师&#xff0c;毕业于伦敦帝国理工学院计算机系&#xff0c;主要研究方向为强化学习、时间序列算法及其落地应用。深耕零售消费品场景&#xff0c;解决供应链运筹优化问题。为客户提供基于机器学习的AI解决方案。1. 背景…
阅读更多...
2023.Q1 go语言记录

2023.Q1 go语言记录

1. Go 语言数组声明和初始化var variable_name [SIZE] variable_type&#xff0c;eg&#xff1a;var balance [10] float32var balance [5]float32{1000.0, 2.0, 3.4, 7.0, 50.0}balance : [5]float32{1000.0, 2.0, 3.4, 7.0, 50.0}长度不确定的初始化var balance [...]float…
阅读更多...
少儿Python每日一题（21）：八皇后问题

少儿Python每日一题（21）：八皇后问题

原题解答 本次的题目如下所示： 会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 8个方格），使它们谁也不能被吃掉！这就是著名的八皇后问题。 对于某个满足要求的8皇后的摆放方法，定义一个皇后串a与之对应，即，…
阅读更多...
【Ansible】Ansible Playbook 的任务控制

【Ansible】Ansible Playbook 的任务控制

Ansible Playbook 的任务控制 文章目录Ansible Playbook 的任务控制一、Ansible 任务控制基本介绍二、条件判断1.解决第一个问题2.nginx 语法校验三、循环控制四、Tags 属性五、Handlers 属性一、Ansible 任务控制基本介绍 任务控制类似于编程语言中的 if …、for …等逻辑控制…
阅读更多...
MSF社会工程学

MSF社会工程学

● Metasploit发现两个远程代码执行漏洞 ○ 问题都出在WEB组件方面 ○ MSF不受影响 ● 安全面前任何软件都是平等的 ○ 没有绝对安全的软件 为什么要说社会工程学 ● Metasploit可以很好的配合到社会工程学攻击的各个阶段 ● Setoolkit工具包大量依赖Metasploit ● 基于浏览器…
阅读更多...
[SUCTF 2019]EasySQL

[SUCTF 2019]EasySQL

目录 预先知识 信息收集 思路 源码分析 非预期解 预期解 补充 预先知识 环境 use mysql; create table if not exists my_table( id int PRIMARY key auto_increment, name VARCHAR(20), age int); insert into my_table values(NULL,xiao,19); insert into my_table v…
阅读更多...
BUFF80双模蓝牙5.2热插拔PCB

BUFF80双模蓝牙5.2热插拔PCB

键盘使用说明索引&#xff08;均为出厂默认值&#xff09;软件支持一些常见问题解答&#xff08;FAQ&#xff09;首次使用测试步骤蓝牙配对规则&#xff08;重要&#xff09;蓝牙和USB切换键盘默认层默认触发层0的FN键配置的功能默认功能层1配置的功能默认的快捷键蓝牙参数蓝牙…
阅读更多...
Jetpack Compose中的Canvas

Jetpack Compose中的Canvas

Jetpack Compose中的Canvas API 使用起来感觉比传统View中的要简单一些&#xff0c;因为它不需要画笔Paint和画布分开来&#xff0c;大多数直接就是一个函数搞定&#xff0c;当然也有一些限制。 Compose 直接提供了一个叫 Canvas 的 Composable 组件&#xff0c;可以在任何 Co…
阅读更多...
containerd环境下build镜像

containerd环境下build镜像

containerd环境下build镜像安装nerdctl使用nerdctl打包docker镜像下载安装 buildkit编写systemd unit文件&#xff1a;启用buildkit.service并设置开机自动运行修改Dockerfile构建镜像containerd配置代理containerd配置代理ansible剧本安装nerdctl https://blog.csdn.net/omai…
阅读更多...
Python采集最热影评 + 制作词云图

Python采集最热影评 + 制作词云图

人生苦短&#xff0c;我用Python 电影评论&#xff0c;简称影评 是对一部电影的导演、演员、镜头、摄影、剧情、线索、环境、色彩、光线、视听语言、道具作用、转场、剪辑等进行分析和评论。 电影评论的目的在于分析、鉴定和评价蕴含在银幕中的审美价值、认识价值、社会意义、…
阅读更多...
Springboot中，异步线程的执行顺序的控制

Springboot中，异步线程的执行顺序的控制

1、顺序的定义异步任务存在如下几种顺序&#xff1a;顺序的开启子任务&#xff08;运行顺序和结束顺序不确定&#xff09;。顺序的完成&#xff08;就是A先启动&#xff0c;先执行完&#xff0c;再执行B任务&#xff0c;往往A、B之间存在某种依赖关系&#xff09;。还有就是优先…
阅读更多...
思科设备-配置静态路由

思科设备-配置静态路由

⬜⬜⬜ &#x1f430;&#x1f7e7;&#x1f7e8;&#x1f7e9;&#x1f7e6;&#x1f7ea; (*^▽^*)欢迎光临 &#x1f7e7;&#x1f7e8;&#x1f7e9;&#x1f7e6;&#x1f7ea;&#x1f430;⬜⬜⬜ ✏️write in front✏️ &#x1f4dd;个人主页&#xff1a;陈丹宇jmu &a…
阅读更多...
【云原生进阶之容器】第四章Operator原理4.2节--CRD

【云原生进阶之容器】第四章Operator原理4.2节--CRD

1 CRD概述 1.1 CRD简介 CRD全称是CustomResourceDefinition，在Kubernetes 中一切都可视为资源，Kubernetes 1.7 之后增加了对 CRD 自定义资源二次开发能力来扩展 Kubernetes API，通过 CRD 我们可以向 Kubernetes API 中增加新资源类型，而不需要修改 Kubernetes 源码来创建自…
阅读更多...
Django搭建个人博客Blog-Day03

Django搭建个人博客Blog-Day03

对user模块进行开发设计数据表Django默认就提供了和用户相关的功能&#xff0c;但是这个Django默认提供的功能有个不好的点: 不太适合我们的项目&#xff0c;例如里面的字段不够等&#xff0c;所以我们要对它进行改造一下&#xff0c;方便项目开发。拓展用户模型进入虚拟环境安…
阅读更多...
java1算法

java1算法

排序–comparable接口 java提供了一个接口Comparable用来定义类的排序规则 eg: 1、定义一个学生类Student&#xff0c;具有年龄age和姓名username连个属性&#xff0c;并通过Comparable接口提供比较规则&#xff1b; 2、定义测试类Test,在测试类中定义测试方法Comparable getM…
阅读更多...
还不会用YakitBp?来，我教你

还不会用YakitBp?来，我教你

前言 &#x1f340;作者简介&#xff1a;被吉师散养、喜欢前端、学过后端、练过CTF、玩过DOS、不喜欢java的不知名学生。 &#x1f341;个人主页&#xff1a;被吉师散养的职业混子 &#x1f342;相应专栏&#xff1a;CTF专栏 Yakit介绍 好兄弟&#xff0c;你听说过yakit吗&…
阅读更多...
Redis五大基本数据类型

Redis五大基本数据类型

Redis五大基本数据类型 1.Redis通用命令 常用命令 #Redis的键key操作 keys * 表示查看当前库所有key 【注意是&#xff1a;可以使用通配符】 exists <key> 表示判断某个key是否存在&#xff0c;存在返回1&#xff0c;否则返回0 type <key> 表示判断key类型 del …
阅读更多...
fiddler的下载和安装，及常用操作

fiddler的下载和安装，及常用操作

目录 一、fiddler介绍 二、fiddler的下载和安装 三、fiddler的简单配置 四、fiddler的抓包 五、fiddler的自动响应器 六、fiddler的断点 七、fiddler的构造器 一、fiddler介绍 Fiddler是比较好用的Web代理调试工具之一&#xff0c;它能记录并检查所有客户端与服务端的HT…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023